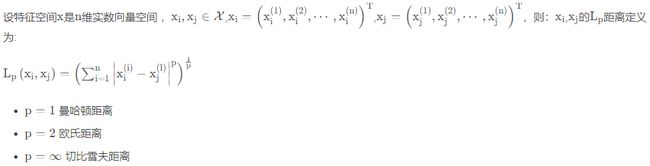KNN算法
文章目录
- 1. 什么是KNN算法
- 2. KNN算法原理
-
- 2.1 距离度量
- 2.2 交叉验证选取k值
- 2.3 分类决策规则
- 3. KNN算法特点及应用场景
- 4. KNN算法的Python应用
-
- 4.1 KNN算法的Python实现
- 4.2 sklearn.neighbors.KNeighborsClassifier(k近邻分类器)
- 5. 源码仓库地址
1. 什么是KNN算法
KNN(K Nearest Neighbors,又称k近邻法)是一种基本的分类和回归方法,是监督学习方法里的一种常用方法。
KNN算法通过距离判断两个样本是否相似,使用与未知样本最近的k个样本(近邻)的类别来分类,数量最多的标签类别就是新样本的标签类别。
2. KNN算法原理
KNN算法三要素:距离度量、k值的选择和分类决策规则。常用的距离度量是欧氏距离及更一般的pL距离。k值小时,k近邻模型更复杂,容易发生过拟合;k值大时,k近邻模型更简单,又容易欠拟合。因此k值得选择会对分类结果产生重大影响。k值的选择反映了对近似误差与估计误差之间的权衡,通常由交叉验证选择最优的k。分类决策规则往往是多数表决,即由输入实例的k个邻近输入实例中的多数类决定输入实例的类。
2.1 距离度量
一般采用二维欧氏距离。
2.2 交叉验证选取k值
在许多实际应用中数据是不充足的。为了选择好的模型,可以采用交叉验证方法。交叉验证的基本思想是重复地使用数据,把给定的数据进行切分,将切分的数据组合为训练集与测试集,在此基础上反复进行训练测试以及模型的选择。
2.3 分类决策规则
KNN使用的分类决策规则是多数表决,如果损失函数为0-1损失函数,那么要使误分类率最小即使经验风险最小,多数表决规则实际上就等同于经验风险最小化。
3. KNN算法特点及应用场景
KNN是一种非参的,惰性的算法模型。什么是非参,什么是惰性呢?
非参的意思并不是说这个算法不需要参数,而是意味着这个模型不会对数据做出任何的假设,与之相对的是线性回归(我们总会假设线性回归是一条直线)。也就是说KNN建立的模型结构是根据数据来决定的,这也比较符合现实的情况,毕竟在现实中的情况往往与理论上的假设是不相符的。
惰性又是什么意思呢?举例说,同样是分类算法,逻辑回归需要先对数据进行大量训练,最后才会得到一个算法模型。而KNN算法却不需要,它没有明确的训练数据的过程,或者说这个过程很快。
KNN算法优点:
(1) 简单易用,相比其他算法,KNN算是比较简洁明了的算法。即使没有很高的数学基础也能搞清楚它的原理。
(2)模型训练时间快。
(3)预测效果好。
(4)对异常值不敏感。
KNN算法缺点:
(1)对内存要求较高,因为该算法存储了所有训练数据。
(2)预测阶段可能很慢。
(3)对不相关的功能和数据规模敏感。
那么什么时候应该选择使用KNN算法呢?一般来说,当需要使用分类算法,且数据比较大的时候就可以尝试使用KNN算法进行分类了。
4. KNN算法的Python应用
4.1 KNN算法的Python实现
如下代码所示,通过提供训练集,包含A和B两类数据,预测测试数据属于哪一类:
import operator
import numpy as np
# trainData - 训练集,testData - 测试集,labels - 分类
def knn(trainData, testData, labels, k):
# 计算训练样本的行数
rowSize = trainData.shape[0]
# 计算训练样本和测试样本的差值
diff = np.tile(testData, (rowSize, 1)) - trainData
# 计算差值的平方和
sqrDiff = diff ** 2
sqrDiffSum = sqrDiff.sum(axis=1)
# 计算距离
distances = sqrDiffSum ** 0.5
# 对所得的距离从低到高进行排序
sortDistance = distances.argsort()
count = {}
for i in range(k):
vote = labels[sortDistance[i]]
count[vote] = count.get(vote, 0) + 1
# 对类别出现的频数从高到低进行排序
sortCount = sorted(count.items(), key=operator.itemgetter(1), reverse=True)
# 返回出现频数最高的类别
return sortCount[0][0]
trainData = np.array([[5, 1], [4, 0], [1, 3], [0, 4]])
labels = ['A', 'A', 'B', 'B']
testData = [3, 2]
X = knn(trainData, testData, labels, 3)
print(X)
很明显,测试数据属于A类,实际预测结果也为A类。
4.2 sklearn.neighbors.KNeighborsClassifier(k近邻分类器)
sklearn.neighbors.KNeighborsClassifier()函数是用于实现k近邻投票算法的分类器。其函数原型如下:
sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,weights=’uniform’, algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)
参数说明:
- n_neighbors:int,optional(default = 5)
默认情况下kneighbors查询使用的邻居数。就是k-NN的k的值,选取最近的k个点。
- weights:str或callable,可选(默认=‘uniform’)
默认是uniform,参数可以是uniform、distance,也可以是用户自己定义的函数。uniform是均等的权重,即所有的邻近点的权重都是相等的。distance是不均等的权重,距离近的点比距离远的点的影响大。用户自定义的函数,接收距离的数组,返回一组维数相同的权重。
- algorithm:{‘auto’,‘ball_tree’,‘kd_tree’,‘brute’},可选
快速k近邻搜索算法,默认参数为auto,可以理解为算法自己决定合适的搜索算法。除此之外,用户也可以自己指定搜索算法ball_tree、kd_tree、brute方法进行搜索,brute是蛮力搜索,也就是线性扫描,当训练集很大时,计算非常耗时。kd_tree,构造kd树存储数据以便对其进行快速检索的树形数据结构,kd树也就是数据结构中的二叉树。以中值切分构造的树,每个结点是一个超矩形,在维数小于20时效率高。ball_tree是为了克服kd树高纬失效而发明的,其构造过程是以质心C和半径r分割样本空间,每个节点是一个超球体。
- leaf_size:int,optional(默认值=30)
默认是30,这个是构造的kd树和ball树的大小。这个值的设置会影响树构建的速度和搜索速度,同样也影响着存储树所需的内存大小。需要根据问题的性质选择最优的大小。
- p:整数,可选(默认=2)
距离度量公式,默认使用欧氏距离公式进行距离度量。除此之外,还有其他的度量方法,例如曼哈顿距离。这个参数默认为2,也就是默认使用欧式距离公式进行距离度量。也可以设置为1,使用曼哈顿距离公式进行距离度量。
- metric:字符串或可调用,默认为’minkowski’
用于距离度量,默认度量是minkowski,也就是p=2的欧氏距离(欧几里德度量)。
- metric_params:dict,optional(默认=None)
距离公式的其他关键参数,使用默认的None即可。
- n_jobs:int或None,可选(默认=None)
并行处理设置。默认为1,临近点搜索并行工作数。如果为-1,那么CPU的所有cores都用于并行工作。
注意:如果发现两个邻居,邻居k+1和k具有相同距离但不同标签,则结果将取决于训练数据的排序。
测试代码如下:
from sklearn.neighbors import KNeighborsClassifier
X = [[5, 1], [4, 0], [1, 3], [0, 4]]
y = ['A', 'A', 'B', 'B']
neigh = KNeighborsClassifier(n_neighbors=3)
neigh.fit(X, y)
print(neigh.predict([[3, 2]]))
预测结果同样为A类。
5. 源码仓库地址
图像处理、机器学习的常用算法汇总