leetcode329. 矩阵中的最长递增路径(java)

矩阵中的最长递增路径

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/longest-increasing-path-in-a-matrix

题目描述

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。
对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例1：

输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4
解释：最长递增路径为 [1, 2, 6, 9]。

示例2：

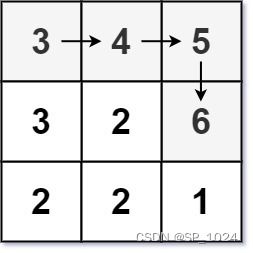
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：
输入：matrix = [[1]]
输出：1

提示：
m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
0 <= matrix[i][j] <= 231 - 1

暴力递归

每个位置，我们都要去计算其最大递归序列的长度，因此每到一个位置，我们就要去递归他上下左右四个位置的可能性，在递归的过程中要做好边界判断，不能越界。

代码演示

public int longestIncreasingPath(int[][] matrix) {

        int m = matrix.length;
        int n = matrix[0].length;
        //保存最大值
        int ans = 0;
       
        //遍历每个位置
        for(int i = 0; i < m;i++){
            for(int j = 0; j < n;j++){
                int p = process1(matrix,i,j);
                ans = Math.max(ans,p);
            }
        }    
        return ans;
    }
    /**
    * 暴力递归
    * i  和 j 是递归到的位置。
     */
    public int process1(int[][]m,int i,int j){
       
        //做好边界判断
        int up = i > 0 && m[i][j] < m[i - 1][j] ? process1(m, i - 1, j) : 0;
		int down = i < (m.length - 1) && m[i][j] < m[i + 1][j] ? process1(m, i + 1, j) : 0;
		int left = j > 0 && m[i][j] < m[i][j - 1] ? process1(m, i, j - 1) : 0;
		int right = j < (m[0].length - 1) && m[i][j] < m[i][j + 1] ? process1(m, i, j + 1) : 0;
        //四种方向上的最大值加上本身节点的，加1，就是最大递增子序列
        return Math.max(Math.max(up,down),Math.max(left,right)) + 1;
    }

递归 + 缓存

递归过程中有两个变量 i 和 j,我们用缓存保存起来，做到记忆化搜索，
这样节省大量重复计算。

代码演示

    public int longestIncreasingPath(int[][] matrix) {

        int m = matrix.length;
        int n = matrix[0].length;
        //保存最大值
        int ans = 0;
        //缓存表
        int[][]dp = new int[m + 1][n + 1];
        for(int i = 0; i < m;i++){
            for(int j = 0; j < n;j++){
                int p = process2(matrix,i,j,dp);
                ans = Math.max(ans,p);
            }
        }    
        return ans;
    }
  
		/**
		* 递归加缓存 
		*/
     public int process2(int[][]m,int i,int j,int[][]dp){
     	//缓存里直接从缓存里拿
          if(dp[i][j] != 0){
            return dp[i][j];
        }
        int up = i > 0 && m[i][j] < m[i - 1][j] ? process2(m, i - 1, j,dp) : 0;
		int down = i < (m.length - 1) && m[i][j] < m[i + 1][j] ? process2(m, i + 1, j,dp) : 0;
		int left = j > 0 && m[i][j] < m[i][j - 1] ? process2(m, i, j - 1,dp) : 0;
		int right = j < (m[0].length - 1) && m[i][j] < m[i][j + 1] ? process2(m, i, j + 1,dp) : 0;
		//结果放到缓存里
        dp[i][j] = Math.max(Math.max(up,down),Math.max(left,right)) + 1;
        return dp[i][j] ;
    }

动态规划专题

leetcode198. 打家劫舍

leetcode174. 地下城游戏

打败怪兽的概率

leetcode688. 骑士在棋盘上的概率

钱币的组合有多少种

最小路径和

最长回文子序列