leetcode算法 -- 数组
1 数组
常见的数组算法有双指针,滑动窗口,二分查找和分冶。
2 双指针
核心的思路:使用两个指针,一个从头开始索引,一个从尾开始索引。
2.1 两数之和ii 167
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/remove-duplicates-from-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:num1+num2=target;数组按照非递增顺序进行排列;
num1从最小的数开始,num2从最大的数开始,根据两数之和和target的关系,移动两个指针;
Algorithm TwoSum(nums, target):
Input: A list of numbers "nums" and a target number "target"
Output: A list of two indices
i <- 0
j <- length(nums) - 1
while j > i do // 没有重复元素
val <- nums[i] + nums[j]
if val > target then
j <- j - 1
else if val < target then
i <- i + 1
else
return [i, j]
return []
2.2 反转字符串中的元音字母 345
给你一个字符串 s ,仅反转字符串中的所有元音字母,并返回结果字符串。
元音字母包括 ‘a’、‘e’、‘i’、‘o’、‘u’,且可能以大小写两种形式出现不止一次。
用两个指针从头和尾开始索引
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/remove-duplicates-from-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
Algorithm ReverseVowels(strs):
Input: A string "strs"
Output: A string with its vowels reversed
i <- 0
j <- length(strs) - 1
while j > i do
while !findVowel(strs[i]) do
i <- i + 1
end while
while !findVowel(strs[j]) do
j <- j - 1
end while
swap(strs, i, j)
i <- i + 1
j <- j - 1
end while
return strs
2.3 移除元素 27
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/remove-element
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路1:头尾用两个指针,找到合适的,就发生交换,最后右指针的位置。
Algorithm MoveTargetToFront(nums, target):
Input: A list of numbers "nums" and a target number "target"
Output: An integer representing the final index 'j' incremented by 1
i <- 0
j <- length(nums) - 1
while j > i do
if nums[i] == target then
swap(nums, i, j)
i <- i + 1
j <- j - 1
else
i <- i + 1
end if
end while
return j + 1
2.4 删除重复元素
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/remove-duplicates-from-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:用指针i,迭代索引数组,用指针k从0开始记录没有重复的数据
Algorithm MoveTargetToFront(nums, target):
Input: A list of numbers "nums" and a target number "target"
Output: An integer representing the final index 'j' incremented by 1
k <- 1
pre = INT_MIN // 一个技巧,防止首数字重复
for i <- 0 to n - 1 do
if nums[i] != pre then
nums[k] <- nums[i]
pre = nums[i]
k <- k + 1
endif
endfor
return k
2.5 三数之和 (3Sum) 15
给你一个整数数组 nums ,判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ,同时还满足 nums[i] + nums[j] + nums[k] == 0 。请
你返回所有和为 0 且不重复的三元组。
注意:答案中不可以包含重复的三元组。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/3sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:将三数之和转换成两数之和,然后在用两个指针,一左一右进行迭代搜索。
for i <- 0 to n - 3 do
if nums[i] > 0 then
break
endif
j <- i + 1
k <- n - 1
while k > j do
if nums[i] + nums[j] + nums[k] > 0 then
k <- k - 1
else if nums[i] + nums[j] + nums[k] < 0 then
j <- j + 1
else if nums[i] + nums[j] + nums[k] == 0 then
result.push_back({i, j, k})
j <- j + 1
k <- k - 1
// 有重复的内容,进行迭代更新
while nums[j] == nums[j - 1] do
j <- j + 1
while nums[k] = nums[k + 1] do
k <- k - 1
endif
endwhile
endfor
2.6 盛最多水的容器11
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/container-with-most-water
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
left <- 0
right <- n - 1
max_area <- 0
while right > left do
area <- (right - left) * max(nums[left], nums[right])
if area > max_area then
max_area <- area
endif
if nums[left] > nums[right] then
right <- right - 1
else
left <- left + 1
endif
endwhile
return max_area
2.7 两数之和 (Two Sum)1
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/two-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路1:先将nums按照递增进行排序,然后用左右两个指针;
思路2:通过unordered_map
2.8 反转字符串 II (Reverse String II) 541
给定一个字符串 s 和一个整数 k,从字符串开头算起,每计数至 2k 个字符,就反转这 2k 字符中的前 k 个字符。
如果剩余字符少于 k 个,则将剩余字符全部反转。
如果剩余字符小于 2k 但大于或等于 k 个,则反转前 k 个字符,其余字符保持原样。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/reverse-string-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:将 i ∈ [ 0 , k − 1 ] i \in [0,k-1] i∈[0,k−1] 进行reverse; i ∈ [ k , 2 k − 1 ] i \in [k, 2k-1] i∈[k,2k−1]不进行调整;
// 通过step: 2k,防止最后一段处理不了
for i <- 0 to n - 1 step 2k do
reverse(str.begin() + i, str.begin() + i + min(k, n - 1 - i))
endfor
2.9 回文字符串 II (Valid Palindrome II)680
给你一个字符串 s,最多 可以从中删除一个字符。
请你判断 s 是否能成为回文字符串:如果能,返回 true ;否则,返回 false 。
思路:
通过递归来处理,check(s, i, k, time),不仅可以处理删除一个,可以处理删除k个
bool ValidPalindrome(s)
result = check(s, 0, n-1, 1) // 可以错误一次
return result
bool check(s, i, j, time)
while (i < j)
if (s[i] != s[j])
return time > 0 || check(s, i, j-1, time--) || check(s, i + 1, j, time--)
endif
i++
j--
endwhile
3 滑动窗口
滑动窗口(Sliding Window)是一种常见的算法策略,主要用于解决数组/链表的子元素问题,如求解子数组的最大和、子数组的最小长度等。
Algorithm SlidingWindowAlgorithm(arr, target):
Input: An array of integers arr, and a target integer target
Output: The desired subarray or length or sum etc.
left <- 0 // initialize left pointer
right <- 0 // initialize right pointer
windowSum <- 0 // initialize the sum of the window
minLength <- inf // initialize the length of the minimum subarray
result <- []
while right is less than length of arr do:
// expand the right boundary of the window
windowSum <- windowSum + arr[right]
right <- right + 1
// shrink the window from the left
while windowSum is greater than target do:
minLength <- min(minLength, right - left)
windowSum <- windowSum - arr[left]
left <- left + 1
if windowSum equals to target then
result.push(subarray from left to right-1)
windowSum <- windowSum - arr[left]
left <- left + 1
return result or minLength
3.1 最大子序和 (Maximum Subarray) 53
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
思路:技巧:如何累加的结果比0小,那么就重新开始累加
Algorithm MaximumSubarraySum(nums):
Input: An array of integers nums
Output: Maximum subarray sum
res <- 0 // initialize the current subarray sum
sum <- 0 // initialize the maximum subarray sum
// 处理特殊情况,如果最大的数没有0大怎么办
res <- INT_MIN
for i from 0 to n-1 do:
res <- max(res, nums[i])
endfor
if res <= 0 then
return res;
endif
for i from 0 to n-1 do:
res <- res + nums[i]
res <- max(0, res)
sum <- max(sum, res)
endfor
return sum
3.2 和为K的子数组 (Subarray Sum Equals K) 560
思路:将和存在unordered_map
um <- unordered_map<int, int>()
sum <- 0
um[0] <- 1
count <- 0
for i from 0 to n-1 do
sum <- sum + nums[i]
if um.find(sum - target) != um.end() then
count <- count + um[sum - target]
um[sum] <- um[sum] + 1
endfor
3.4 长度最小的子数组 (Minimum Size Subarray Sum) 209
思路:这里有个技巧,找到长度最小的子数组后,继续往后搜索
l_sum
r_sum
min_len = n - 1
for i from 0 to n-1 do
r_sum <- r_sum + nums[i]
while r_sum - l_sum < k do
if (j - r + 1 < min_len) then
min_len = r - l + 1
endif
l_sum <- l_sum + nums[j++]
endwhile
endfor
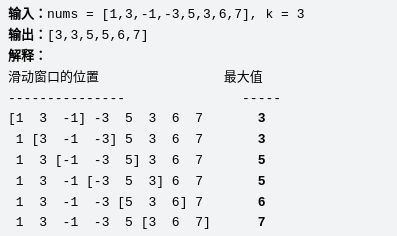
3.5 滑动窗口最大值 (Sliding Window Maximum) 239
思路:
1)通过map得到最大值;
map.rbegin()->first
2)通过++um[num[i]]进行滑动记录,删除不需要的内容
map<int, int>um;
int k = min(n, k)
for i from 0 to k-1 do
++um[nums[i]];
endfor
res.push_back(um->rbegin()->first)
for i from k to n - 1 do
if --um[i - k] == 0 then
um.erase(nums[i - k])
endif
++um[i];
res.push_back(um->rbegin()->first)
endfor
3.6 无重复字符的最长子串 3
给定一个字符串 s ,请你找出其中不含有重复字符的 最长子串 的长度。
关键的是要实时更新最左边的数据
unordered_map<char, int> um
max_len <- 0
l <- 0
for r from 0 to n-1 do
if um.find(s[r]) != um.end() then
if um[s[r]] >= l then
l <- um[s[r]] + 1
endif
len <- r - l + 1
if len > max_len then
max_len <- len
endif
endif
um[s[r]] = r
endfor
3.8 和为K的最长子数组长度1493
给你一个二进制数组 nums ,你需要从中删掉一个元素。
请你在删掉元素的结果数组中,返回最长的且只包含 1 的非空子数组的长度。
如果不存在这样的子数组,请返回 0 。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-subarray-of-1s-after-deleting-one-element
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
使用两个指针,l 从左边迭代到最右边,r 遇到两次0停下来, l 从零开始
for l from 0 to n-1 do
cnt <- 0
while s[r++] == '0' then
cnt <- cnt + 1
endwhile
while cnt > 1 then
if s[r++] == '0'
cnt <- cnt - 1
endwhile
max_len <- max(max_len, r - l - 1)
endfor
3.9 连续的子数组和 523
给你一个整数数组 nums 和一个整数 k ,编写一个函数来判断该数组是否含有同时满足下述条件的连续子数组:
子数组大小 至少为 2 ,且
子数组元素总和为 k 的倍数。
如果存在,返回 true ;否则,返回 false 。
如果存在一个整数 n ,令整数 x 符合 x = n * k ,则称 x 是 k 的一个倍数。0 始终视为 k 的一个倍数。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/continuous-subarray-sum
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
两个相同部分的余数相减的结果是K的倍数。
unordered_map<int, int> um;
sum <- 0
for i from 0 to n-1 do
sum <- (sum + nums[i]) % k
if um.find(sum) != um.end() then
return tru;
endif
um[sum] = i
endfor
return false
3.10 替换后的最长重复字符 424
给你一个字符串 s 和一个整数 k 。你可以选择字符串中的任一字符,并将其更改为任何其他大写英文字符。该操作最多可执行 k 次。
在执行上述操作后,返回包含相同字母的最长子字符串的长度。
来源:力扣(LeetCode)
链接:https://leetcode.cn/problems/longest-repeating-character-replacement
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
思路:
1)r从0到n-1开始迭代,每次迭代过程中,找到合适的l,满足要求。如果大于要求,就去迭代更新了.
2)用前缀的unordered_map记录字符出现的次数
unordered_map<int, int> um
for r from 0 to n-1 do
++um[nums[r] - 'A']
int maxIndex = (std::max_element(um.begin(), um.end())
if r - l + 1 - um[maxIndex] > k then
--um[s[l++] - 'A']
endif
if r- l + 1 > max_len then
max_len <- r - l + 1
endif
endfor