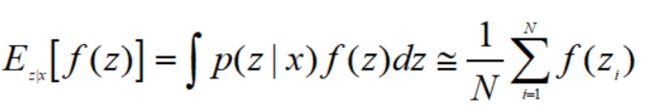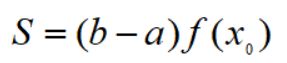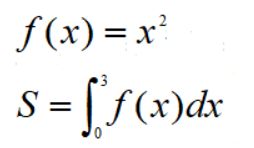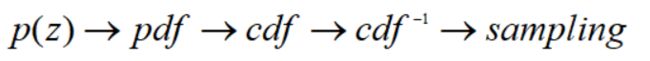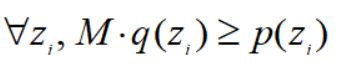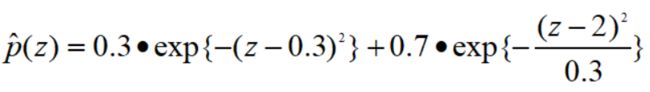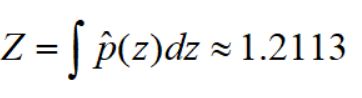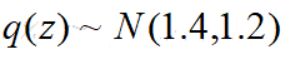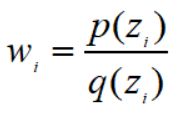MCMC(蒙特卡洛采样)
1.MCMC是一种随机性近似推断方法,核心思想是求复杂概率分布下的期望值
2.采样的样本应该趋于高概率区域以及样本之间相互独立
3.如果p(z)分布简单,可以通过概率分布采样得到所需要的样本
4.大多情况下,归一化因子无法求解和维度灾难的问题,无法直接得到p(z)分布
5.需要近似的方法去求解期望,主要借助蒙特卡洛随机近似思想
6.常用的蒙特卡洛采样方法有拒绝采样、重要性采样和MCMC
7.拒绝采样主要通过提议分布逼近复杂概率分布p(z)得到采样点
8.重要性采样直接对期望采样,可以解决原分布难采样的问题
马尔科夫链蒙特卡洛方法,英文是Markov Chain Monte Carlo,简称MCMC。是一种随机性近似推断方法,它也是求解隐变量后验分布的一种推断方法,核心思想是求复杂概率分布p(z)下对函数f(z)的期望值:
也就是用N的样本均值作为期望值。问题就转化为尽量保证采集的N个样本能反映总体。也就是如何进行采集更加合理。
要理解MCMC,得了解蒙特卡洛和马尔可夫链,这一节小编先介绍蒙特卡洛近似方法。
蒙特卡洛方法
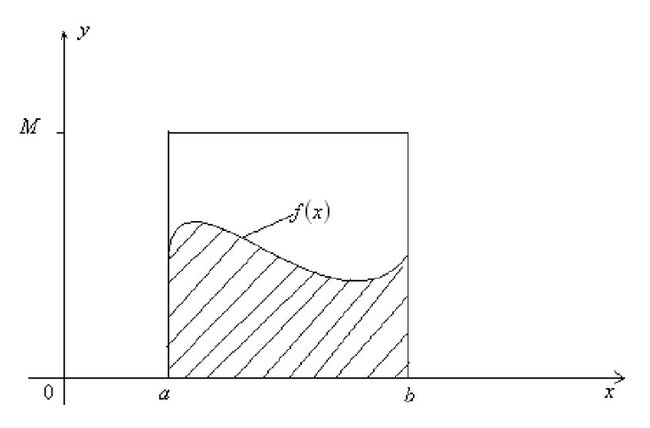
蒙特卡洛方法(Monte Carlo)是一种随机模拟的方法。最早的蒙特卡洛方法都是为了求解一些不太好求解的求和或者积分问题,比如下面的积分:
一个简单的近似求解方法是在[a,b]之间随机的采样一个点,然后做积分
但一个样本点比较粗糙,可以在[a,b]之间随机采样n个值,然后取均值:
这样子依然存在一个问题,那就是假定x在[a,b]之间是均匀分布的,但大多数情况并非如此,于是,提出改进方案:
红框就是蒙特卡洛的一般形式。我们举一个例子来理解这个过程。
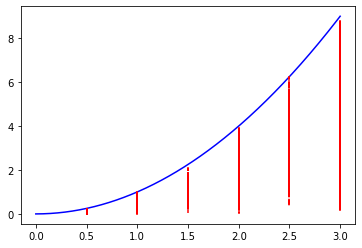
要求解二次函数在[0,3]上的积分:
采取牛顿莱布尼茨方法很容易求解结果是9,现在假设我们用蒙特卡洛方法来求解该积分,也即红色区域的面积:
按照蒙特卡洛方法,我们采样n次,p(x)定义为[0,3]的均匀分布,于是编写代码:
li = []
for n in [100,500,1000,5000,10000,50000,100000,500000,1000000]:
s = 0
for i in range(n):
a = random.uniform(0,3) #在p(x)采样
f = fun(a) #f(x)
s += 3*f #sum[f(x)/p(x)]
li.append([n,s/n])
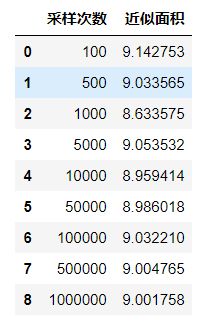
pd.DataFrame(li,columns=['采样次数','近似面积'])
看看结果
可见,蒙特卡洛近似值与实际值接近。
实际上,蒙特卡洛是一种近似思想,其具体实现过程有很多,核心是求解x的概率分布p(x),以及如何基于概率分布去采集n个样本点。
在正式介绍具体采样方法前,先对采样做一个整体了解。
采样整体介绍
对于采样任务来说,它的动机一般有两种:
-
采样作为任务,用于生成新的样本
-
求和/求积分
第一个很容易理解,比如要储存一组服从高斯分布的样本,我们只需要存储均值与方法,在特点场景再随机生成一些样本即可;第二个就是前一节提到的,主要用于近似求期望,也即积分问题。
采样后,我们想知道这些样本是否可以代表总体,也就是采集的样本是不是好的样本,评价标准有两个:
-
样本趋向于高概率的区域
-
样本之间必须独立
具体的采样过程中,也会遇到困难:
-
无法采样得到归一化因子
-
如果归⼀化因子可以求得,但是对高维数据依然不能均匀采样(维度灾难)
如果求解复杂的概率分布,那么需要做归一化处理:
归一化因子Z一般求解不出来,所以面对复杂的情况也无法直接采样。面对高维空间的样本,状态空间呈现指数级的形式,直接采样也是不可行的。
这时候需要借助蒙特卡洛方法,主要有拒绝采样、重要性采样和MCMC。我们这一节详细介绍前两种
采样方法
常用的有三种:概率分布采样(CDF Sampling)、拒绝采样(Rejection Sampling)和重要性采样(Importance Sampling)。
-
概率分布采样
这种方法适用于已知p(z)的分布情况下采样,比如前面提到的均匀分布,还有高斯分布、t分布等,都可以用该采样方法采样。它的采样思路是通过CDF的反函数采样:
如果z不是常见的分布,也即求解不出cdf,该方法不可用。
-
拒绝采样
对于复杂的概率分布p(z),引入已知的提议分布(proposal distribution)q(z),使得
其中,M为常数。
我们在q(z)进行采样,如果样本点落在黑色区域部分,则接受这个样本,如果落在红色区域,则拒绝这个样本。定义接收率α:
注:p(z)用的是未归一化的形式,因为通常情况归一化因子Z无法求解
采样算法为:
我们举一个例子来理解这个过程。
假设z的概率密度形式为:
其归一化因子用计算机可以解得(通常无法求解):
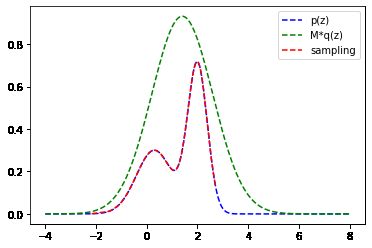
其分布形式可视化:
很显然,我们要基于该分布形式直接采样不现实,引入提议分布q(z):
即高斯分布进行拒绝采样,取常数M=2.8。编写代码如下:
from scipy.stats import norm
sampling_li = [] #用于接收采样样本
qz_li = norm.rvs(loc=gassi_u,scale=sigma,size=100000) #生成提议函数一系列样本
for n in range(1000):
z = random.choice(qz_li) #取q(z)的一个样本
a = fun(z)/(M*norm.pdf(z,gassi_u,sigma)) #计算接收率
u = random.uniform(0,1) #均匀分布采样
if u <= a:
sampling_li.append(z)
else:
continue
我们看看采样样本的分布
可见,样本来自高概率区域。
-
重要性采样
求解复杂概率分布p(z)下f(z)的期望值,除了拒绝性采样,还有一种直接对期望进行采样的方法——重要性采样:
![]()
红框部分就是样本的权重:
最终f(z)的期望值转化为q(z)分布下对函数f(z)p(z)/q(z)的期望。
重要性采样有两个作用,第一解决原分布难采样的问题,第二改进原分布.
举个例子:
如果我们直接从分布p(x)采样,而实际这些样本对应f(x)都很小,采样有限的情况下很有可能都无法得f(x)值比较大的样本;而如果我们找到一个分布q(x),使得它能f(x)*p(x)较大的地方采集到样本,则能更好地逼近我们的期望,而因为有重要性权重来控制新分布的比重,所以结果也不会偏差.
参考资料:
《概率图模型原理与技术》
https://www.cnblogs.com/pinard/p/6625739.html
https://mp.weixin.qq.com/s/ZyH_9EBXYaDJxSvVgUaNew