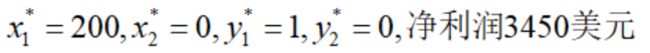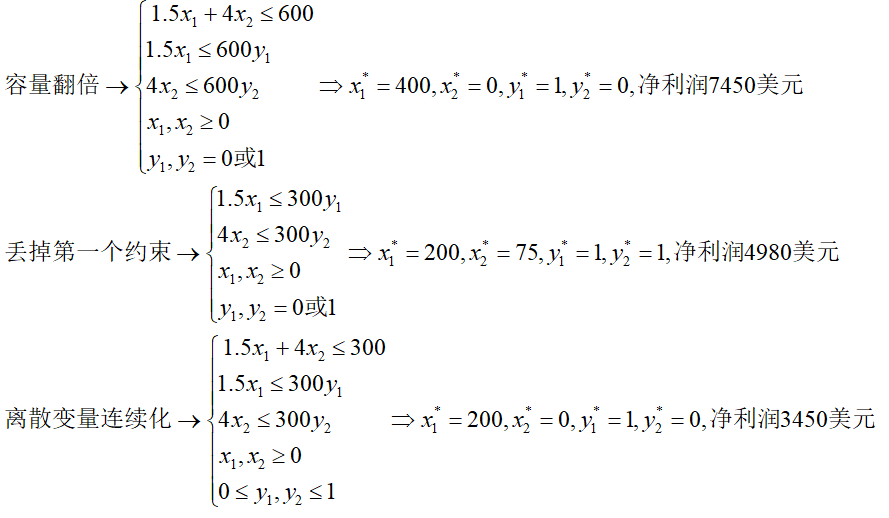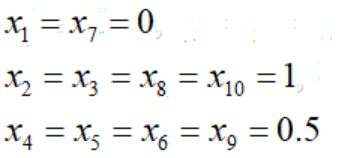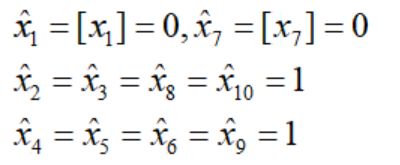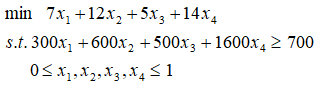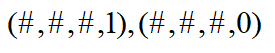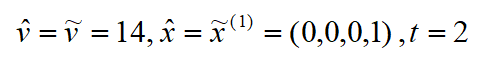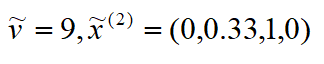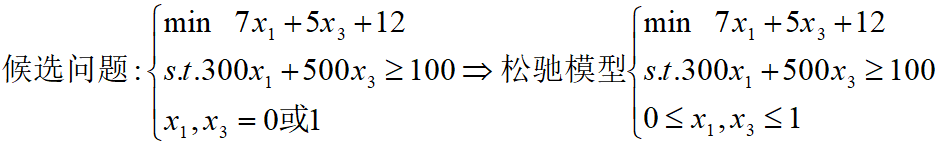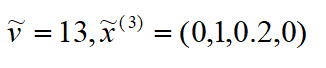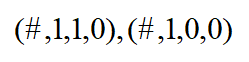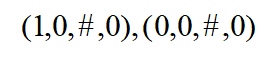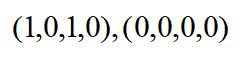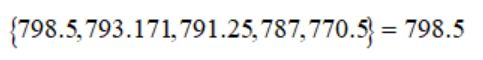离散优化的精确求解方法

在上一篇我们列举了各式各样的整数与组合规划模型。一些是含离散约束的线性规划，一些是含整数变量的线性规划，还有一些是连续与整数组合的非线性规划。这些模型的求解方法也极为丰富，今天我们介绍精确优化（exact optimal）方法。

传送门：离散优化模型

1

全枚举法求解

如果一个模型只有少数离散变量，最有效的求解方法往往也是最直接的：列举出所有可能。这个称为全枚举法（total enumeration），它尝试离散变量取值的所有组合，计算出任何连续变量在每种情形下的最佳对应取值来解决离散优化问题。

比如瑞士钢铁“全或无”的案例中：

这个案例中，只有两个离散决策变量，前后只需要跑四次线性规划模型即可。要是遇到指数级增长的离散变量，该方法显然不再是一种可以考虑的途径。

2

松弛模型

松弛模型（relaxation）通过寻找与离散优化模型相关但更简单的建模来解决原问题，在给定的离散模型中，松弛模型要么削弱约束，要么削弱目标函数，或者同时削弱两者。

案例：野牛助力者

野牛助力者俱乐部支持他们正决定在下一个地区展会时采用什么方式为当地运动队筹款，一个选择是个性定制T恤衬衫，每件卖20美元；另一个选择是卖运动衫，每件30美元。历史数据表明，展销品都将在展会结束前卖光。

制作衬衫的材料都是当地商人捐赠，但是助力者必须租借定制用的设备。用来制作T恤衫的设备在展会期间的租用价格为550美元，制作运动衫的设备租价为720美元。展示空间也是需要考虑的另外一点。在展会上，助力者只有面积为300平方英尺的墙作为展示空间。每件T恤衫会占用1.5平方英尺，而每件运动衫会占用4平方英尺。那么，哪个计划将产生最大的净利润呢？

根据以上场景，转化为离散优化模型：

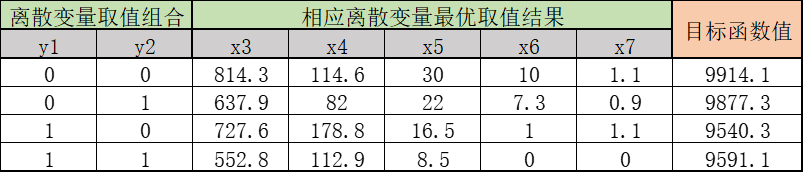
利用全枚举法，容易得到最优解为：

下面我们对约束条件进行放松，看看最优解的变化，以下列出了三种情况：

松弛模型应该遵循比原模型更易处理的原则，这样会让更加深入的分析变得可行。根据此，容量翻倍不满足要求，因为模型特征没有改变。第二个松弛更有效一点，因为解除了两种衬衫生产决策的联系。

第三种情况刻画了所有约束条件的松驰中最著名并且最常用的一种——线性规划松弛（linear programming relaxation），又称连续松弛（continuous relaxation）：

连续松弛是一种约束条件的松弛：保留所有其他约束，但将任何离散变量都看成连续变量

并非所有松弛都是对约束条件的放松，有时候目标函数也会被弱化。我们定义一个完整的松弛模型：

对于优化问题(R)和优化问题(P)，如果满足(i)每一个P的可行解在R中也都可行，并且(ii)P中每个可行解在R中的目标值与其在P中的目标相比都相等或更好，那么优化问题R是优化问题P的松弛

用数学符号表达就是：

进一步，我们有结论：如果一个松弛是不可行的，那么它的原模型也是不可行的

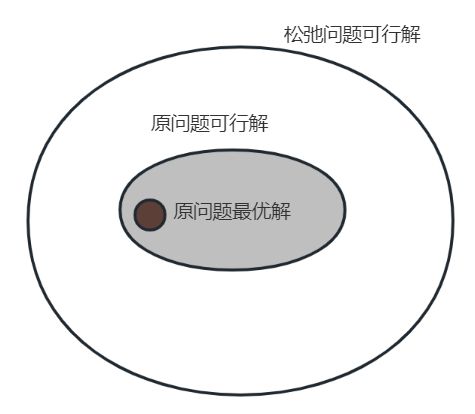
下面韦恩图展示了原问题与松弛问题的可行解关系：

注意，松弛模型提供了原问题最优解的确界（最大值问题是上界，最小问题是下界）。比如EMS模型，如果把离散变量全部改为连续变量获得松弛模型，利用单纯形法很容易得到一个最优解：

其最优值是6，换句话说，原问题至少需要6个EMS物流站才能满足需求。

我们想探讨什么情况下松弛模型能给出原问题的最优解，有结论：

如果一个约束条件松弛模型的最优解在原模型中也可行，那么这个解就是原模型的最优解

这个结论并不难得出，以前我们在机器学习讲解对偶问题的时候推导过，逻辑一致，这里不再赘述。

但从EMS案例可以看到，松弛最优解可能并非原模型的可行解，违反实际模型的一些约束。然而我们并非一无所获，从松弛模型我们得到了原模型的界，这样就拥有了一个起始点来建立针对原模型的启发式解。

比如EMS的松弛模型最优解中，我们要得到原模型的启发解，只需要对不满足离散的变量取整即可（向上取整或向下取整取决于约束条件，取整后满足可行性），EMS中，约束条件都是大于等于号，因此向上取整依然满足约束，于是得到启发解：

启发式最优解不一定是最优解，但它一定满足约束条件。有时候对于要求不那么精确的场景，用启发式最优解是一种高效的方法。

3

分支定界搜索

全枚举法对于绝大多数模型是不太可行的，但我们把这些解分成部分或枚举策略子集进行处理，结合松弛模型，可以得到分支定界算法（branch and bound algorithm）

该算法通过迭代的方法对一个解序列进行搜索，直到我们确认得到最优解，或停下以目前为止得到的最佳完整模型的可行解近似作为最优解。

我们用案例进行详细介绍——河流能源公司。

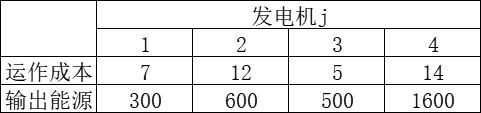
河流能源有4个发电机目前可用于生产，并且希望决定运行哪些发电机来满足未来几个小时预期的700兆瓦的尖峰需求。下表显示了运行每个发电机需要的成本（单位：千美元/时）和它们的输出能力（单位：兆瓦）。

我们把它看成背包问题：

通过枚举法可以得知，模型最优解为x1=x3=1,x2=x4=0，最低成本为12000美元

分支定界法通过部分解（partial solution）进行搜索，所谓部分解就是固定一些不变的决策变量，和其他自由或不确定的决策变量（用#表示），每个部分解都隐含定义了一类完全解，这些解叫做部分解的完全形式（completion）

比如能源河流案例，x=(1,#,0,#)描述了一个部分解，x2和x4是自由变量。该部分解的完全形式如下：

（1，0，0，0），（1，0，0，1），（1，1，0，0），（1，1，0，1）

其中后面三个被称为可行的完全形式（feasible completion），因为满足模型的全部约束。

进一步，我们把部分解中固定变量对应的受限模型（即自由变量所构成的模型）称为候选问题（candidate problem），我们利用候选问题的松弛问题来得到候选问题的启发解。

于是，我们得到基于线性规划的分支定界法（0—1整数规划）：

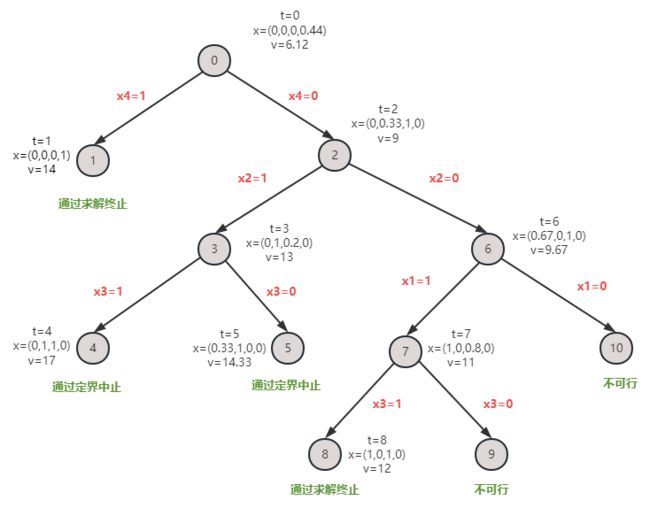
我们通过能源河流案例来理解这个算法，执行该算法的分支树为：

t=0，令所有变量为自由变量，即部分解为与目标值为:

其候选问题即为原问题，对应松驰模型为：

利用内点法求解最优值，得到：

进入到步骤5，最优解不满足所有二元约束(分量x4为分数），进入步骤6进行分支。

首先固定分量x4=0和x=1，得到两个活跃解:

回到步骤1，先看第一个，对应候选问题及候选问题的松驰模型为：

松驰模型最优解:

满足模型所有二元约束，该解为部分解的最优可行完全形式，更新最佳解:

此时通过求解终止，打上标签。回到步骤1，看第二个活跃解，写出相应候选问题与松驰模型：

最优解为：

再进行分支，产生两个活跃解(此时t=3):

回到步骤1，第一个活跃解对应的候选问题与松驰模型为：

最优解为：

再次进行分支（注意上面还有一个活跃解，待会不要遗漏），新的活跃解为：

此时t=4，回到步骤1，只剩下一个自由变量，第一个活跃解得到很容易得到最优解为17，大于最佳解14，通过步骤4定界终止。同样的第二个活跃解的最优解为14.3，同样是步骤4定界终止。

此时t=6，回到活跃解(#,0,#,0），得到最优解9.67,继续分支，得到活跃解：

第二个活跃解无法满足约束条件，不可行。只需要看第一个活跃解，最优解为11，继续分支，此时活跃解为：

最优值为12，已经不再有活跃解。迭代停止，并存在最优解(1,0,1,0）

这就是基于线性规划的分支定界法的逻辑。但这个过程还可以进行改良。其原理是：

分支定界搜索中每个不能被终止的部分解的松驰最优解通常在进行分支前取整，形成完整模型的可行解。如果这个可行解比其他已知解更好，那么它就提供了一个新的最佳解

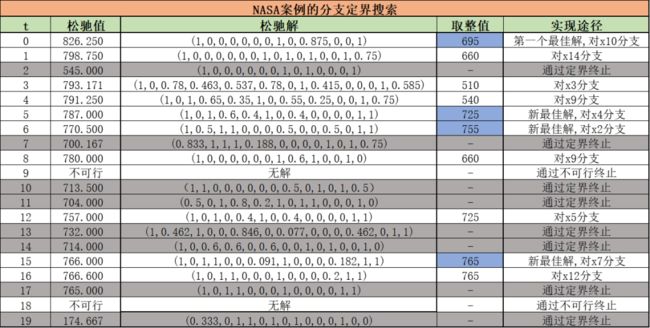
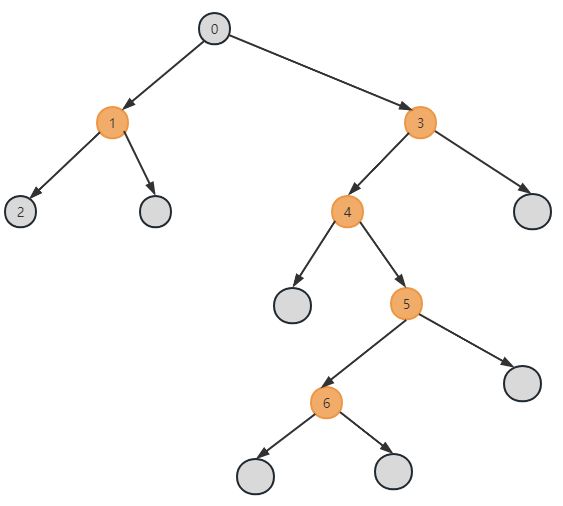
我们用上一篇的NASA资本预算案例进行说明，用分支定界法求解（深度向前最优回溯）该案例。得到如下的结果：

NASA案例中，需要向下取整（保证可行域）——即松驰最优解中的小数取值分量取0.比如在节点5的时候，候选问题的松驰最优解是787，按照算法逻辑应该进行下一步分支，但我们先取整得到取整解725，比最佳解大，此时更新最佳解为725.

因此我们只需要在步骤5与步骤6之间插入一步即可：

3

其他终止条件

上面展示了分支定界搜索算法整体一般逻辑，但其中还有一些终止问题需要进一步讨论。为了方便说明，我们需要引入一些术语：

任何一个直接从另一个节点通过分支得到的节点被称为子节点（child），被分支的节点则是母节点（parent）

根据分支原理，我们有母节点界限（parent boud）原理：对于一个求最小（大）值的模型，任何一个部分解所对应的母节点松驰最优值是这个子节点目标值的下（上）界

由此我们可以得到母节点界限终止的方法：当一个分支定界搜索找出了一个新的最佳解，对于任何一个还没有被终止的部分解，如果其母节点界限没有比新最佳解更优，那么这个部分解就可以马上被终止。

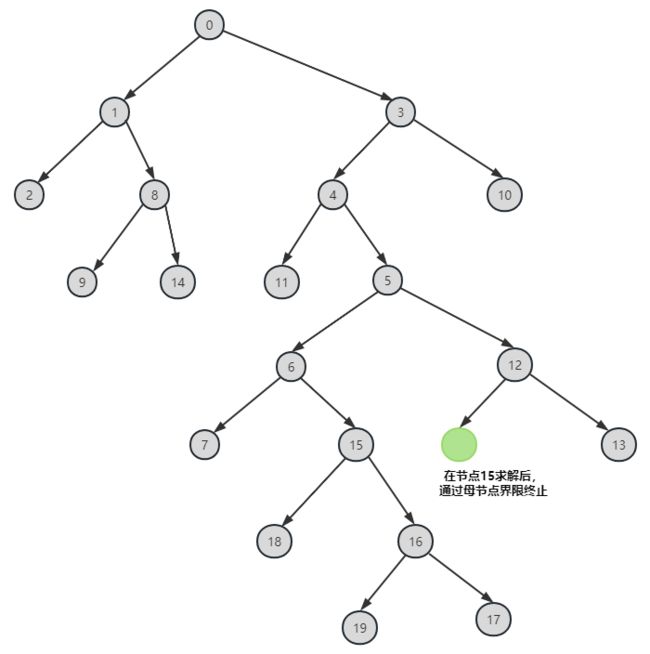
利用NASA案例的分支过程来介绍：

完成t=19后，搜索来到节点12的子节点，但此前已在节点15确定最优解765，而节点12的松驰最优解为757，因此可以立刻终止。

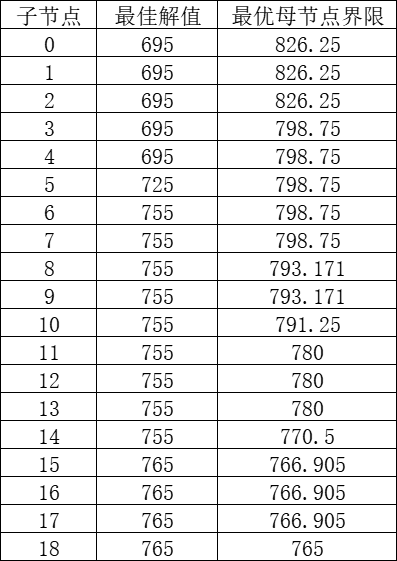
下表我们列出了子节点对应的最优母节点界限以及当前的最佳解：

最佳解很容易得到，这里要注意最优母节点界限的计算逻辑：是当前节点时刻活跃子节点的松弛解的界限，活跃节点是指当前节点时刻还没分支完成的节点

举个例子，对于节点6，要计算其最优母节点界限，首先在树形图中找到所有活跃子节点——1，3，4，5，6，这些节点的松弛解的界限为（最大值模型是上界）：

根据迭代最佳解与最优母节点界限可以得到提前停止（stop early）的启发：

在分支定界搜索中的任何一个阶段，任何活跃部分解的最佳解值和最优母节点界限之间的差，代表着我们接受最佳解作为一个近似最优解的最大误差

比如NASA案例，在t=6时刻得到的最佳解755，此时最优母节点界限为798.75（这个可能是最优的最佳解），我们计算其误差：

在t=16时刻，这个误差已经相当小了。有时候为了提高计算效率，我们只需要迭代通常的少量次数就能得到可以接受的近似解。这是提前停止的必要前提。

以上，我们基本把定界搜索涉及到算法细节（包含取整等）和终止条件（不可行终止、定界终止、求解终止、母节点界限终止和提前停止）介绍明白。但这里还有一个重要问题需要讨论，就是算法步骤1如何选取一个活跃解（存在多个活跃解前提下）进行迭代探索。

4

深度优先、最优优先和深度向前最优回溯

河流能源公司案例是利用深度优先（depth first）原则：在每一个循环处选择一个具有最多部分固定的活跃部分解

NASA案例则是利用深度向前最优回溯（depth forward best back）原则：在一个节点分支后选择最深的活跃部分解，但在终止了一个节点后选择具有最优母节点界限的活跃部分解

除此之外，还有利用最优优先（best first）原则：在每一个循环阶段，选择具有最优母节点界限的活跃部分解

采取这些原则进行迭代时，面对部分解还不唯一的情况，遵循下面统一的原则——最近子节点（nearest child）原则：

当最深或者具有最优母节点界限的部分解不唯一时，选择具有最后固定的变量值，且离母节点线性规划松驰的相应分量取值最接近的子节点部分解。

下面我们利用python实现三种优先原则的分支定界法，并且在NASA案例上来对比结果。

我们展示深度向前最优回溯的结果：

上表每一行记录了每个节点的信息，包括它的母节点，当下固定的变量，以及松驰解和状态。在节点17得到了最优解。

对于分支定界搜索算法，还可以在分支前寻找有效不等式再求解松驰模型，这延申为分支切割法。我们这里不再介绍了。以后有机会再补充吧。

代码开发附录：

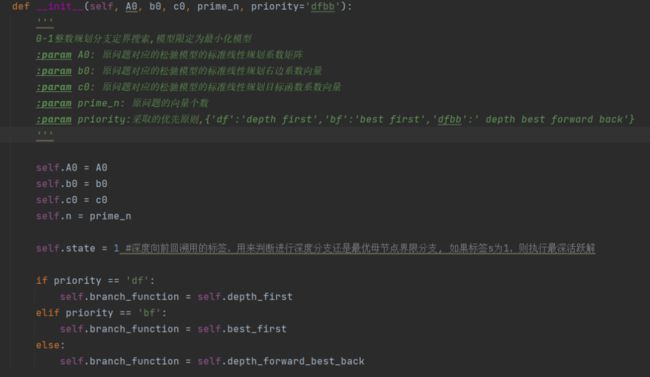
这里开发总体思路是用一张表，记录每个节点的信息。包括，节点，母节点，该节点固定的变量，松驰解、松驰值、取整解和最佳解等，然后用一个字段“状态”动态更新该节点是否进行分支、终止等信息，并记录分支的次数（最多2次）。每次循环用一个函数去更新里面的信息：

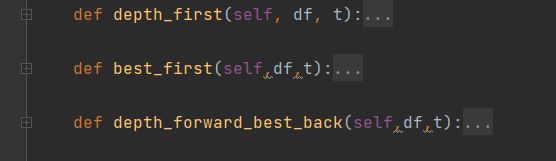
然后写三种分支原则的函数，用参数priority进行接收，分别指向三个不同原则的函数。由于原问题一般是不等式约束，但以前我们开发过的算法（单纯形等）都是基于标准型线性规划，因此，初始化方法传入的是化为原问题松驰模型的标准型线性规划的系数矩阵、右边系数向量和目标系数向量，然后用一个可传参数prime_n来声明原问题的变量个数。只不过计算过程只看原问题参数即可。

因为深度优先向前回溯中有最优优先，因此用参数state来控制是否执行最优优先。

接下来，要注意几个细节，就近子节点原则和最优母节点界限终止原则，用两个函数编写

最后编写主函数进行循环即可。注意里面的细节。

这里还要有一个函数去执行每一次线性规划的解，我们用以前开过的单纯形法，并把每次确认初始基的人工方法加入进去，自动执行单纯形法一阶段和二阶段。这里用内点法也可以，不过该算法要求初始基的每个分量都得大于0，通过求解线性方程组的通解去配一个都大于0的解可能需要一个高效的程序。由于单纯形法的人工阶段是找到线性无关组，用代码很容易实现。因此选择了单纯形法。