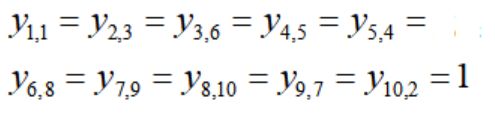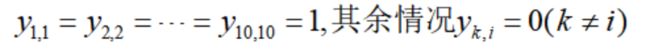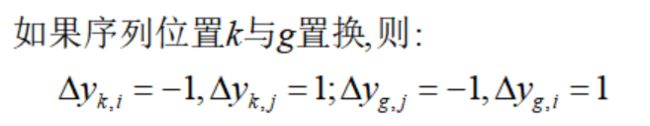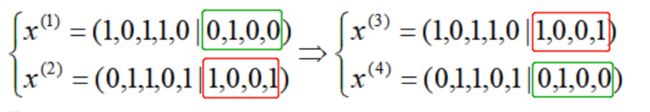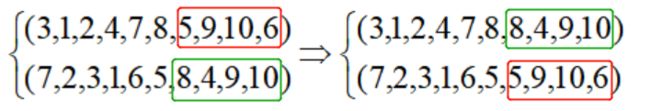离散优化的启发式迭代算法

本章介绍一些重要的、严格意义上真正的启发式算法。话不多说，进入正题。

1

构造型启发式算法

第一类启发式算法是构造型搜索（constructive search）算法。它通常从每一个自由决策变量的离散分量开始，在每次迭代中，在当前决策解固定情况下，一个先前自由的变量固定为一个可行值。在最简单的情况下，当没有自由变量存在时，搜索过程停止。

构造型搜索的主要难点在于如何选择下一个待固定的自由变量并且确定它的值,而贪婪（greedy）或短视（myopic）算法是解决这一问题最常见的方法。

贪婪构造型启发式算法每次迭代都会选择并固定下一个变量，这种方法在当前临时解的变量已经固定的情况下，可以保证下一个解的最大可行性，并且能够最大限度地改进目标函数值

换句话说，贪婪算法的规则是在目前已知内容的基础上，选择固定被选中概率最大的变量，从而得到更好的解。该算法在下一次选择时只能依靠局部信息，因此一般情况下存在风险，在贪婪算法中一个只有少数变量固定的并且看起来表现很好的解实际上会迫使搜索进入可行空间中非常差的区域，然后考虑到该算法的高效，有所损失在所难免。在极少数情况下，贪婪算法能得到精确的解（荒地能源案例展示过贪心算法）

案例传送门：网络流与图（四）

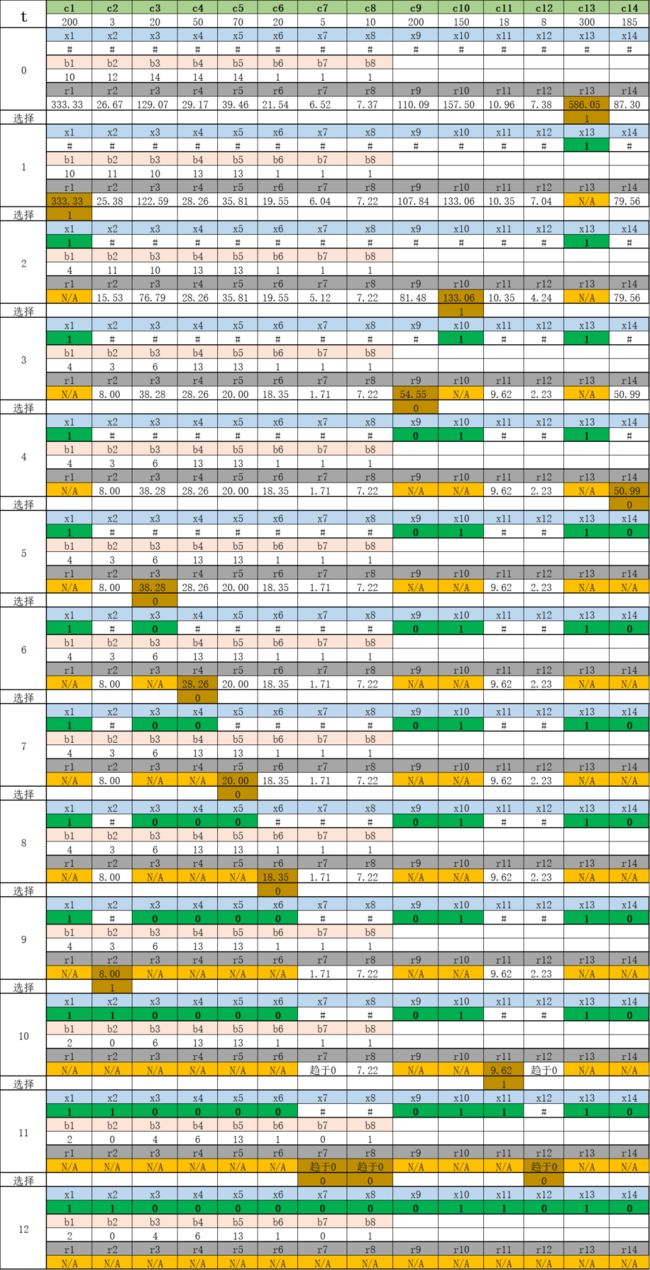
我们需要制定一个贪婪选择的准则——在选择任务时优先考虑具有高目标函数“价值”系数的任务，但同时需要考虑约束条件。通常情况下，以比率为衡量标准来权衡任务价值和客观约束条件，以NASA资本预算模型为例，可以构造比率：

分子考虑了两部分：选择任务的直接价值和它后续任务的潜在价值（依赖关系的可选择任务，随机分配一半价值）；分母把选定任务要消耗的剩余约束“资源”的分数相加。这个比率通过“性价比”，即价值与所使用资源的比值，实现目标和约束两方面的综合考量。

利用上述定义的比率，通过贪心算法得到NASA案例的搜索过程：

对于t=3，x9取值为0，因为若取1，将违反约束2；在t=6时刻，x4取0是因为与x3的依赖关系，也是因为约束关系；然后在t=9时刻，按照原理应取x11，但因为顺序关系，必须先取x2=1；最后是t=12时刻，根据约束可以一次性判断x7=x8=x12=0

最后得到的最优解值是671，可以比较由分支定界搜索得到的最优解值765。贪心算法是一种近似最优解，且会存在较大的风险。

所以只有在求解大规模，并且通常是非线性的高度组合的离散模型或者需要我们快速求解的情况下，才真正需要应用构造型搜索方法。

2

改进搜索启发式算法

运筹学专题开篇不久，我们介绍了搜索理论的基础，并展示了Dclub选址案例。该案例是在连续变量情况下进行的搜索算法(improving  search）

传送门：搜索理论基础

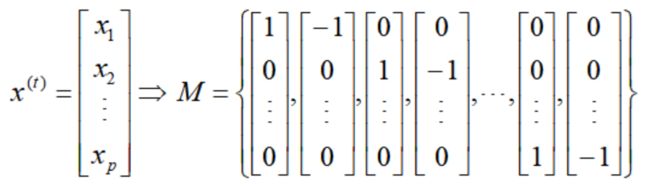
只要我们对该方法进行适当修改，就可以产生非常有效的启发式算法。对于离散形式的改进搜索，需要明确定义当前解的邻域。引入显式移动集合M来囊括所有可能的当前解的邻居解。

这里我们要注意如何选择移动集合M.一个穷尽的方法就是当前解所有分量都向前和向后移动一单位：

当然对于一些特殊的案例构造移动集合M也是不同的。我们以旅行商问题（TSP）的NCB电路板案例加以说明，但此之前首先我们要把TSP建立的模型改为二次分配模型（QAP）

案例传送门：离散优化模型

注释：离散优化模型一文对于NCB钻孔的距离表格抄错了，书中正确的距离是代码附录上D显示的部分，这里稍微注意一下

浏览路径是要访问的点的序列或排序，可以将TSP问题以QAP形式的决策变量将序列位置k分配给点i,引入决策变量：

比如在BCN案例中，一种路径可以表示为：

它表示以孔1为起点，每一次连接的下一个孔是什么。这里的路径是1-3-6-5-4-8-9-10-7-2，最后回到1

这样无论是对称不对称的TSP问题都可以被建模为一个整数非线性规划模型：

理解一下这里，若节点i与节点j相连，说明i的下一个序列位置是j，它们的y取值均为1，此时距离为dij,否则都为0.以上就是目标函数表达出来的意思。

回到NCB案例，应用离散改进搜索搜索，一个初始可行解显然为：

对应的总长度为d=3.6+3.6+7.1+7+9.9+25+10.3+10.2+3.6+26.4=106.7

对于NCB案例每次迭代的移动路径，是由不同序列位置置换得到的。比如初始序列是：1-2-3-4-5-6-7-8-9-10

假设下一次路径是1-2-5-4-3-6-7-8-9-10，那么就是交换了位置3和5.注意，不会出现相对于上一次，该次路径发生双重置换的情况，因为集合M的元素决定了每次移动的步数为一单位。也即：

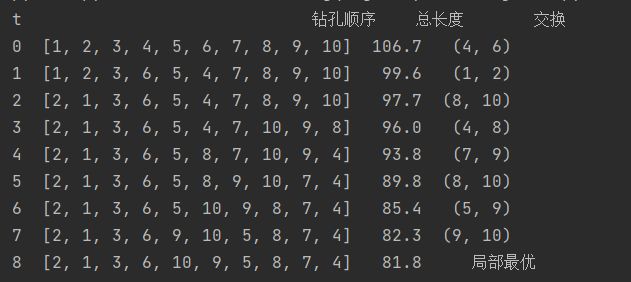
然后我们计算两两置换（45种组合）后目标函数值的变化量，取变化量最大的即可，下面展示了从初始解到局部最优解的过程（代码在附录上）：

上面得到的是全局最优解。但有些初始解搜索的局部最优解并非是全局最优解，比如下面尝试不同的初始解得到的局部最优：

对于大规模的场景，我们很难判断启发式最优解与局部最优解。因此尝试不同的初始值，重复上面的算法是一种改进算法：利用多起点（multistart）或保持从不同的起始解中获得的几个局部最优解进行启发式搜索，是一种改善改进搜索的启发式解的方法

3

禁忌搜索与模拟退火

上面介绍的两种启发式算法关注在局部最优解上。而元启发式算法（metaheuristic）借助一些高级策略，以期望获得更好的多元化搜索。我们介绍两种最经典的元启发式算法——禁忌搜索和模拟退火。

根据上面可知，一些得到局部最优解而停止迭代的原因是不存在改进方向了，如果我们继续考虑非改进方向有没有可能得到比局部最优解更优的解呢。根据数学知识，答案是肯定的。但这也会带来另外一个问题——可能会出现无限循环的情况。

非改进移动将导致改进搜索的无限循环，除非添加一些规定以防止重复的解

禁忌搜索（tabu search）就是一种方法：通过暂时禁止移动到近期出现过的解这种方式提高循环效率。但这种效果是防止短期循环，解在长时间的搜索过程中还是会发生重复。我们给出禁忌搜索的步骤：

禁忌算法存在一个禁忌列表，用来记录当前迭代中被禁忌的移动，并且每次迭代中只能选择非禁忌可行移动。在每次迭代操作后。任何立即返回到前一个点的移动都被添加到禁忌列表中。这样的移动在接下来几次迭代过程中是不被允许的，但最终所有移动都会从标签列表中删除，并再次可用。

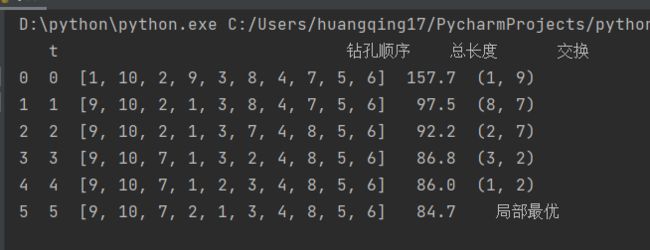
我们修改一下改进搜索代码，得到禁忌搜索的迭代结果：

最优解达到了全局最优解。

将非改进移动方向引入改进搜索的另一种方法是模拟退火（simulated annealing），因为其类似于为提高金属强度而对其缓慢冷却的退火过程。

模拟退火算法通过依概率接受非改进移动的方式来控制循环。这些概率由计算机随机生成

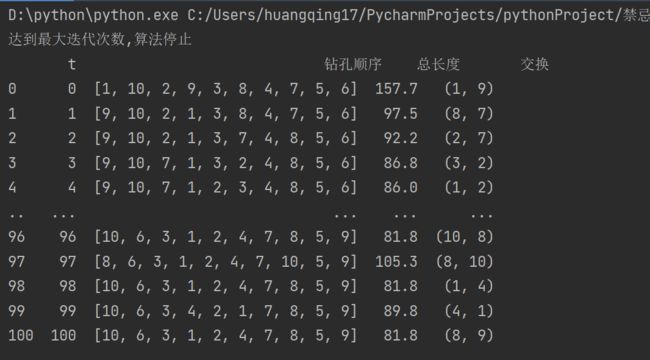
我们设置初始温度q=5,每次变化温度迭代次数为10，然后得到如下结果（部分）：

最后模型也得到了全局最优解。这就是模拟退火搜索的过程。

4

遗传算法

启发式算法通过模仿生物界自然选择的机制，利用时间不断改进群体的适应能力。进化元启发式算法（evolutionary metahearistics）扩大了启发式搜索的范围，这一算法超越任何单一解逐步进化的搜索范围。我们介绍其中最著名的一种——遗传算法（generic algorithms）

遗传算法通过组合群体中不同成员的解演化出更好的启发式优化解，用于组合群体解的标准遗传算法称为交配（crossover）

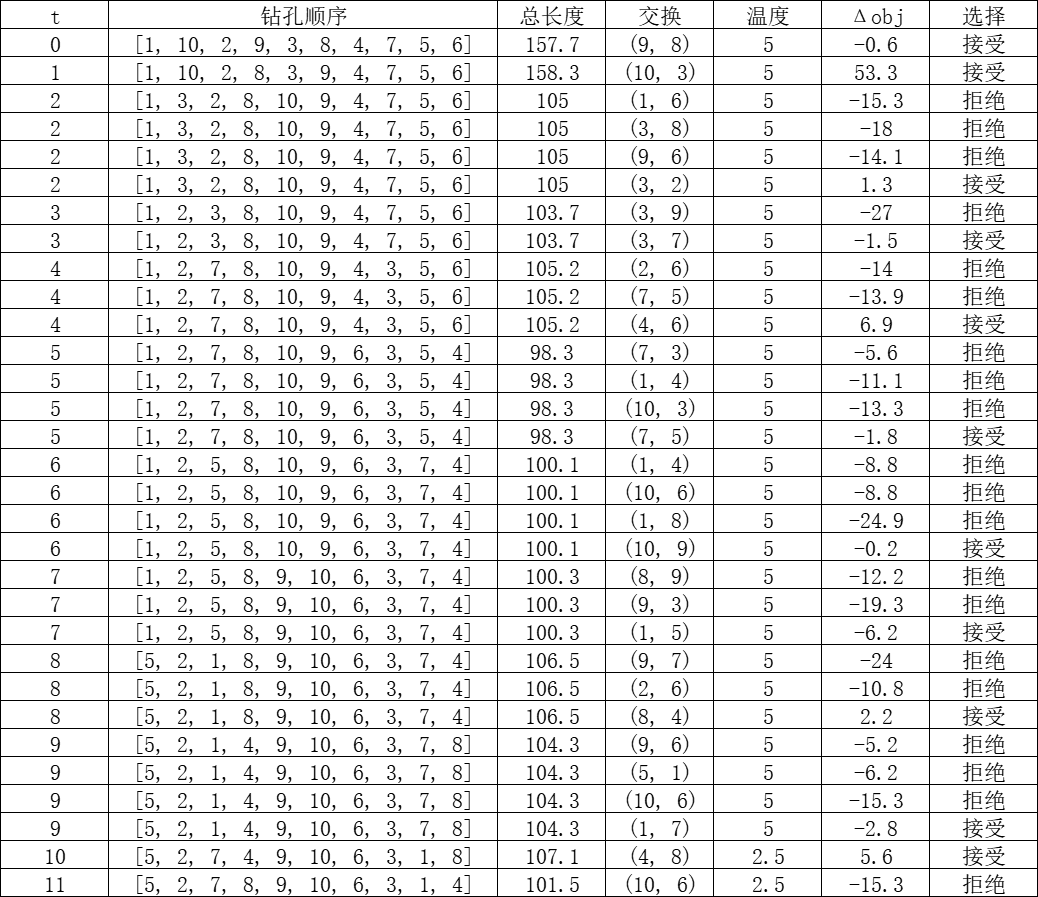
交配组合了一对“双亲”解，希望通过在同一点打破双亲向量并且通过将其中一个父代解的第一部分与另一个的第二部分重新组合的方式来产生一对“子代”解，反之亦然，也会产生相同的一对“子代”解

我们举一个例子来说明交配的过程，下面是一对解交配后得到另一对解：

就是把解的部分分量交换组合。

这种交配对于一些场景会产生一些问题，无法得到有用的解，比如NCB旅行商问题中，下面两个可行解（称为染色体）在基因（组成编码的元素称为基因）j=6处突变，产生的子代是：

这样的解显然不可行。因此有效的遗传算法搜索需要在编码问题的可行解中进行选择。我们可以通过一项被称为“随机密钥”的技术获得更好的编码。

原理就是生成一个规模与基因相同的随机数（0-1区间），然后依次由小到大对应基因编码的由小到大排序，比如：

由此，我们给出遗传算法搜索的一般步骤：

附录：

#NCB旅行商问题-改进搜索
import copy
import numpy as np
import pandas as pd


def get_change(Path,D):
    '''


    :param Path: 当前路径，列表形式
    :param D: 两两节点的距离numpy表
    :return:
    '''


    d_t = [D[i,Path[0]] if n == len(Path)-1 else D[i,Path[n+1]] for n,i in enumerate(Path)] #当前钻孔顺序的总长度


    di = {}
    for n, k in enumerate(Path):
        for g in Path[n+1:]:
            #交换序列k,g
            new_path = copy.deepcopy(Path)
            new_path[new_path.index(g)] = k
            new_path[n] = g
            d = [D[i,new_path[0]] if m == len(new_path)-1 else D[i,new_path[m+1]] for m,i in enumerate(new_path)]
            di[(k,g)] = round(sum(d_t) - sum(d),4)  #差值


    return di,sum(d_t)


if __name__ == '__main__':
    #钻孔之间的两两距离
    D = np.array([
        [0.000, 3.600, 5.100, 10.00, 15.30, 20.00, 16.00, 14.20, 23.00, 26.40],
        [3.600, 0.000, 3.600, 6.400, 12.10, 18.10, 13.20, 10.60, 19.70, 23.00],
        [5.100, 3.600, 0.000, 7.100, 10.60, 15.00, 15.80, 10.80, 18.40, 21.90],
        [10.00, 6.400, 7.100, 0.000, 7.000, 15.70, 10.00, 4.200, 13.90, 17.00],
        [15.30, 12.10, 10.60, 7.000, 0.000, 9.900, 15.30, 5.000, 7.800, 11.30],
        [20.00, 18.10, 15.00, 15.70, 9.900, 0.000, 25.00, 14.90, 12.00, 15.00],
        [16.00, 13.20, 15.80, 10.00, 15.30, 25.00, 0.000, 10.30, 19.20, 21.00],
        [14.20, 10.60, 10.80, 4.200, 5.000, 14.90, 10.30, 0.000, 10.20, 13.00],
        [23.00, 19.70, 18.40, 13.90, 7.800, 12.00, 19.20, 10.20, 0.000, 3.600],
        [26.40, 23.00, 21.90, 17.00, 11.30, 15.00, 21.00, 13.00, 3.600, 0.000],
            ])


    Li = []
    # path = [i for i in range(10)]
    path = [0,1,6,2,3,7,4,5,8,9]
    # path = [0,9,1,8,2,7,3,6,4,5]
    t = 0
    while True:
        di,distance = get_change(path,D)


        (k, g) = max(di, key=di.get)  # 找出变化量最大的置换位置
        if di[(k, g)] <= 0:
            Li.append([t, [i + 1 for i in path], distance, '局部最优'])
            break
        else:
            k_index, g_index = path.index(k), path.index(g)
            Li.append([t,[i+1 for i in path],distance,(k+1, g+1)])
            t += 1
            path[k_index] = g
            path[g_index] = k


    Re = pd.DataFrame(Li,columns=['t','钻孔顺序','总长度','交换'])
    print(Re)

#NCB旅行商问题-禁忌搜索
t, t_max = 0, 100  #初始化迭代次数与最大可迭代次数
taboo_li, taboo_times = {}, 6  #初始化禁忌列表以及禁止的次数
while True:
    if t > t_max:
        print('达到最大迭代次数,算法停止')
        break


    taboo_li = {s:t for s,t in taboo_li.items() if t < taboo_times}  #更新禁忌列表，满足次数的移动方向被移除
    di, distance = get_change(path, D)


    for (k,g) in list(di.keys()):
        #选择非禁忌的可行移动
        k_index, g_index = path.index(k), path.index(g)
        delta_x = '{}_{},{}_{},{}_{},{}_{}'.format(k_index, k, g_index, g, k_index, g, g_index, k)  # 记录移动方向
        if delta_x in list(taboo_li.keys()):
            di.pop((k,g))


    if len(di) == 0:
        print('不能通过移动集合M的非禁忌方向得到可行邻居解,算法停止')
        break
    else:
        if max(di.values()) > 0:
            (k, g) = max(di, key=di.get)  # 找出变化量最大的置换位置
        else:
            (k,g) = random.choice(list(di.keys()))
        k_index, g_index = path.index(k), path.index(g)
        Li.append([t, [i + 1 for i in path], distance, (k + 1, g + 1)])
        taboo_li = {s:t+1 for s,t in taboo_li.items()}  #循环一次，禁止次数+1


        delta_x = '{}_{},{}_{},{}_{},{}_{}'.format(k_index, k, g_index, g, k_index, g, g_index, k)  # 记录移动方向
        taboo_li[delta_x] = 0      #记录delta_y,{1_1,1_9,4_9,4_1}:1


    t += 1
    path[k_index] = g
    path[g_index] = k


Re = pd.DataFrame(Li,columns=['t', '钻孔顺序', '总长度', '交换'])

#NCB旅行商问题-模拟退火 
Li = []  #记录每次迭代的信息
# path = [i for i in range(10)]
# path = [0, 1, 6, 2, 3, 7, 4, 5, 8, 9]
path = [0, 9, 1, 8, 2, 7, 3, 6, 4, 5]


t, t_max, q = 0, 50, 5  #初始化迭代次数\最大可迭代次数\起始温度


while True:
    if t > t_max:
        print('达到最大迭代次数,算法停止')
        break


    di, distance = get_change(path, D)
    while True:
        (k,g) = random.choice(list(di.keys()))
        delta_obj = di[(k,g)]               #净目标函数改进值
        accept_p = math.exp(delta_obj / q)  # 接受概率
        if delta_obj > 0 or accept_p >= random.random():
            k_index, g_index = path.index(k), path.index(g)
            Li.append([t, [i + 1 for i in path], distance, (k + 1, g + 1), q, delta_obj, '接受'])
            break
        else:
            k_index, g_index = path.index(k), path.index(g)
            Li.append([t, [i + 1 for i in path], distance, (k + 1, g + 1), q, delta_obj, '拒绝'])
            continue


    t += 1
    path[k_index] = g
    path[g_index] = k
    if t % 10 == 0:
        q = q/2




Re = pd.DataFrame(Li,columns=['t', '钻孔顺序', '总长度', '交换', '温度', 'Δobj', '选择'])
Re.to_csv(r'模拟退火.csv',index=False)