机器学习——朴素贝叶斯（手动代码实现）

朴素的我，决定朴素地徒手实现贝叶斯算法！
摒弃sklearn 这个体贴善解人意把一切都打包封装好的妈妈
再见了sklearn 妈妈
我要自己手动实现
哪怕前方困难重重
哪怕我此刻还在发牢骚
但我还是要说，撒哟娜拉sklearn妈

看了知乎阿婆主的分析，我想，我对朴素贝叶斯的理解应该已经有了质的飞跃！！！

首先，我混淆了很久的先验概率和后验概率之分！！！

先验概率，就是基于统计、经验等得到的概率，为后续计算所用。
一个概率是先验还是后验，是不一定。

1. 朴素贝叶斯的朴素理解

朴素贝叶斯的分类本质，就像是光看我的身体特征，分析我是男的概率有多大，是女的概率有多大。

朴素贝叶斯其实是我们潜意识里常用的分类方法，很不科学，但大概率会是正确的。

例如走在大马路上，迎面走来一个人，平胸、有喉结、短头发、眉毛粗、肢体粗犷

根据这个人的特征，如果是阅人无数的我，应该会下意识认为这是个男生【朴素贝叶斯在作祟】

因为在我认识的那一堆人中，有这样特征的虽然男男女女都有，但是在这样的特征中，男性的占比其实是比女性要大很多。

以上就是朴素贝叶斯的分类思想，主要应用的是归纳法。

目标：有个对象，它的特征为$\hat{X}=\{x_0,x_1,....x_m\}$，现需要判断这个对象究竟是属于哪个类别
判断方式：在历史数据中找到符合这个特征的所有对象，计算在这些对象中，各类别的占比。

• 哪个类别的占比大，就判定这个对象是哪个类别

当然，朴素贝叶斯是有可能分类错误的！！！刻板印象不可有，但如果没有办法，刻板印象在一定程度上，就是经验
一个人的经验丰富，可能指的就是，这个人的朴素贝叶斯分类正确率较大，能够在面对某些情况时，根据他个人的经验（朴素贝叶斯），来做出正确概率较大的判断！！！

2. 举例理解朴素贝叶斯公式

首先，朴素贝叶斯能够通过计算，分类正确率较大的前提是，各特征之间没有相关性。

举个：现有关于人体特征与性别的历史数据，其中特征为3种（即特征）
$x_1（平胸与否：平胸、不平胸）、x_1（是否有喉结：有喉结、无喉结）、x_2（头发长度：短、中、长）$，
性别 $y$ 为 2 种：男、女

目标：现在有个人的身体特征为 $x_0=不平胸、x_1=有喉结、x_2=中头发$，请判断这人是男or女 ？

目前有两种根据概率来进行判断的思维：非常容易混淆！！！！！

判断思维1：计算出这个人的身体特征，在历史数据中符合这个身体特征的所有对象里，性别为男的概率有多大，性别为女的概率又有多大。
即：

• 符合身体特征的所有对象中，男性的占比是多少$P（男|\hat{X}）$
• 符合身体特征的所有对象中，女性的占比是多少$P（女|\hat{X}）$

方式1：联合筛选，计算概率【正常人的思维漏洞】

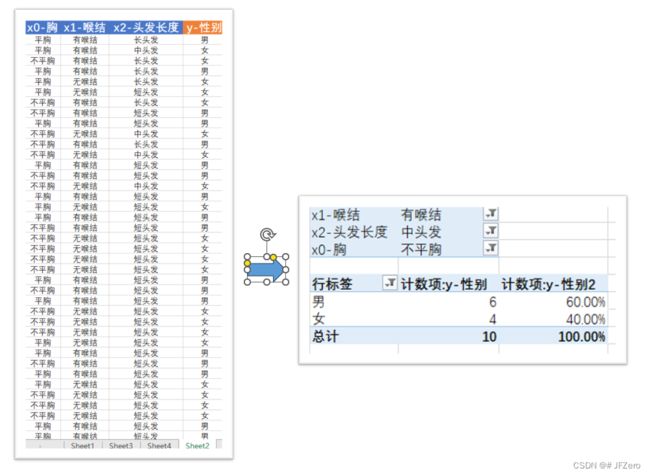
如果是用Excel操作，那就很简单了，直接挨个挨个筛选：先筛选不平胸、再筛选有喉结的、再筛选中头发的。

这三个条件同时满足的共有10个人，其中，男性占60%，女性占40%

可以看出，男生比例60%比较大，所以可以判断为这个$x_0=不平胸、x_1=有喉结、x_2=中头发$的人为男生。

乍一听，很合理，我都懵了，这样的判断方式，没毛病呀！！！

但这样的思维，有个非常大的缺陷问题！！！！！！有漏洞！！！

漏洞就是，万一其中某个特征的对象，本来就很少呢？

例如，假设在头发特征100个人里，中头发的人如果只有10个，并且如果中头发与性别关系不大：这种情况下，对中头发的筛选，会同时筛除掉包含另外两个特征（胸和喉结）的（短、长头发）人群。

简单来说，就是如果某个特征与分类结果关系不大，且该特征占比差异悬殊，那么对该特征的筛选，有可能会影响到其他特征的数据，最终又可能导致分类结果出错。

再打个比方：身高与智商无关，但在历史数据中包含有身高、基因、记忆力等特征数据X，以及对应的智商Y（高中低）。

当有个人，身高2.2米，基因xx，记忆力xx，现在要判断他智商Y的类别。

当我们筛选身高2.2米时，可能直接把99.999%的人全部筛出去了，最终可能只剩下2个人，那这2个人的智商为高、中、低的概率，还能够作为判断那个人智商的依据吗？

显然不能，因此：当特征与类别的关系不大时，筛选特征，有可能会错误地影响分类结果

方式2：条件独立，计算概率【改进方式1】

那么，第一种思维的计算方式有漏洞，我们要对第1种思维的计算方式，进行改进。

改进的方向：避免特征筛选对其他特征的影响

当各个特征之间，是相互独立，即不相关的情况下才能应用此改进的计算方式。
这句话本身是有问题的，且先暂时这么想

也就是各特征是直接与类别有关，例如假设一个人的类别是胖、瘦，那么身高特征、外貌特征可以直接影响到类别，但身高与外貌的取值无关。一个人既高又美的概率 P = P高*P美——身高与外貌相互独立

第2种改进思维：计算出各类别中，这种身体特征出现的概率有多大，即

• 男性中出现不平胸、有喉结、中长发的概率$P（\hat{X}|男）$
• 女性中出现不平胸、有喉结、中长发的概率$P（\hat{X}|女）$

完全跟第一种思维反过来了！！！！

但千万不能再用刚才的表格筛选：筛选出男性，再计算既不平胸、又有喉结、且还是中长发的人数占比；筛选出女性，再计算既不平胸、又有喉结、且还是中长发的人数占比！！不！不能这样，这样用联立的条件（同时成立的条件），还是会让中长发的影响到其他特征的数据

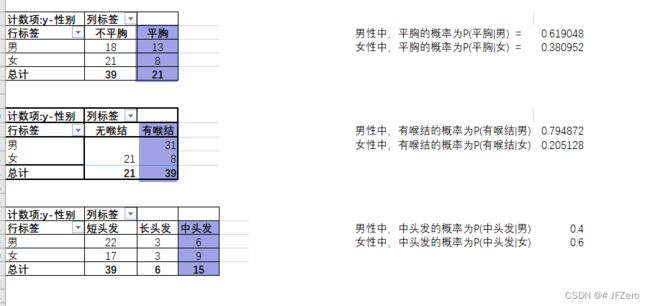
这些特征都相互独立的情况下，应分别计算出男性的各个特征占比：

• 男性中，不平胸的人数占比为 $P（不平胸|男）$
• 男性中，有喉结的人数占比为 $P（有喉结|男）$
• 男性中，中头发的人数占比为 $P（中头发|男）$

这些特征是相互独立的，也就意味着，在男性中同时出现不平胸、有喉结、中长发的概率为
$P（\hat{X}|男）=P（不平胸|男）\ast P（有喉结|男）\ast P（中头发|男）$

• 女性中，不平胸的人数占比为 $P（不平胸|女）$
• 女性中，有喉结的人数占比为 $P（有喉结|女）$
• 女性中，中头发的人数占比为 $P（中头发|女）$

这些特征是相互独立的，也就意味着，在女性中同时出现不平胸、有喉结、中长发的概率为
$P（\hat{X}|女）=P（不平胸|女）\ast P（有喉结|女）\ast P（中头发|女）$

这样的计算，虽然避免了一个特征的筛选，影响其他特征数据的情况，但还是对分类概率本身有很大影响。

因为，如果某些特征本来占比就少，例如假设中头发的人数本来就很少很少，那么无论男性、还是女性中，$P（中头发|男）$和$P（中头发|男）$都会非常小

这就像是，全中国身高超过2.2米的人数占比为0.1%，非常小。。。。而男性中，身高超过2.2米的占比也非常小，可能为0.11%
那么如果用男性中的身高占比，去计算分类概率时，会非常拉低分类概率的。

即，计算出来的$P（\hat{X}|男）$和$P（\hat{X}|女）$也会很小。

所以，为了避免各个特征自身占比的影响，就让各类别中的每个特征占比，都分别去除以各特征自身的占比。

这就好像是，全中国身高超过2.2米的占比为0.1%，本身就很小，那我用0.11%除以0.1%，不久可以去除特征自身占比偏小的影响了嘛！

但相除的实际数学意义是什么呢？拿$\frac{P（中头发|男）}{P（中头发）}$作为例子，

$P（中头发|男）=\frac{男性中的中头发人数}{男性总人数}$

$P（中头发）=\frac{(总人数中的中头发数)}{总人数}$

则 $\frac{P（中头发|男）}{P（中头发）}=\frac{男性中的中头发人数}{男性总人数}➗\frac{总人数中的中头发数}{总人数}=\frac{男性中的中头发数}{总人数中的中头发数}✖\frac{总人数}{男性总人数}$

亮点来了！！！！！！

这里，其实就等于中头发中，性别为男的概率 $P（男|中头发）$
譬如，50个男里有10个中头发，总共100个人里有30个中头发——那不就相当于100个人里，总共有30个中头发，其中男的占了10个

所以， $P（男|中头发）=\frac{P（中头发|男）}{P（中头发）}\ast P（男）$

$=\frac{男性中的中头发数}{总人数中的中头发数}✖\frac{总人数}{男性总人数}\ast \frac{男性总人数}{总人数}=\frac{男性中的中头发数}{总人数中的中头发数}$

那么$P（男|中头发）=\frac{P（中头发|男）}{P（中头发）}\ast P（男）$ ，这就是贝叶斯公式的计算过程呀！！！！

我觉得我悟了呜呜呜呜,虽然感觉任何正常人看了，都会不知所云。。。但我真的悟了。。。。还是要写下来，才能梳理清自己的思维
手动实现算法的代码，其实是一件比理解更容易的事，能理解一件事，对我而言，真的不容易
因为脑子，有时候是骗人的，你以为的你以为，有时真的只是你以为

但即便是我理解了，我也无法真的能用逻辑清晰，简洁易懂的话，让别人理解。。。

更完整的概率计算如下，
$P（男|不平胸）=\frac{P（不平胸|男）}{P（不平胸）}\ast P（男）$

$P（男|有喉结）=\frac{P（有喉结|男）}{P（有喉结）}\ast P（男）$

$P（男|中头发）=\frac{P（中头发|男）}{P（中头发）}\ast P（男）$

$P（男|不平胸\&有喉结\&中头发）=\frac{P（不平胸\&有喉结\&中头发|男）}{P（不平胸\&有喉结\&中头发）}\ast P(男)$

=$\frac{P（不平胸|男）\ast P（中头发|男）\ast P（有喉结|男）}{P（不平胸）P（有喉结）P（中头发）}\ast P（男）$

无知的困惑1

之前有个困惑，既然各个特征之间是相互独立的，那为什么不用下边这种方式来计算？
$P（男|不平胸\&有喉结\&中头发）=P（男|不平胸）P（男|有喉结）P（男|中头发）$

$P（男|不平胸\&有喉结\&中头发）$表示：在既不平胸、又有喉结、同时还留中头发的对象里，男性的占比为多少= $\frac{不平胸、有喉结、中头发的男性人数}{不平胸、有喉结、中头发总人数}$

P（男|不平胸）表示：不平胸的对象里，男性占比为多少 = $\frac{不平胸的男性人数}{不平胸总人数}$
P（男|有喉结）表示：有喉结的对象里，男性占比为多少 = $\frac{有喉结的男性人数}{不平胸总人数}$
P（男|中头发）表示：中头发的对象里，男性占比为多少 = $\frac{中头发的男性人数}{中头发总人数}$

$\frac{不平胸的男性人数}{不平胸总人数}\ast \frac{不平胸的男性人数}{不平胸总人数}\ast \frac{中头发的男性人数}{不平胸总人数}\ne \frac{不平胸、有喉结、中头发的男性人数}{不平胸、有喉结、中头发总人数}$

因此，$P（男|不平胸\&有喉结\&中头发）\ne P（男|不平胸）P（男|有喉结）P（男|中头发）$

$P（男|不平胸\&有喉结\&中头发）$中，【不平胸&有喉结&中头发】是一个既定统计事实，不能是通过特征独立后的概率相乘计算得到

无知的困惑2

另外，还有个地方是我困惑的：在课本里的朴素贝叶斯分母部分，是用的全概率公式
$P（男|不平胸\&有喉结\&中头发）=\frac{P（不平胸\&有喉结\&中头发|男）}{P（不平胸\&有喉结\&中头发）}\ast P(男)$的分母部分：

为什么是：$P（不平胸\&有喉结\&中头发）=P(不平胸\&有喉结\&中头发|男)P(男)+P（不平胸\&有喉结\&中头发|女）P（女）$

为什么不是:$P（不平胸\&有喉结\&中头发）=P(不平胸）P（有喉结）P(中头发）$

独立的新知识：条件独立和独立，是不一样的！！！我之前的说法又错了！！！

条件独立：在结果是既定发生的条件下，特征对结果的影响是独立的，即$P(A、B|条件1）=P(A|条件1)\ast P(B|条件1)$
但是：$P(A、B）不一定等于P(A)\ast P(B)$

A，B在条件1发生下相互独立等价于A在条件1下是否发生和B是否发生无关。【盗取别人的说法】

条件独立就好像是，唐僧取经成功的情况下（既定条件），孙悟空的打怪个数和猪八戒的摆烂次数，是相互独立的。
好像不贴切哈，再换一个：考试满分的情况下（既定条件），妈妈送饭和熬夜学习这两个特征，是相互独立的。

算了。。。好像都不怎么贴切，但就是这么个意思，要有个条件前提下，特征相互独立的情况。

独立：特征之间是相互独立的。【条件影响无作用】
也就是$P(A、B）=P(A)\ast P(B)$
由于条件影响无作用，因此，
P(A|条件1) = P(A)、P(B|条件1)=P(B)
P(AB|条件1) = P(AB)=P(A)*P(B)

条件独立和独立之间，并没有包含关系。

即，两个特征的条件独立，并不能说明这两个特征独立。

• 例如，当处在一个总体学习成绩特别好的班级里，家境和教育环境对成绩的影响，是相互独立的。
• 即，在一个总体学习成绩特别好的班级，家境虽然有些不同，但教育环境其实是相近的，因此家境与教育环境之间，相对而言是独立的。
• 但如果没有这个班级的前提，也就是如果单纯考量家境和教育环境的关系，通常会发现家境其实是会对教育环境有较大的影响，有较强的相关性：家境好的家庭，通产会将孩子送到教育环境好的地方学习

另外，两个特征独立，并不能说明这两个特征基于某个条件也独立。

• 例如，在无特定的场景条件下，尿布和啤酒的销量，是相互独立的。即尿布卖多卖少，与啤酒无关
• 但如果是在已婚妇女的超市购物场景条件下，统计可发现尿布和啤酒的销量之间是有相关性的，尿布销量高，啤酒销量也高
• 原因：已婚妇女有孩子，有丈夫，一次性购物通常会同时买。

我也不知道举例是否正确

朴素贝叶斯是基于条件独立的前提下进行的，而不是独立

那么$P（不平胸\&有喉结\&中头发）=$

$P(不平胸\&有喉结\&中头发|男)P(男)+P（不平胸\&有喉结\&中头发|女）P（女）=$

$P(不平胸|男)\ast P(有喉结发|男)\ast P(中头发|男)\ast P(男)+P(不平胸|女)\ast P(有喉结|女)\ast P(中头发|女)\ast P(女)$

感动…朴素贝叶斯的理论部分，差不多完结了，好像还有拉普拉斯平滑。。。这个就很简单了，先不搞

2.1 朴素的朴素贝叶斯公式

总公式：
$P（男|不平胸\&有喉结\&中头发）=\frac{P（不平胸\&有喉结\&中头发|男）}{P（不平胸\&有喉结\&中头发）}\ast P(男)$

$P（女|不平胸\&有喉结\&中头发）=\frac{P（不平胸\&有喉结\&中头发|女）}{P（不平胸\&有喉结\&中头发）}\ast P(女)$

比较$P（男|不平胸\&有喉结\&中头发）和P（女|不平胸\&有喉结\&中头发）$的值，哪个大就判定为哪种类别（男、女）

细节公式-分子部分：
P（不平胸&有喉结&中头发|男）= P(不平胸|男) *P(中头发|男)*P(有喉结|男)

细节公式-分母部分：
P（不平胸&有喉结&中头发）
= P(不平胸&有喉结&中头发|男)P(男)+P(不平胸&有喉结&中头发|女)P(女)
= P(不平胸|男)*P(有喉结|男)*P(中头发|男)*P(男)+P(不平胸|女)*P(有喉结|女)*P(中头发|女)*P(女)

更细节公式-单个概率部分：
分子和分母的计算，都是单个特征的条件概率计算，例如P(有喉结|女)
具化到统计时，如下

$P(有喉结|女)=\frac{女性中有喉结的人数}{女性人数}$

$P(男)=\frac{男性人数}{总人数}$

不行！！没有拉普拉斯平滑，我的第一个朴素贝叶斯代码就遇到大问题了

2.1.2 拉普拉斯平滑

如果：出现数据里没有的某个特征值，那么条件概率计算就会为0，则无法进行分类。

例如，如果我们要预测对象，ta的特征是，不平胸、无头发、有喉结，注意，无头发这个特征在原来的数据里是没有的，那么 P（无头发|女）,或 P（无头发|男），都为0

那么根据朴素贝叶斯公式，分母部分就会为 0 ，导致无法进行计算和分类 ：
P（不平胸&有喉结&中头发）= P(不平胸|男)*P(有喉结|男)*P(无头发|男)*P(男)+P(不平胸|女)*P(有喉结|女)*P(无头发|女)*P(女)

无法计算出概率，这就无法进行分类了呀！！！我们希望的情况是：即使出现新的特征，也能根据其他原有的特征进行分类

也就是，即使无头发这个特征值没有，但我们还可以根据不平胸、有喉结这两个特征进行分类啊

这就好像，如果你人生中第一次看到光头，你也可以根据喉结来判断这个光头是男是女。

因此，要解决这个问题，需要引入平滑算法，让它在某个问题上能够圆滑地糊弄过去，而且糊弄的不会太糟糕。

可见圆滑的糊弄，并不是人情世故里独有的招数，在数学的世界里，那也是非常好用的！

拉普拉斯平滑呢，就是给每个特征的条件概率计算，引入拉普拉斯算子。

这个算子呢，其实就是给每个特征的条件概率计算，分子部分+λ，分母部分+S*λ

• λ，一般是1
• S，表示该特征的值个数，例如头发特征有3种，短头发、中头发、长头发，那么S就是3

所以，P（无头发|女） = $\frac{女性中无头发的人数+\lambda }{女性人数+S\ast \lambda }=\frac{女性中无头发的人数+1}{女性人数+3\ast 1}$

即使女性中无头发的人数=0,P（无头发|女）也不再是0，而是$\frac{0+1}{女性人数+3\ast 1}$

P（无头发|男）也是如此

至此，朴素贝叶斯，暂时告一段落

但这就结束了吗！！！！！啊！！！！并没有！！！！！！

要知道，前边所讲的朴素贝叶斯分类，都是基于特征是有界的离散值来进行的分类。

例如，有喉结、无喉结，就两种特种值。

但有些特征值，是连续的：例如，金钱、年龄、点击率、销售额等等

这种连续的特征值，该怎么计算出条件概率呢？——以后再说！先把最简单的用代码实现一下

2.1.3 朴素贝叶斯 — 手动代码

收回我当初无知的言论...写代码也很难...哭了
难就难在如何设计数据结构，思路很简单

• 1. 先统计各类型下各个特征值的对象数——存入字典【小复杂】
• 2. 计算并预测每个对象的类型
  • ① 针对单个对象的特征数据，索引获取字典中的对象数
  • ② 根据朴素贝叶斯公式，计算各类型的概率【增加拉普拉斯算子】
  • ③ 以概率最大的类型为预测结果，返回该类型

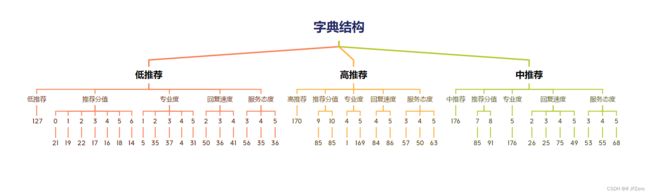
字典设计如下，叶子节点全是统计的对象数：
如果要获取字典中，低推荐类型中，专业度为5的对象数，
则字典索引为：字典结构[ 低推荐 ][ 专业度 ][ 5 ]

import numpy as np
import pandas as pd

# 获取所需数据：'推荐分值', '专业度','回复速度','服务态度','推荐类型'
datas = pd.read_excel('./datas4.xlsx')
important_features = ['推荐分值', '专业度','回复速度','服务态度','推荐类型']

datas_1 = datas[important_features]
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)
X_features = X.columns
Y_features = important_features[4]
rows,columns = datas_1.shape

# 1. 计算各个统计概率：P(推荐分值|各推荐类型)P(专业度|各推荐类型)P(回复速度|各推荐类型)P(回复速度|各推荐类型)P(各推荐类型)
# 如何获取具体有哪些特征、有哪些类别？——集合set函数
# 如何计算各个统计概率？——python自带的count函数
# 如何保存各个统计概率？——字典，将set里的值作为键，将count

# 集合获取特征、类别里的值
datas_dict = {}
for i in important_features:
    words = set(datas_1[i])
    datas_dict[i] = set(datas_1[i])

# 统计各特征、类别的数据，存入字典：字典结构是需要好好设计的！！！
groups = datas_1.groupby(Y_features) # 按类型分组，每组分别是一个类型的数据
datas_count = {}
for i in datas_dict[Y_features]:  # 依次获取各类型的值
    dict_temp = {}
    group = groups.get_group(i) 
    num1 = group.shape[0] # 获取当前类型组的对象数（即有几行数据）
    dict_temp[i] = num1
    """依次统计当前类型下，各个特征中-每种特征值的对象数"""
    for a in X_features: # 依次获取各个特征
        dict_Xtemp = {}
        group1 = group.groupby(a) # 按当前特征分组，每组分别是当前类型-当前特征下的数据
        for b in datas_dict[a]: # 依次获取当前特征的特征值
            try:
            	"""获取当前类型-当前特征-当前特征值组的对象数（即有几行数据）
            	（如果没有该特征值，程序会报错，因此捕获错误后让程序继续统计）"""
                num2 = group1.get_group(b).shape[0]
                dict_Xtemp[b] = num2
            except:
                pass
        dict_temp[a] = dict_Xtemp

    datas_count[i] = dict_temp
    print(datas_count)

# 基于朴素贝叶斯公式，计算单个对象的各类别概率，以概率最大的类别为预测类别，输出预测的类别
def predict(X):  # 只对每一行的X值进行计算，即预测每个对象的类别
    P_Y = []
    labels = list(datas_count.keys())
    for i in labels:  # 推荐类型
        P = 1
        P_i = datas_count[i][i]/len(Y) # P(当前类型)
        for j in X.index: # 所有特征
            """ 如果原数据中某个类型下没有某个特征值，则该类型下就没有X[j]这个键，
            那么获取datas_count[i][j][X[j]]键值时程序会报错：
            因此，需要捕获报错，在except中，将datas_count[i][j][X[j]]设置为0，再另行计算
            （也就是当找不到某个特征值，就赋值为0，而不是让程序报错）
            """
            try:
                P_up = datas_count[i][j][X[j]]+1  # +1是拉普拉斯平滑算子
                # len(datas_count[i][j])是拉普拉斯平滑算子，表示该特征的特征值个数
                P_down = datas_count[i][i]+len(datas_count[i][j]) 
                P *= (P_up/P_down)
                print(f"【{j}】值为{X[j]}，{i}人数为{datas_count[i][j][X[j]]}:",P_up,P_down,f"占比{round(P_up/P_down*100,2)}%")

            except:
                P_up = 0 + 1
                P_down = datas_count[i][i]+len(datas_count[i][j])
                P *= (P_up/P_down)
                print(f"【{j}】值为{X[j]}，{i}人数为0:", P_up,P_down,f"占比{round(P_up/P_down*100,2)}%")
       	"""记得要 P(特征|当前类型)*P(当前类型)，
        只计算了分子部分，不计算分母部分，因为分母部分值相同"""
        P_Y.append(round(P*P_i,8)) 
    # 获取概率最大的类别名称
    Y_hat = labels[P_Y.index(max(P_Y))]
    return Y_hat

# 应用了pandas中的apply函数，将每行数据都进行predict运算预测
Y_hat = X.apply(predict,axis = 1)

print(f"分类准确率：{sum(Y==Y_hat)/len(Y)*100}%")

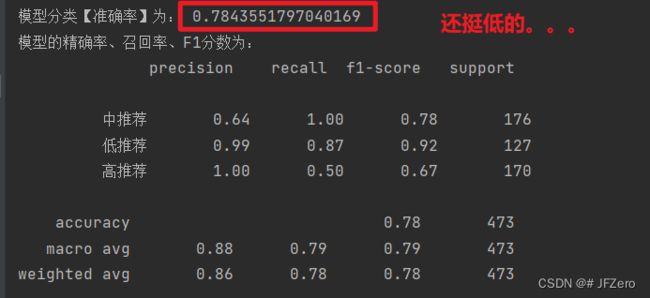
最终分类结果如下

但其实，朴素贝叶斯分类没那么准确的，之所以这次分类准确的原因，是因为原数据中的推荐类型是严格按照推荐分值进行划分的
高推荐：推荐分值≥9
中推荐：8≥推荐分值≥7
低推荐：6≥推荐分值≥0

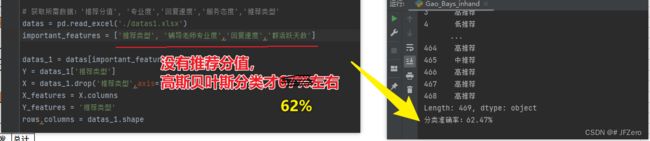
假设这次，不用推荐分值参与分类计算了，来看看朴素贝叶斯分类的情况

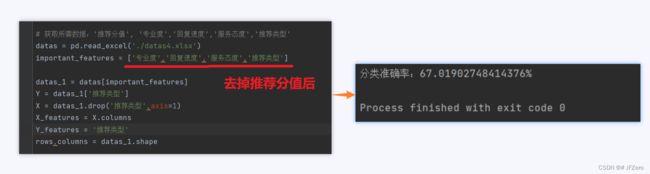
惨不忍睹，不忍直视…这是朴素贝叶斯的普遍情况，分类速度很快，但是准确率是堪忧的！
无所谓辣，人各有所长，有所短，哪能都这么完美

3. 朴素-高斯贝叶斯

3.1 基础理解

上述的朴素贝叶斯，都是基于特征值是有限的离散值，

• 如头发这个特征，有三个特征值：短头发、中头发、长头发
• 如喉结这个特征，有两个特征值：有喉结、无喉结

可是有些特征是连续的，比如说销售额、利润、身高、年龄、存款
身高：165cm、166cm、188cm等等连续

【不知道为什么，最近思考数据，第一时间涌现上来的，都是钱。。。。】

当这些连续的特征值，也会影响分类时，我们同样需要纳入考量。

可是，连续的特征值，很难进行对象数的统计呀…
总不能每个身高，都分别统计对应的人数吧，比如男性中，身高为166cm的有多少人

那就要很多很多很多很多的统计了，从1cm到250cm，依次进行统计
虽然这种苦力活是交给电脑，但是我自己等它干那苦力活，等得也是很烦躁的

因此，有人说，可以给这种连续的特征值，进行阶段性的划分，比如

• 低于155cm：矮
• 低于170cm：略矮
• 低于180cm：高
• 高于180cm：非常高

这样的划分呢，很麻烦…而且万一人为划分的有问题，那就不好辣

那么就可以引进【朴素-高斯贝叶斯】

朴素-高斯贝叶斯的前提是，特征值是服从正态分布的，然后通过正态分布的概率密度函数，计算出对应的P值。

哇，忽然发觉，之前学假设检验时的统计学基础，还是派上用场了…
果然，数学知识是相通的，数学，真的是…太神奇了
哎…

但是要注意，这里的P值，并非假设检验中的P值。

假设检验中的P值，其实求的是概率密度函数的积分（面积）
$P={\int }_{下限}^{上限}\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}dx$
但是，朴素-高斯贝叶斯里的P值，求得是概率密度函数的值（高度）
$P=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$

其中，朴素高斯贝叶斯公式里的具体参数解释
$P(特征值|类别)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$

• x：表示当前对象的具体特征值
• μ：表示当前类型下的当前特征均值
• σ：表示当前类型下的当前特征的标准差

其实很简单，就是在原来的代码里，对指定的特征的概率计算，换成正态分布的概率密度公式计算就好。

但是。。。我实在是懒得了

3.2 高斯贝叶斯 - sklearn代码

sklearn中的高斯贝叶斯，不知道是不是将所有离散值，也用概率密度函数来计算概率值

from sklearn import naive_bayes
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import classification_report

# 获取所需数据：'推荐分值', '专业度','回复速度','用户群活跃天数'
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐类型','推荐分值', '专业度','回复速度','用户群活跃天数']
datas_1 = datas[important_features]

# 明确实值Y为'推荐分值'，X分别为'专业度','回复速度','用户群活跃天数'
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)

# 1. 建立模型
classifier = naive_bayes.GaussianNB()
classifier.fit(X,Y)

# 2. 学习模型
classifier.fit(X,Y)
Y_predict = classifier.predict(X)
result_P = classifier.predict_proba(X)


# 3. 衡量模型
accurency = classifier.score(X,Y)
PRF = classification_report(Y,Y_predict)


# 输出模型最优状态下的参数及衡量模型的指标

print("模型分类【准确率】为：",accurency)
print("模型的精确率、召回率、F1分数为：")
print(PRF)

print('【模型分类，实际分类】的对比如下：')
for index,value in enumerate(zip(Y_predict,Y)):
    print(value)
    print(result_P[index])
# print(result_P)

手动演算一下sklearn的高斯贝叶斯计算过程

3.3 高斯贝叶斯 - 手动代码

import math

import numpy as np
import pandas as pd

# 获取所需数据：'推荐分值', '专业度','回复速度','服务态度','推荐类型'
datas = pd.read_excel('./datas1.xlsx')
important_features = ['推荐类型','推荐分值', '专业度','回复速度','用户群活跃天数']

datas_1 = datas[important_features]
Y = datas_1['推荐类型']
X = datas_1.drop('推荐类型',axis=1)
X_features = X.columns
Y_features = '推荐类型'
rows,columns = datas_1.shape

# 1. 计算各个统计概率：P(推荐分值|各推荐类型)P(专业度|各推荐类型)P(回复速度|各推荐类型)P(回复速度|各推荐类型)P(各推荐类型)
# 如何获取具体有哪些特征、有哪些类别？——集合set函数
# 如何计算各个统计概率？——python自带的count函数
# 如何保存各个统计概率？——字典，将set里的值作为键，将count



# 集合获取特征、类别里的值
datas_dict = {}
for i in important_features:
    words = set(datas_1[i])
    datas_dict[i] = set(datas_1[i])

# 统计各特征、类别的数据，存入字典：字典结构是需要好好设计的！！！
groups = datas_1.groupby(Y_features)
datas_count = {}
for i in datas_dict[Y_features]:
    dict_temp = {}
    group = groups.get_group(i)
    num1 = group.shape[0]
    dict_temp[i] = num1/len(Y)
    for a in X_features:
        dict_Xtemp = {}
        mean = group[a].mean()
        σ = group[a].std()
        dict_Xtemp = (mean,σ)
        dict_temp[a] = dict_Xtemp

    datas_count[i] = dict_temp
print(datas_count)

# 基于朴素贝叶斯公式，计算单个对象的各类别概率，以概率最大的类别为预测类别，输出预测的类别
def predict(X):  # 只对每一行的X值进行计算，即预测每个对象的类别
    P_Y = []
    labels = list(datas_count.keys())
    for i in labels:  # 推荐类型
        P = 1
        P_i = datas_count[i][i]
        for j in X.index: # 所有特征
            """ 如果原数据中某个类型下没有某个特征值，则该类型下就没有X[j]这个键，
            那么获取datas_count[i][j][X[j]]键值时程序会报错：
            因此，需要捕获报错，在except中，将datas_count[i][j][X[j]]设置为0，再另行计算
            （也就是当找不到某个特征值，就赋值为0，而不是让程序报错）
            """
            try:
                μ = datas_count[i][j][0]

                σ = datas_count[i][j][1]
                x = X[j]
                if σ == 0:
                    P_x = 1

                P_x = 1/(math.sqrt(2*math.pi)*μ)*math.exp(-math.pow(x-μ,2)/(2*σ*σ))
                P *= P_x
                print(f"【{j}】值为{X[j]}，{i}人数为占比{round(P_x*100,6)}%")
            except:
                P_x = 1
                P *= P_x
                print(f"【{j}】值为{X[j]}，{i}人数为占比{round(P_x*100,6)}%")
        P_Y.append(round(P*P_i,8))
    # 获取概率最大的类别名称
    Y_hat = labels[P_Y.index(max(P_Y))]
    return Y_hat

# 应用了pandas中的apply函数，将每行数据都进行predict运算预测
Y_hat = X.apply(predict,axis = 1)

# print(f"分类准确率：{sum(Y==Y_hat)/len(Y)*100}%")

奇了怪了…怎么sklearn的高斯朴素贝叶斯分类准确率比我的还低呢。。。。
我这是将所有特征值，都用正态分布来计算概率的。。。。
不过也能看得出，朴素高斯贝叶斯，相对于朴素贝叶斯，好像分类结果比较差呢