S-DES加密算法

一、S-DES

S-DES 是一种简化版的数据加密标准。相对于 DES 来说，S-DES 更加简单、快速、高效，可以用于学习加密算法的入门课程。

二、加密和解密步骤

使用 S-DES 进行加密和解密的步骤如下：

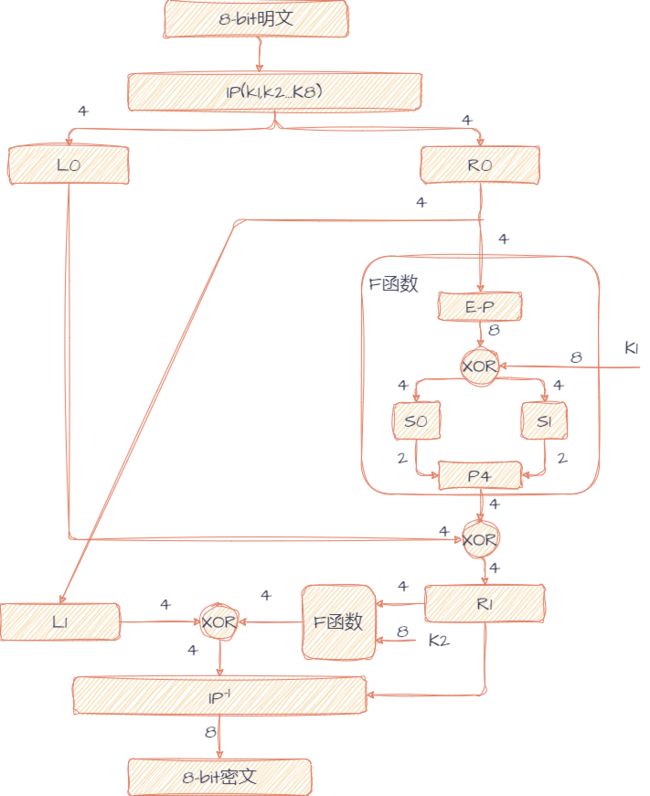
1. 初始置换（IP）
   • 将 8 位明文分为左右两部分，各 4 位，进行初始置换，得到置换后的左右两部分。
2. 轮函数（F）
   • 对置换后的右半部分进行扩展置换（E-P），将其扩展为 8 位。
   • 将扩展后的结果与轮密钥 K1 进行异或运算，再将异或的结果拆分成 2 个 4 位的块。
   • 将这 2 个块分别通过 S 盒代替（S0 和 S1），然后再进行 P4 置换，最后将 P4 置换后的结果与左半部分进行异或，得到 F 函数输出的结果。

S盒运算规则(具体见案例)：

• 将第1和第4的输入比特做2—bit数，指示为S盒的一个行；

• 将第2和第3的输入比特作为S盒的一个列;

• 其中S0查表需要E-P和K的异或的结果的前4位，S1为后4位。

• 如S1=1101 ，第1个数和第四个数代表要查的行，第2个数和第3个数代表要查的列，即11行(第3行)，第10列(第2列)，查询矩阵的结果是1，即01。

注意矩阵的起始行列都是第0行(列)

3. 轮秘钥生成

   • 根据初始密钥生成 2 个 8 位的密钥（K1 和 K2）。
   • 首先对初始密钥进行 P10 置换，并将置换后的结果分为左右两部分，各 5 位。
   • 接下来对左右两部分进行循环左移，得到移位后的结果。

   • 最后将左右两部分合并，并进行 P8 置换，得到 K1。

   • 对 K1 进行循环左移，并进行 P8 置换，得到 K2。

4. 加密和解密
   • 将明文通过初始置换（IP）得到左右两部分。
   • 然后进行 2 轮加密/解密操作，每轮操作包括以下步骤：
     • 将右半部分作为输入，通过 F 函数得到输出。
     • 将 F 函数的输出与左半部分进行异或运算，得到新的右半部分。
     • 将原来的右半部分作为新的左半部分。
     • 如果是加密操作，则使用 K1 进行第一轮加密，使用 K2 进行第二轮加密；如果是解密操作，则使用 K2 进行第一轮解密，使用 K1 进行第二轮解密。
     • 将左右两部分交换，再进行一次初始置换逆置换（$I{P}^{-1}$)，得到密文或明文。

三、案例

1. 密钥生成

问题描述：S-DES加密，$密匙K=(10100,00010),P10=(3,5,2,7,4,10,1,9,8,6),P8=(6,3,7,4,8,5,10,9)则K1,k2$分别为？

1. 计算P10后的密匙

$K(P10)$:10100 00010 (3,5,2,7,4 10,1,9,8,6)=10000 01100

2. 计算$K1$

左四位、右四位$LS-1$后合并：00001 11000

$K1(P8)$:00001 11000 (6,3,7,4, 8,5,10,9)=1010 0100

3. 计算$K2$

在已经$LS-1$的基础上$LS-2$: 00100 00011

$K2(P8)$:00100 00011(6,3,7,4, 8,5,10,9)=0100 0011

2. 进行S-DES加密

已知:$明文P=(1011,0101),IP=(2,6,3,1,4,8,5,7),E-P=(4,1,2,3,2,3,4,1),P4=(2,4,3,1),I{P}^{-1}=(4,1,3,5,7,2,8,6),k1,k2是上方计算的值$。
S 0 = [ 1 0 2 3 2 3 0 1 0 1 3 2 3 2 1 0 ] S0=\begin{bmatrix} 1&0&2&3\\ 2&3&0&1\\ 0&1&3&2\\ 3&2&1&0 \end{bmatrix} S0= ​1203​0312​2031​3120​ ​

S 1 = [ 0 1 2 3 2 0 3 1 1 3 0 2 3 2 1 0 ] S1=\begin{bmatrix} 0&1&2&3\\ 2&0&3&1\\ 1&3&0&2\\ 3&2&1&0 \end{bmatrix} S1= ​0213​1032​2301​3120​ ​

1. 第一轮

$P(IP)$:1011 0101 (2,6,3,1, 4,8,5,7)=0111 1100

$L0$:0111

$R0$:1100

$L1$:1100

$R0(E-P)$:1100 (4,1,2,3, 2,3,4,1)=0110 1001

$k1$:1010 0100

$XOR(R0与K1异或)$:0110 1101 XRO 1010 0100=1100 1101

$S0$:1100

$S1$:1101

经S盒规则(查S0和S1，行(列)起始为第0行(列))

$s0(1,4)(2,3)$，即s0矩阵第ob10行，第ob10列：0b11

$s1(1,4)(2,3)$，即s1矩阵第ob11行，第ob10列：0b01

$即P4(未变换)$:11 01

$P4(变换)$:1101 (2,4,3,1)=1101

$XOR(P4与L0异或)$:1101 XRO 0111=1010

$即R1$:1010

2. 第二轮

$R1(E-P)$:1010 (4,1,2,3 2,3,4,1)=0101 0101

$k2$:0100 0011

$XOR(R0与K1异或)$:0101 0101 XRO 0100 0011=0001 0110

$S0$:0001

$S1$:0110

经S盒规则

$P4(未变换)$:10 11

$P4(变换)$:1011 (2,4,3,1)=0111

$XOR(P4与L1异或)$:0111 XRO 1100=1011

$即R2$:1011

3. $I{P}^{-1}$得到密文

$密文=(R2+R1)(I{P}^{-1})$:1011 1010 (4,1,3,5 7,2,8,6)=1111 1000

四、安全性

虽然 S-DES 可以用于学习加密算法的入门课程，但它已经被证明不足以提供足够的安全性。具体来说，S-DES 存在以下安全问题：

1. 密钥长度过短：S-DES 使用的密钥长度只有 10 位，这使得它容易受到暴力破解攻击。
2. 线性结构：S-DES 的轮函数 F 是基于线性变换和置换操作的。由于线性变换可以被表示为矩阵乘法，因此 S-DES 可能会受到差分攻击和线性攻击等攻击方式的威胁。
3. 小型 S 盒：S-DES 使用的 S 盒只有 2 个，每个 S 盒只有 4 个输入和 2 个输出。这使得 S-DES 更容易受到差分攻击和线性攻击等攻击方式的威胁。

以上安全问题都对 S-DES 的安全性产生了影响，因此在实际中不建议使用 S-DES 进行加密。如果需要更强大和安全的加密算法，建议使用更先进的加密算法，比如 AES（Advanced Encryption Standard）。

五、Python实现

# 通用置换函数
def permute(input_str, table):
    output_str = ""
    for bit_position in table:
        output_str += input_str[bit_position - 1]
    return output_str


# 循环左移函数
def ls(key, n):
    # 将密钥分成两段并循环左移 n 位
    left_half = key[:5]
    right_half = key[5:]
    shifted_left = left_half[n:] + left_half[:n]
    shifted_right = right_half[n:] + right_half[:n]
    return shifted_left + shifted_right


# 子密钥生成
def generate_key(k, p10_table, p8_table):
    # 执行 P10 置换
    p10_key = permute(k, p10_table)
    # 对结果进行左移操作和P8置换，得到 K1
    k1 = permute(ls(p10_key, 1), p8_table)
    # 再次对上一步结果进行左移操作h和P8置换，得到 K2
    k2 = permute(ls(ls(p10_key, 1), 2), p8_table)
    return k1, k2


# S-DES 的 F 函数
def F(right_half, k):
    # 对右半部分进行 E/P 扩展置换
    expanded = permute(right_half, ep_table)
    # 对结果与 K1 进行异或操作
    xored = '{0:08b}'.format(int(expanded, 2) ^ int(k, 2))
    # 将结果分为两组，并根据 S-box 进行替换
    s0_input = xored[:4]
    s1_input = xored[4:]
    # 根据S盒规则行列查找
    s0_row = int(s0_input[0] + s0_input[-1], 2)
    s0_col = int(s0_input[1:-1], 2)
    s1_row = int(s1_input[0] + s1_input[-1], 2)
    s1_col = int(s1_input[1:-1], 2)
    s0_output = '{0:02b}'.format(sbox0[s0_row][s0_col])
    s1_output = '{0:02b}'.format(sbox1[s1_row][s1_col])
    # 对两个输出串进行 P4 置换得到最终结果
    s_output = s0_output + s1_output
    return permute(s_output, p4_table)


# 加密过程
def encrypt(p, k1, k2):
    # 执行初始置换
    p = permute(p, ip_table)
    # 进行两轮 Feistel 加密
    l0 = p[:4]
    r0 = p[4:]
    l1 = r0
    # 第一轮的P4
    f_result = F(r0, k1)
    # p41和L0异或
    r1 = '{0:04b}'.format(int(l0, 2) ^ int(f_result, 2))
    # 第二轮的P4
    f_result = F(r1, k2)
    # p42和L1异或
    r2 = '{0:04b}'.format(int(l1, 2) ^ int(f_result, 2))
    # 逆置换并返回结果(左边R2右边R1)
    return permute(r2 + r1, ip_ni_table)


# 解密过程
def decrypt(c, k1, k2):
    # 执行初始置换
    c = permute(c, ip_table)
    # 进行两轮 Feistel 解密（注意子密钥的使用顺序）
    r2 = c[:4]
    l2 = c[4:]
    # 第一轮的P4
    f_result = F(l2, k2)
    # p41和R2异或
    l1 = '{0:04b}'.format(int(r2, 2) ^ int(f_result, 2))
    # 第二轮的P4
    f_result = F(l1, k1)
    # p42和R1异或
    r1 = '{0:04b}'.format(int(l2, 2) ^ int(f_result, 2))
    # 逆置换并返回明文
    return permute(r1 + l1, ip_ni_table)


# 测试

# 密钥key、明文p、各个置换、S盒
key = "1010000010"
p10_table = (3, 5, 2, 7, 4, 10, 1, 9, 8, 6)
p8_table = (6, 3, 7, 4, 8, 5, 10, 9)
p4_table = (2, 4, 3, 1)
p = "10110101"
ip_table = (2, 6, 3, 1, 4, 8, 5, 7)
ep_table = (4, 1, 2, 3, 2, 3, 4, 1)
ip_ni_table = (4, 1, 3, 5, 7, 2, 8, 6)
sbox0 = [
    [1, 0, 2, 3],
    [2, 3, 0, 1],
    [0, 1, 3, 2],
    [3, 2, 1, 0]
]

sbox1 = [
    [0, 1, 2, 3],
    [2, 0, 3, 1],
    [1, 3, 0, 2],
    [3, 2, 1, 0]
]

# 生成子密钥 K1 和 K2
k1, k2 = generate_key(key, p10_table, p8_table)

# 对明文进行加密
ciphertext = encrypt(p, k1, k2)
# 对密文进行解密
plaintext = decrypt(ciphertext, k1, k2)

# 输出解密结果
print("明文P：", p)
print("密钥K：", key)
print("子密钥k1：", k1)
print("子密钥k2：", k2)
print("密文：", ciphertext)
print("解密后的明文：", plaintext)

六、运行截图