【C语言篇】函数递归详解+汉诺塔问题、小青蛙跳台阶实例详解+浅谈递归优缺点

1，递归定义

在一个函数体中，直接或间接的调用了这个函数本身。分为直接递归调用和间接递归调用

图解：1,直接递归调用：即函数体内部又调用了本身

void test()
{
	...
	test();
	...
}
int main()
{
	...
	test();
	return 0;
}

这只是简单演示，test函数执行，在函数体内部又调用test(）函数，如此形成一个类似与循环的过程。（当然，这里肯定要有让“循环”停下来的条件，这也是下面会讲到的–递归出口）；

图解2：间接递归调用：

和直接递归调用不同，间接会设计到多个函数，如这里，add()函数执行的过程中会调用到test函数，而在test函数执行的过程中又调用add()函数，如此，也是一个“循环”的过程。

void add();//add的声明
void test()
{
	...
	add();
	...
}
void add()
{
	...
	test();
	....
}
int main()
{
	add();
	return 0;
}

2， 用递归解决求阶乘问题–详解

当然，在讲递归使用条件之前，我们用一个具体使用递归来解决问题的例子，去感受一下递归，从而更好的理解下面会总结的递归使用的条件和递归的注意事项。

问题：运用函数递归，求n 的阶乘

是不是看起来so easy！

#include<stdio.h>
int Fac(int n)
{
		return n * Fac(n - 1);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fac(n);
	printf("%d",ret);
	return 0;
}

but…这样就行了吗？
no,no,no!!!
上面说到，递归其实类似与循环，那么我们联想一下循环，如果没有跳出循环的条件，循环是不会终止的。递归也一样，如果没有让递归停止下来的条件，也会是一个死递归。
再回过头来看这个代码，递归终止的条件是什么？或者说，递归终止的条件是什么？
是不是当n=1?Yes.你的n-1不可能无限进行下去，当n=1，也就是最简单的情况下（不需要由前面的小规模问题推导而来），是不是直接是return 1就好了。
那么我们来修改一下代码：

#include<stdio.h>
int Fac(int n)
{
	if (n == 1)
	{
		return 1;
	}
	else
		return n * Fac(n - 1);
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fac(n);
	printf("%d",ret);
	return 0;
}

我们用图解，来详细剖析一下这个递归进行的过程：

由上面这个例子，相信大家对递归应该有那么点感觉了吧
没关系，接下来我们看看对递归条件的具体描述，结合起来加深印象

3，递归调用的条件：

：我们需要解决的问题，可以转化为与这个问题解决思路（or叫做方法，其实函数就是一种解决问题的方法）相同，但规模较小的问题来解决。（大事化小）
：存在最简单的一种情况（这种情况无需转换为比它规模更小的问题），或者说规模最小的情况，使递归在这种情况下结束。（更准确来说，是从“递”的过程，转为“归”过程。

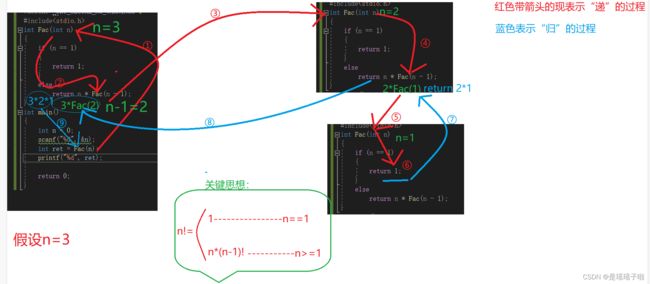
这里继续对上面求阶乘问题分析：
①：是否满足A?
n!可以转换为n*(n-1)!,fac(n)是来求n的阶乘的，那么fac(n)同样可以求n-1的阶乘，所以就把求n!转换为求(n-1)!,而(n-1)!=(n-1)*(n-2)!..由此，把一个规模较大的问题，层层转化为规模较小的问题解决。A满足✅
②：是否满足B？
当n=1时，n!==1.存在这么一个最简单，规模最小的问题，B满足✅

❗注意：在使用递归时，必须存在这么一个if语句，放在最前面，来判断最小规模情况是否满足，保证函数在递归进行过程中能够即时检测最小规模情况是否满足以终止递归调用。

递归经典实例：

汉诺塔问题：

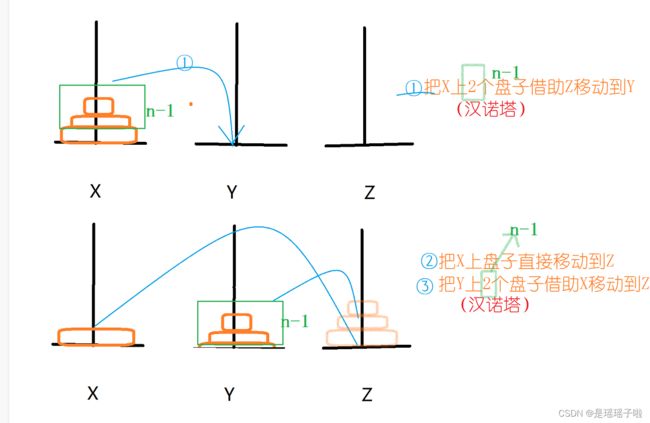
问题简述：X柱子上由n个盘子，从上到下盘子按从小到大顺序排。先要把X上面的盘子移动到Z柱子上，且只有一个柱子Y可以借助。每次只能移动一个盘子，而且不管在哪个柱子上，从上到下，盘子都是依次增大的排列。

其实实际分析的我们很难一下子从A条件入手，反而是先从B条件–最小规模入手。
思路：
1，假设n==1,只需要一步：X–>Z

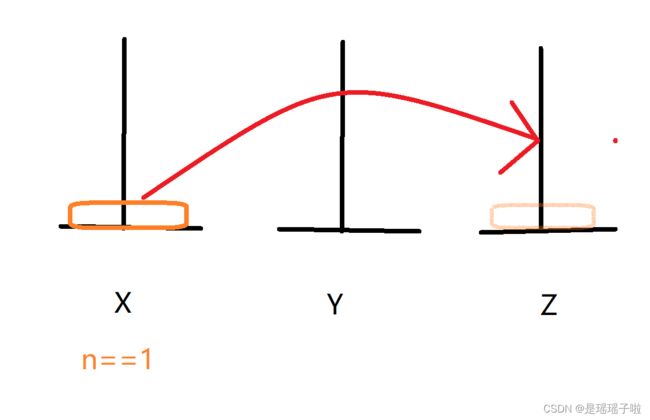
2,n = =2,(把X上两个盘子借助Y以汉诺塔的方式移动到Z）

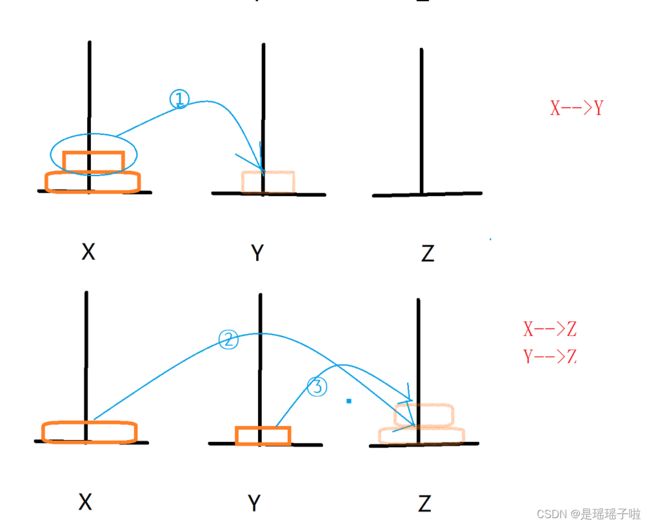
3,其实当n= =2的时候，将最上面哪个盘子从X移动到Y可以看作：怎么样先将一个盘子借助Z移动到Y（缩小到1个盘子的汉诺塔问题），再将一个盘子从X借助Y移动到Z，最后将一个盘子从Y借助X移动到Z（汉诺塔来实现）。
4，n= =3

4，大事化小

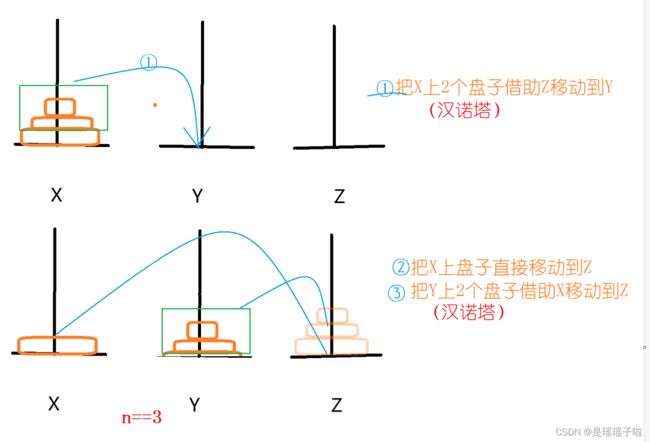
综上，汉诺塔是适用于递归的：
①：是否满足条件A？✅
为n时可以化为三步骤：
ⅰ：将X上n-1个借助Z以汉诺塔方式移动到Y
ⅱ：将X上剩下的一个直接移动到Z
ⅲ：将Y上n-1个借助X以汉诺塔方式移动到Z
②：是否满足条件B？✅
当n= =1时为最小规模，直接从X–Z

代码实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
void move(char x, char z)
{
	printf("%c--->%c\n",x,z);
}
void Hanoi(int n, char x, char y, char z)
{
	if (n == 1)
	{
		move(x, z);//表示把盘子从X移动到Z
	}
	else
	{
		Hanoi(n - 1, x, z, y);//把X上的n-1个盘子借助Z移动到Y上
		move(x, z);//把X上剩下的那一个直接移动到Z
		Hanoi(n - 1, y, x, z);//把Y上n-1借助X移动到Z上

	}
}

int main()
{
	int n = 0;
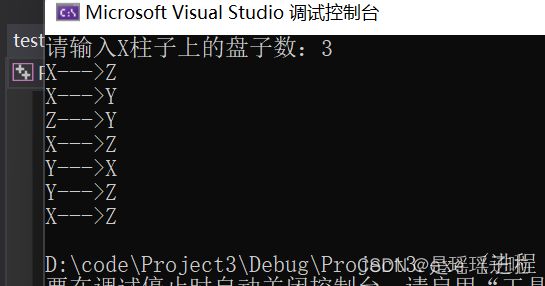
	printf("请输入X柱子上的盘子数：");
	scanf("%d", &n);
	char x = 'X';
	char y = 'Y';
	char z = 'Z';
	Hanoi(n, x, y, z);//表示将X柱子上的n个元素借助Y移动到Z

	return 0;
}

结果：

小青蛙跳台阶

问题简述：小青蛙每次跳台阶有可能一次跳一步，也有可能跳两步，假设有n个台阶，问有多少种跳法。

思路：
1，n= =1。只有1种跳法
2，n= =2。2种跳法（一步一步跳，或者直接跳两步）
3，n==3。
如果青蛙先跳一步，则还有2个台阶（加上小青蛙跳2个台阶的方法数）。如果先跳两步，则还有1个台阶（为小青蛙跳1个台阶的方法数）
3，n= =4.
方法数等于：青蛙跳3个台阶的方法数（假设先跳1步）+ 青蛙跳2个台阶方法数（先跳了两步）。
… …

综上，也是可以满足递归的：
①：是否满足条件A？✅
青蛙跳n个台阶的方法数= =青蛙跳n-1个台阶的方法数 + 青蛙跳n-2个台阶的方法数。
②：是否满足条件B？✅
当n= =1时，方法数为1.
当n= =2时，方法数位2.

代码实现：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int jump_ways(int n)
{
	if (n == 1)
	{
		return 1;
	}
	if (n == 2)
	{
		return 2;
	}
	else
	{
		return jump_ways(n - 1) + jump_ways(n - 2);
	}

}

int main()
{
	int n = 0;
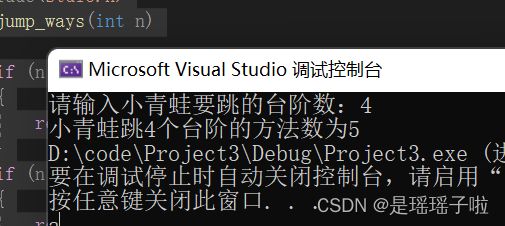
	printf("请输入小青蛙要跳的台阶数：");
	scanf("%d", &n);
	int ret = jump_ways(n);
	printf("小青蛙跳%d个台阶的方法数为%d", n, ret);
	return 0;
}

浅谈递归优缺点：

递归优点：

代码简洁，易于理解，大事化小

递归缺点：

1，时间和空间消耗大。递归是函数调用自身，每次函数调用，都会给形参、函数体内局部变量、返回值开辟新的内存空间，当递归次数过高时，内存空间占用过大。而往内存种写入和读取数据都需要时间。
2，重复计算。递归的本质是把一个大问题分解成两个或者多个小问题，小问题在计算的过程中存在重叠部分，比如算n的阶乘。
3，当占用空间过于大时，会导致内存溢出。

其实能用递归写出来的大多数都能用循环写出。

---

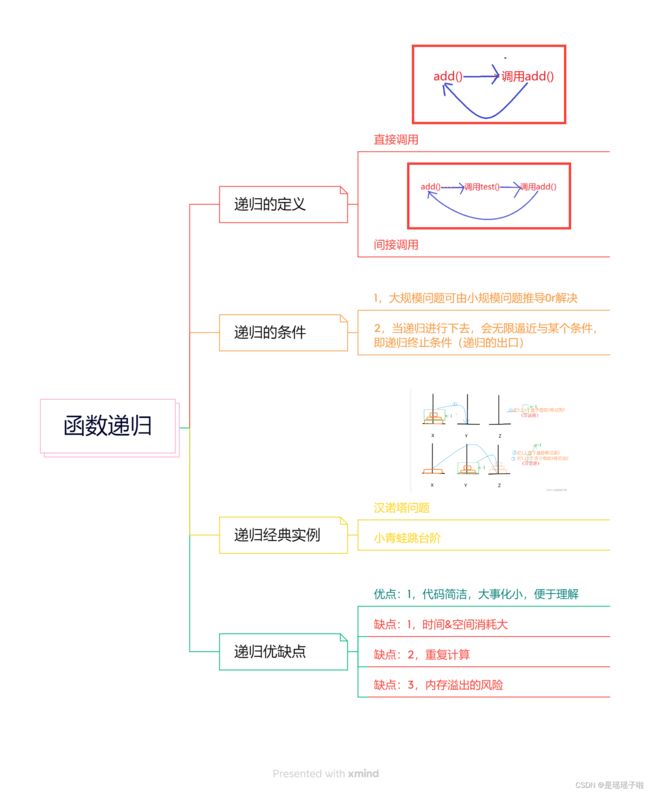
思维导图-总结

总之，递归虽好，可不要贪杯哦~(●ˇ∀ˇ●)