一文看懂B TREE和B+TREE数据结构实现过程及数据存储结构
概述
一文看懂B TREE和B+TREE数据结构实现过程及数据存储结构
一、B tree数据结构实现过程
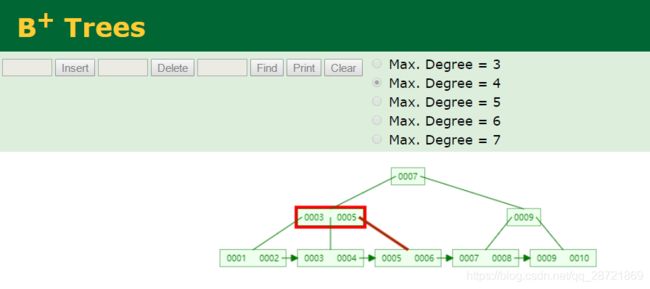
这里有一个陌生区关于 Max. Degree，这个你可以理解为阶，也可以理解为度,即B+ 树的阶数（一个节点存储的键的数量）
这里有一个陌生区关于 Max. Degree，这个你可以理解为阶，也可以理解为度,即B+ 树的阶数（一个节点存储的键的数量）
1、插入数据
现在可以看到目前只插入了 3 条数据：
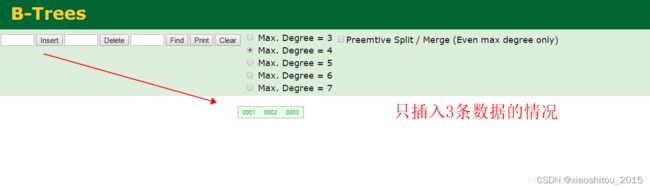再加一条数据，节点就会进行分裂，这个也就验证了当阶设置为 n 时，一个节点可存 n-1 条数据
想要达到快速检索数据，那就需要满足俩个特性，一个是有序，另一个就是平衡。
从下图中可以看到 BTree 是有一定的顺序性的，平衡性更满足
2、查找数据
查找数据为9的过程如下：
当查找数值9，首先看到的数据是 4，9 是大于 4 的，所以会往 4 的右节点寻找。继续找到范围在 6 到 8 的节点，9 又大于 8，所以还需要往右节点寻找，最有一步就找到了数据 9，这个过程就是 BTree 数据结构查找数据的执行过程。
查找数据为6的过程如下：
当查找数值6，首先看到的数据是 4，6 是大于 4 的，所以会往 4 的右节点寻找。继续找到范围在 6 到 8 的节点，然后就找到了数据6，此时只需要2次IO。
3、删除数据
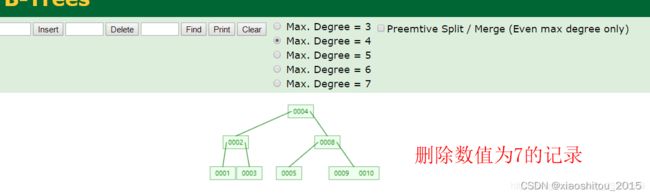
假设删除数据为6的记录，过程如下：
删除数据为7的记录，过程如下：
二、Btree数据存储
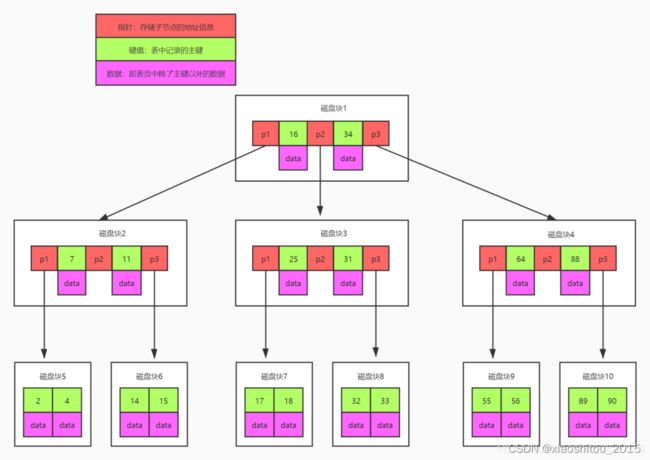
在下图中 P 代表的是指针，指向的是下一个磁盘块。在第一个节点中的 16、24 就是代表我们的 key 值是什么。date 就是这个 key 值对应的这一行记录是什么。
假设寻找 key 为 33 的这条记录，33 在 16 和 34 中间，所以会去磁盘 3 进行寻找。
在磁盘 3 中进行判断，指针指向磁盘 8。在磁盘 8 中即可获取到数据 33，然后将 data 返回。
一般说到的页都是数据页。默认的页面大小为16kb，每个页中至少存储2条或以上的行记录。那么根据 BTree 数据查找的过程中可以得知一共读取了三个磁盘，那么每个磁盘的大小就是 16kb。
而目前的给的案例寻找了三层，那么三层存储的数据就是：16kb16kb16kb=4096kb。
如果按照一条记录所需内存 1kb，那么这三层的 BTree 就可以存储 4096 条记录。
数据库的数据少则几百万，多则几千万数据，那么 BTree 的层级就会越来越深，相对的查询效率也会越来越慢。
这里就要考虑为什么在 Btree 中 48kb 的内存怎么就只能存储 4000 多条记录？
问题就出现在 data 上，要知道在计算数据大小时指针地址和 key 的内存都是没有计算在内的，单单就计算了 data 的内存。
问题就出现在 data 上，要知道在计算数据大小时指针地址和 key 的内存都是没有计算在内的，单单就计算了 data 的内存。
三、B+ Tree数据结构实现过程
1、插入数据
可以看到目前只插入了 3 条数据：
再插入一条数据
共插入十条记录，结构如下：
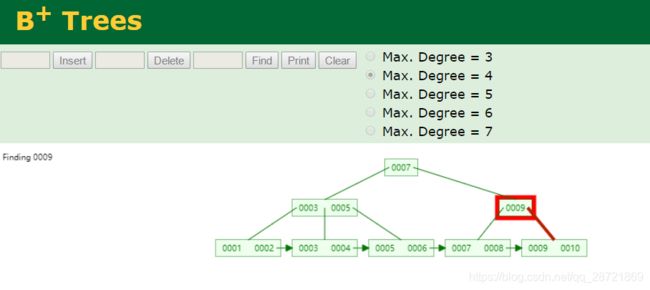
2、查找数据
当查找数值9，首先看到的数据是 4，9 是大于 4 的，所以会往 4 的右节点寻找。继续找到范围在 6 到 8 的节点，9 又大于 8，所以还需要往右节点寻找，最有一步就找到了数据 9，这个过程就是 B+Tree 数据结构查找数据的执行过程。
演变过程如下：
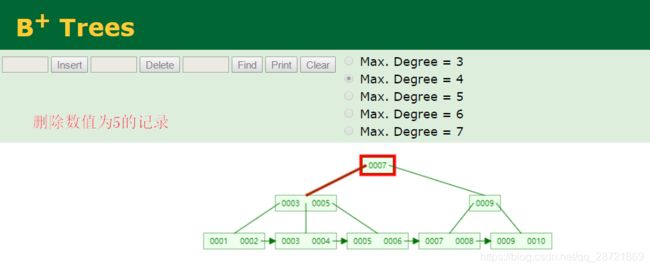
当查找数值为5的过程，如下：
当查找数值5，首先看到的数据是 7，5 是小于 7 的，所以会往 7 的左节点寻找。继续找到范围在 3 到 5 的节点，然后再往右节点寻找，最后在叶子结点找到了数据 5，总共需要3次IO。
3、删除数据
假设删除数据为6的记录，过程如下：
四、B+Tree存储
对比B树的数据存储结构可以看到：
- 对比B树的数据存储结构可以看到：
- B+Tree 所有的叶子节点之间是一种链式环结构。
那么在这个过程中到底读取了多少条数据呢？
假设B+Tree 读取数据的深度跟 B-Tree 的深度一样，都是三层，那么同样的道理每个磁盘的大小为 16kb。
那在 B+Tree 中非叶子节点可以存储多少数据呢？一般来说我们每个表都会存在一个主键。
根据三层来计算，第一层跟第二层存储的是 key 值，也就是主键值。
由于 int 类型所占的内存是 4Byte（字节），指针的存储就给个 6Byte，一共就是 10Tybe，那么第一层节点就可以存储 161000/10=1600。
同理第二层每个节点也是可以存储 1600 个 key。
第三层是叶子节点，每个磁盘存储大小同样安装 BTree 的计算一样，每条数据占 1kb。
**那么在 B+Tree 中三层可以存储的数据就是 16001600*16=40960000。**
从这点来看 B+Tree 存储的数据跟 BTree 存储的数据根本就不是一个级别，这样大家就知道为什么MySQL数据库要用B+树了吧~
原文: