经验模态分解与Python调用实例

经验模态分解

如果需要对一个信号进行降噪的话，我们通常会尝试将一个时域信号变换到不同的域空间，以期将信号中的噪声和有效信号在该域空间分开。比较熟悉的滤波器方法、小波分解去噪甚至空间滤波方法都是这样。在这篇博客里所阐述的经验模态分解方法也是如此，将含噪声信号分解为数个本征模态函数（IMF）和残差（Res）。相比于其他的分解方法，经验模态分解具有更强的适应性，也非常适合对于非平稳信号的分析。
IMF需要满足极值个数与过零点个数相等或相差至多一个，且由极值和极值定义的包络线的均值必须为零。该算法无需预先设定任何基函数，仅依据自身的时间尺度特征进行信号分解。分解过程如下：
设原始数据为$x[n]$

1. 找到信号所有的极大值与极小值，并分别使用三次采样插值连接它们，获得上包络$u[n]$和下包络$l[n]$。
2. 计算平均值$\mu [n]=(u[n]+l[n])/2$，并从原始值中减去$b[n]=x[n]-\mu [n]$。
3. 根据预设条件判断$b[n]$是否为IMF。
4. 如果不是，用$b[n]$代替$x[n]$，直到$b[n]$满足判据，则$b[n]$就是需要提取的IMF，记$b_k[n]$。
5. 每获得一阶IMF就从原信号中减去它，直到剩余部分$r[n]$为单调序列或常值序列。
   原始信号就可以被分解为：

$$x[n]=\sum _{k=1}^m{b}_k[n]+r[n]$$
确定分解后的信号后就可以选择并去除伪影分量，然后使用新的IMF重构出纯净的EEG数据。
经验模态分解也有许多改进的算法，例如集成经验模态分解（EEMD），该算法通过给待分解信号加入随机噪声来增强分解的稳定性和可靠性，提升信号分解的质量，下面我将使用该算法实现对于一段音频信号的分解。

Python代码实现

使用的音频文件是一段从网上下载的语音，文件名为1654855780977898.wav
想在Python中使用经验模态分解，我们需要使用一个专用的经验模态分解包PyEMD。可以通过下面的语句进行安装：

pip install EMD-signal

安装完成后，我们开始正式的示例展示：
首先导入相关包：

import visualization
from scipy.io import wavfile
from PyEMD import EEMD
import numpy as np

不必好奇这里的visualization是什么，这是我自己写的文件，封装了用于绘图展示的函数，相关文件会在后面给出。
接下来将音频文件读入：

data = wavfile.read('1654855780977898.wav')

打印data变量：

这是一个元组变量，第一个是该音频的采样率，第二个是一个（time*freq，2）形状的二维ndarray对象数据类型是int16，第二个维度代表左右声道。
接下来，将整型变换为浮点数类型（别问为啥，我也是看别人这么用的），并分离左右声道，截取最后两秒的声音即可：

dataT = data[1].T
left = dataT[0] / 32768
right = dataT[1] / 32768
left = left[-22050:]
right = right[-22050:]

绘图展示一下左声道时域波形：

visualization.plot_time_field(left,0,2,11025,figsize=(7,7))

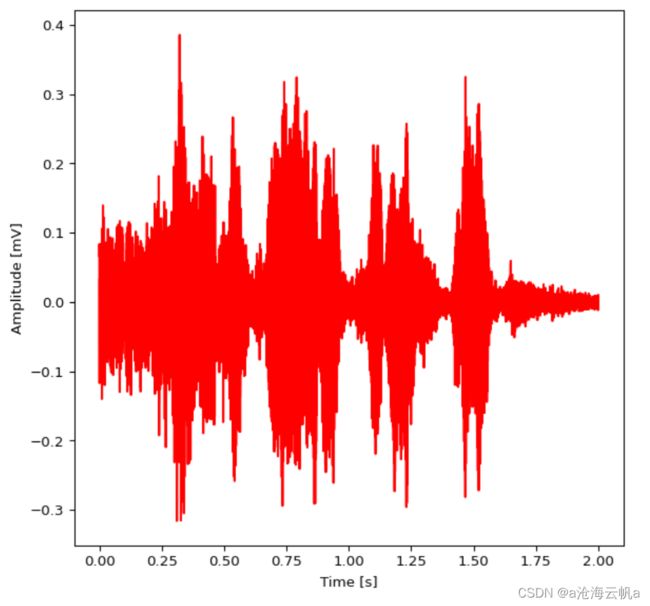
好，接下来开始使用EEMD分解，需要先实例化一个EEMD对象再调用该方法：

eemd = EEMD()
IMFl = eemd.eemd(left,max_imf=7)
IMFr = eemd.eemd(right,max_imf=7)

max_imf用于限制分解的本征模态函数（大部分情况下并不需要分解到最后，因为高频噪声都在前面）。
绘图看看左声道的：

visualization.plot_emd(left,IMFl,0,2,11025)

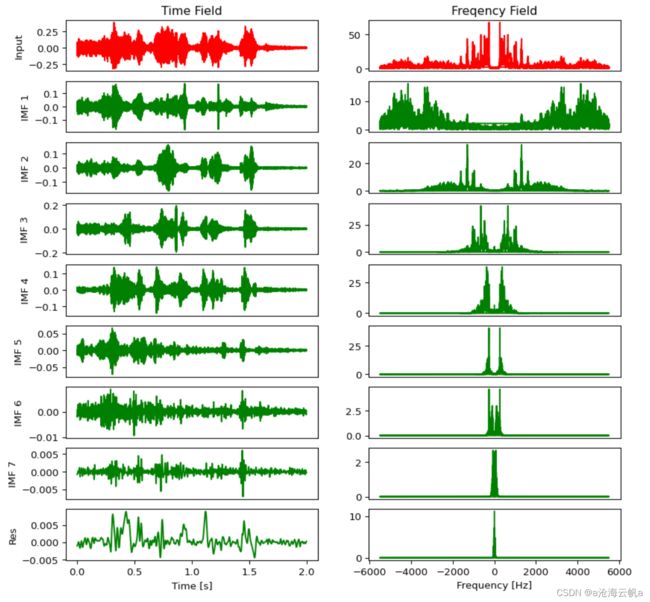
左边是原始信号和本征模态函数的时域图像，右边是频域图像（这里我自己写了一个函数，因为PyEMD给出的官方示例是有点子难看在身上的）。可以很明显的看到前面的本征模态分量集中在高频部分。
然后可以用各本征模态分量重建出各分量对应的音频：

wave1 = np.concatenate((IMFl[0,np.newaxis],IMFr[0,np.newaxis]),axis=0)
wave1.shape

wave1 *= 32768
wave1 = wave1.T

wavfile.write('1.wav',11025,wave1.astype(np.int16))

（用几个分量来重建也行）

最后，分享我所用的visualization里面的各个函数。使用的话请单独创建一个.py文件：

import matplotlib.pyplot as plt
from scipy import fft
import numpy as np
from PyEMD import EEMD
from PyEMD import EMD

def plot_time_field(data, begin, end, sample_freq, color='r', dpi=96, figsize=(10,10), file=None):
    '''
    绘制时域图
    '''
    t = np.arange(begin, end, 1 / sample_freq)
    plt.figure(figsize=figsize,dpi=dpi)
    plt.plot(t, data,color=color)
    plt.xlabel('Time [s]')
    plt.ylabel('Amplitude [mV]')
    if file != None:
        plt.savefig(file, bbox_inches='tight')
    plt.show()

def plot_freq_field(data, sample_freq, dpi=96,color='r', figsize=(10,10), file=None):
    '''
    绘制频域图
    '''
    xf = fft.fftfreq(sample_freq, 1 / sample_freq)
    dataf = fft.fft(data, sample_freq)
    plt.figure(figsize=figsize,dpi=dpi)
    plt.plot(xf,np.abs(dataf),color=color)
    plt.xlabel('frequency [Hz]')
    plt.ylabel('Amplitude')
    if file != None:
        plt.savefig(file, bbox_inches='tight')
    plt.show()

def plot_emd(data, IMF, begin, end, sample_freq, figsize=(10,10), dpi=96, file=None):

    t = np.arange(begin, end, 1 / sample_freq)
    N = IMF.shape[0]+1
    xf = fft.fftfreq(sample_freq, 1 / sample_freq) 
    dataf = fft.fft(data, sample_freq)   

    # Plot results
    plt.figure(figsize=figsize,dpi=dpi)
    plt.subplot(N, 2, 1)
    plt.plot(t, data, 'r')
    plt.title("Time Field")
    plt.ylabel("Input")
    plt.xticks([])

    plt.subplot(N, 2, 2)
    plt.plot(xf, np.abs(dataf), 'r')
    plt.title("Freqency Field")
    plt.xticks([])


    for n, imf in enumerate(IMF[0:-1]):
        plt.subplot(N, 2, (n+1)*2+1)
        plt.plot(t, imf, 'g')
        plt.ylabel("IMF "+str(n+1))
        plt.xticks([])

        plt.subplot(N, 2, (n+1)*2+2)
        imff = fft.fft(imf, sample_freq)
        plt.plot(xf, np.abs(imff), 'g')
        plt.xticks([])

    # Plot res
    plt.subplot(N, 2, 2*N-1)
    plt.plot(t, IMF[-1], 'g')
    plt.xlabel('Time [s]')
    plt.ylabel('Res')
    
    plt.subplot(N, 2, 2*N)
    resf = fft.fft(IMF[-1], sample_freq)
    plt.plot(xf, np.abs(resf), color='g')
    plt.xlabel("Frequency [Hz]")

    if file != None:
        plt.savefig(file,  bbox_inches='tight')
    plt.show()


if __name__ == '__main__':
    t = np.arange(0,1,1/400)

    data = np.sin(2*np.pi*30*t)+np.cos(2*np.pi*10*t)+t*t

    plot_time_field(data, 0, 1, 400, dpi=100, file='time.jpg')
    plot_freq_field(data, 400, dpi=100, file='freq.jpg')

    emd = EMD()
    IMF = emd.emd(data,max_imf=6)
    plot_emd(data, IMF, 0, 1, 400, dpi=100, file='emd.jpg')
    data_denoise = eemd_denoise(data,num=[-1])
    plot_time_field(data_denoise, 0, 1, 400, dpi=100, file='time.jpg')
    plot_time_field(data-data_denoise, 0, 1, 400)

想要听一下原始音频和重建的音频，可以前往微信公众号——编码矩阵。