力扣动态规划专题（三）完全背包 多重背包 背包总结 518.零钱兑换II 377. 组合总和 Ⅳ 70. 爬楼梯 322. 零钱兑换 279.完全平方数 139.单词拆分 步骤及C++实现

完全背包

完全背包的物品数量是无限的，01背包的物品数量只有一个
完全背包和01背包分许步骤一样，唯一不同就是体现在遍历顺序上

有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品都有无限个，也就是一个物品可以放入背包多次，求解将哪些物品装入背包里物品价值总和最大。

背包最大重量为4，问物品有无限个，那么背包能背的物品最大价值是多少？物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

一维dp数组 滚动数组

1. 确定dp数组以及下标的含义：一维数组dp[j]，容量为j的背包，所背的物品价值可以最大为dp[j]

背包重量j	0	1	2	3	4
物品0
物品1
物品2

2. 确定递推公式，有两个方向推出来dp[j]：

• 不放物品i：由dp[j]本身推出，物品i的重量 > 背包j的重量，物品i无法放进背包中，背包内的价值不变。
• 放物品i：由dp[j - weight[i]] + value[i]推出，物品i的重量 < 背包j的重量，物品i可以放进背包中，背包内的价值为dp[j - weight[i]] + value[i]
• 递归公式： dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

4. dp数组如何初始化
   情况1：j=0时，dp[0]=0，此时背包容量j为0，无论选取什么物品，背包价值总和为0
   情况2：j≠0时，dp[j]会被覆盖更新。

背包重量j	0	1	2	3	4
物品0	0	15	15	15	15
物品1	0
物品2	0

4. 确定遍历顺序
   和01背包最大区别在于遍历顺序

1. 遍历顺序

• 01背包的二维dp数组的内外for循环遍历顺序可以互换，先遍历物品或者先遍历背包
• 01背包的一维dp数组的外层for循环只能先遍历物品，内循环遍历背包。且内循环从大到小遍历，为了保证每个物品仅被添加一次
• 纯完全背包的一维dp数组内外for循环遍历顺序也可以互换，并且完全背包的物品是可以添加多次的，所以要从小到大去遍历
• 不是纯完全背包，内外for循环不可以互换，如题518

//01背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

//完全背包 先遍历物品，再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
    for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
}

//完全背包 先遍历背包，再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
    }
    cout << endl;
}

5. C++实现

void test_CompletePack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    int bagWeight = 4;
    vector<int> dp(bagWeight + 1, 0);
    // 先遍历物品，在遍历背包
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }
    /*
    // 先遍历背包，再遍历物品
    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
        for(int i = 0; i < weight.size(); i++) { // 遍历物品
            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
    }*/
    cout << dp[bagWeight] << endl;
}
int main() {
    test_CompletePack();
}

518.零钱兑换II

注意题目说的是组合数，5 = 2 + 2 + 1与5 = 2 + 1 + 2是同一种组合，但是两种排列。

如果求组合数就是外层for循环遍历物品，内层for循环遍历背包。

如果求排列数就是外层for循环遍历背包，内层for循环遍历物品。

步骤

1. 确定dp数组以及下标的含义
   dp[j]：凑成总金额j的货币组合数为dp[j]

2. 确定递推公式
   dp[j] 就是所有的 dp[j - coins[i]]（考虑coins[i]）的情况相加，递推公式：dp[j] += dp[j - coins[i]];
   组合问题推导公式都类似dp[j] += dp[j - nums[i]];

3. dp数组如何初始化
   j=0时，dp[0]=1，表示只能选coins[i]硬币，且dp[0]=1是递归公式的基础，否则后面推导的值都为0
   j≠0时，dp[j]=0，这样累计加dp[j - coins[i]]的时候才不会影响真正的dp[j]

4. 确定遍历顺序

• 外for循环遍历物品（钱币），内层for遍历背包（金钱总额），计算的是组合数，只有{1, 3}，不会出现{3, 1}
• 外for遍历背包（金钱总额），内层for循环遍历物品（钱币），计算的是排列数，会出现{1, 3} 和 {3, 1}两种情况
• 如果外循环遍历物品coins，内循环遍历背包amount，计算dp[4]的时候，结果集只有 {1,3} 这样的集合，不会有{3,1}这样的集合，因为conis遍历放在外层，3只能出现在1后面

5. 举例推导dp数组
   输入: amount = 5, coins = [1, 2, 5]
   

6. C++实现

class Solution {
public:
    int change(int amount, vector<int>& coins) {
        vector<int> dp(amount+1, 0);
        dp[0] = 1;//初始化
        //组合数 先物品coins 后背包amount
        for(int i=0; i<coins.size(); i++)
        {
            for(int j=coins[i]; j<=amount; j++)
            {
                dp[j] += dp[j-coins[i]];
            }
        }
        return dp[amount];
    }
};

377. 组合总和 Ⅳ

注意题目说顺序不同的序列被视作不同的组合，求的是排列数，那么外层for遍历背包，内层for循环遍历物品。

如果要把所有排列都列出来，只能使用回溯算法

步骤

1. 确定dp数组以及下标的含义
   dp[i]：凑成目标正整数为i的排列个数为dp[i]

2. 确定递推公式
   dp[i]（考虑nums[j]）可以由 dp[i - nums[j]]（不考虑nums[j]） 推导出来，递推公式：dp[j] += dp[j - nums[i]];
   组合问题推导公式都类似dp[j] += dp[j - nums[i]];

3. dp数组如何初始化
   i=0时，dp[0]=1，没有意义，仅为了避免后面推导的值都为0
   i≠0时，dp[i]=0，这样累计加 dp[i - nums[j]] 的时候才不会影响真正的 dp[i]

4. 确定遍历顺序

• 外for循环遍历物品，内层for循环遍历背包，计算的是组合数——518题、494题
• 外for循环遍历背包，内层for循环遍历物品，计算的是排列数——本题

5. 举例推导dp数组
   输入: target=4, nums = [1, 2, 3]
   

6. C++实现

class Solution {
public:
    int combinationSum4(vector<int>& nums, int target) {
        vector<int> dp(target+1, 0);
        dp[0] = 1;
        //排列数 先背包target 后物品nums
        for(int i=0; i<=target; i++)
        {
            for(int j=0; j<nums.size(); j++)
            {
                if(i-nums[j] >= 0 && dp[i] < INT_MAX - dp[i-nums[j]]) dp[i] += dp[i-nums[j]];
            }
        }
        return dp[target];
    }
};

70. 爬楼梯

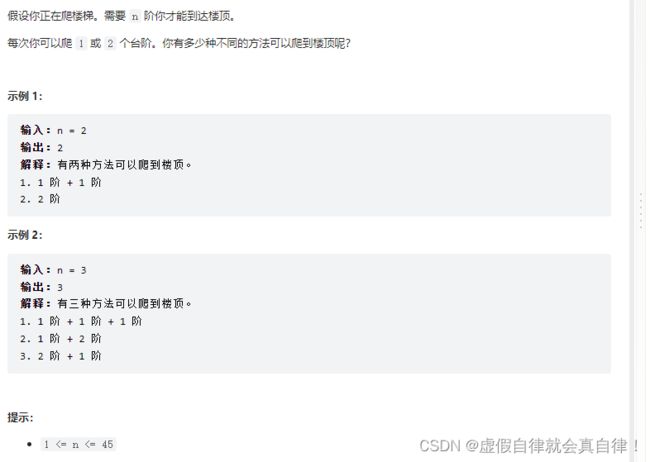
注意题目给的示例2中，1阶+2阶 和 2阶+1阶 是不同的组合，求的是排列数，外层for遍历背包，内层for循环遍历物品。

步骤

1. 确定dp数组以及下标的含义
   dp[i]：爬到有i个台阶的楼顶，有dp[i]种方法

2. 确定递推公式
   dp[i] 由 dp[i - j] 推导出来，递推公式：dp[i] += dp[i - j];
   组合问题推导公式都类似dp[j] += dp[j - nums[i]];

3. dp数组如何初始化
   i=0时，dp[0]=1，避免后面推导的值都为0
   i≠0时，dp[i]=0，这样累计加 dp[i - j] 的时候才不会影响真正的 dp[i]

4. 确定遍历顺序

• 外for循环遍历物品，内层for循环遍历背包，计算的是组合数——518题、494题
• 外for循环遍历背包，内层for循环遍历物品，计算的是排列数——本题、377题

5. 举例推导dp数组
   输入: n=4
   

6. C++实现

class Solution {
public:
    int climbStairs(int n) {
        /*
        //01背包 1.只维护两个数值
        if(n <= 1) return n;
        int dp[3];
        dp[1] = 1;
        dp[2] = 2;
        int sum = 0;
        for(int i=3; i<=n; i++)
        {
            sum = dp[1] + dp[2];
            dp[1] = dp[2];
            dp[2] = sum;
        }
        return dp[2];

        //01背包 2.维护整个数组
        if(n <= 1) return n;
        vector dp(n+1);
        dp[1] = 1;
        dp[2] = 2;
        for(int i=3; i<=n; i++)
        {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];*/

        //完全背包
        vector<int> dp(n+1, 0);
        dp[0] = 1;
        //排列数 先背包 后物品 
        //内层for循环的2表示一次最多可以爬2层台阶
        for (int i = 1; i <= n; i++) { // 遍历背包
            for (int j = 1; j <= 2; j++) { // 遍历物品
                if (i - j >= 0) dp[i] += dp[i - j];
            }
        }
        return dp[n];
    }
};

如果题目改为：一步一个台阶，两个台阶，三个台阶，…，直到 m个台阶。问有多少种不同的方法可以爬到楼顶？

• 1阶，2阶，… m阶就是物品，楼顶就是背包。每一阶可以重复使用，跳了1阶，还可以继续跳1阶
• 问跳到楼顶有几种方法其实就是问装满背包有几种方法——完全背包
• C++实现时，可以把完全背包方法中的 内层for循环中的2改成对应的m

322. 零钱兑换

注意题目说每种硬币的数量是无限的，完全背包

步骤

1. 确定dp数组以及下标的含义
   dp[j]：凑足总额为j所需钱币的最少个数为dp[j]

2. 确定递推公式
   dp[j]（考虑coins[i]），由dp[j - coins[i]]推导而来，再加上一个钱币coins[i]，就是dp[j]
   同时，dp[j] 取所有 dp[j - coins[i]] + 1 中最小的，递推公式：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);

3. dp数组如何初始化
   j=0时，dp[0]=0，凑足总金额为0所需钱币的个数一定是0
   j≠0时，dp[j]=INT_MAX，dp[j]必须初始化为一个最大的数，否则在 min(dp[j - coins[i]] + 1, dp[j])比较中会被初始值覆盖

4. 确定遍历顺序

• 外for循环遍历物品，内层for循环遍历背包，计算的是组合数——518题、494题
• 外for循环遍历背包，内层for循环遍历物品，计算的是排列数——377题、70题
• 本题并不强调是组合数还是排列数，只需要钱币个数最小，是纯完全背包问题。因此先遍历物品或者先遍历背包，并且内循环正序遍历

5. 举例推导dp数组
   输入: coins = [1, 2, 5], amount = 5
   

6. C++实现

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int> dp(amount+1, INT_MAX);
        dp[0] = 0;
        //先物品 后背包
        for(int i=0; i<coins.size(); i++)
        {
            for(int j=coins[i]; j<=amount; j++)
            {
                if(dp[j - coins[i]] != INT_MAX) dp[j] = min(dp[j], dp[j-coins[i]]+1);
            }
        }
        //先背包 后物品
        /*for(int i=0; i<=amount;i++)
        {
            for(int j=0; j= 0 && dp[i - coins[j]] != INT_MAX) dp[i] = min(dp[i], dp[i-coins[j]]+1);
            }
        }*/
        if (dp[amount] == INT_MAX) return -1;
        return dp[amount];
    }
};

279.完全平方数

完全平方数就是物品（可以无限件使用），凑个正整数n就是背包，问凑满这个背包最少有多少物品，完全背包问题

步骤

1. 确定dp数组以及下标的含义
   dp[j]：和为j的完全平方数的最少数量为dp[j]

2. 确定递推公式
   dp[j]，由 dp[j - i * i] 推导而来，再加上1就是dp[j]

同时，dp[j] 取所有 dp[j - i * i] + 1 中最小的，递推公式：dp[j] = min(dp[j - i * i] + 1, dp[j]);

3. dp数组如何初始化
   j=0时，dp[0]=0
   j≠0时，dp[j]=INT_MAX，dp[j]必须初始化为一个最大的数，否则在 min(dp[j - coins[i]] + 1, dp[j])比较中会被初始值覆盖

4. 确定遍历顺序

• 外for循环遍历物品，内层for循环遍历背包，计算的是组合数——518题、494题
• 外for循环遍历背包，内层for循环遍历物品，计算的是排列数——377题、70题
• 题目并不强调是组合数还是排列数，纯完全背包问题。因此先遍历物品或者先遍历背包，并且内循环正序遍历——本题、322题

5. 举例推导dp数组
   输入: n = 5
   

6. C++实现

class Solution {
public:
    int numSquares(int n) {
        vector<int> dp(n+1, INT_MAX);
        dp[0] = 0;
        //先背包 后物品
        for(int i=0; i<=n; i++)
        {
            for(int j=1; j*j<=i; j++)
            {
                dp[i] = min(dp[i], dp[i-j*j]+1);
            }
        }
        
        //先物品 后背包
        /*for(int i=1; i*i<=n; i++)
        {
            for(int j=i*i; j<=n ;j++)
            {
                dp[j] = min(dp[j], dp[j-i*i]+1);
            }
        }*/
        return dp[n];
    }
};

139.单词拆分

物品：单词wordDict；背包：字符串s；单词能否组成字符串s：物品能否把背包装满；题目中可以重复使用字典中的单词，完全背包问题

步骤

1. 确定dp数组以及下标的含义
   dp[i] : 字符串长度为i的话，dp[i]为true，表示可以拆分为一个或多个在字典中出现的单词。

2. 确定递推公式
   如果确定dp[j] 是true，且 [j, i] 这个区间的子串出现在字典里，dp[i]是true，j < i
   递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) dp[i] = true

3. dp数组如何初始化
   i=0时，dp[0]=true
   i≠0时，dp[i]=false，只要没有被覆盖说明都是不可拆分为一个或多个在字典中出现的单词。

4. 确定遍历顺序
   组成字符串之间有顺序，求的是排列数，先遍历背包，再遍历物品。例如，“apple”, “pen” 是物品，“applepenapple"只能由 “apple” + “pen” + “apple” ，不能是"apple” + “apple” + “pen” 或者 “pen” + “apple” + “apple” ，强调物品顺序。

• 外for循环遍历物品，内层for循环遍历背包，计算的是组合数——518题、494题
• 外for循环遍历背包，内层for循环遍历物品，计算的是排列数——377题、70题、本题
• 纯完全背包问题，先遍历物品或者先遍历背包，内循环正序遍历，计算的是最小数——322题、279题

5. 举例推导dp数组
   输入: s = “leetcode”, wordDict = [“leet”, “code”]为例
   

6. C++实现

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> wordset(wordDict.begin(), wordDict.end());//为了使用find查找函数
        vector<bool> dp(s.size()+1, false);
        dp[0] = true;
        //排列数 先背包 后物品
        for(int i=1;i<=s.size(); i++)
        {
            for(int j=0; j<i; j++)
            {
                string word = s.substr(j, i-j);//substr(起始位置，截取的个数)
                if(wordset.find(word) != wordset.end() && dp[j]) dp[i] = true;
            }
        }       
        return dp[s.size()];
    }
};

多重背包

多重背包的物品数量是有限个的，完全背包的物品数量是无限的，01背包的物品数量只有一个

有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用，每件耗费的空间是Ci ，价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量，且价值总和最大。

每件物品最多有Mi件可用，把Mi件摊开，就是01背包问题

实现方式1

把物品展开

void test_multi_pack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    vector<int> nums = {2, 3, 2};
    int bagWeight = 10;
    for (int i = 0; i < nums.size(); i++) {
        while (nums[i] > 1) { // nums[i]保留到1，把其他物品都展开
            weight.push_back(weight[i]);
            value.push_back(value[i]);
            nums[i]--;
        }
    }

    vector<int> dp(bagWeight + 1, 0);
    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
        }
        for (int j = 0; j <= bagWeight; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
    }
    cout << dp[bagWeight] << endl;

}
int main() {
    test_multi_pack();
}

实现方式2

把每种商品遍历的个数放在01背包里面在遍历一遍

void test_multi_pack() {
    vector<int> weight = {1, 3, 4};
    vector<int> value = {15, 20, 30};
    vector<int> nums = {2, 3, 2};
    int bagWeight = 10;
    vector<int> dp(bagWeight + 1, 0);


    for(int i = 0; i < weight.size(); i++) { // 遍历物品
        for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
            // 以上为01背包，然后加一个遍历个数
            for (int k = 1; k <= nums[i] && (j - k * weight[i]) >= 0; k++) { // 遍历个数
                dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);
            }
        }
        // 打印一下dp数组
        for (int j = 0; j <= bagWeight; j++) {
            cout << dp[j] << " ";
        }
        cout << endl;
    }
    cout << dp[bagWeight] << endl;
}
int main() {
    test_multi_pack();
}

背包问题总结

背包递推公式

1. 问能否能装满背包（或者最多装多少）：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
   对应题目：416.分割等和子集、1049.最后一块石头的重量 II

2. 问装满背包有几种方法：dp[j] += dp[j - nums[i]];
   对应题目：494.目标和、518. 零钱兑换 II、377.组合总和Ⅳ、70. 爬楼梯进阶版（完全背包）

3. 问背包装满最大价值：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
   对应题目：474.一和零

4. 问装满背包所有物品的最小个数：dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
   对应题目：322.零钱兑换、279.完全平方数

背包遍历顺序

1. 01背包

• 二维dp数组，先遍历物品或者先遍历背包都可以，且第二层for循环是从小到大遍历。
• 一维dp数组，只能先遍历物品再遍历背包容量，且第二层for循环是从大到小遍历。

2. 完全背包

• 一维dp数组，纯完全背包，先遍历物品或者先遍历背包都可以，且第二层for循环是从小到大遍历。
• 求组合数，外层for循环遍历物品，内层for循环遍历背包，518.零钱兑换II、494题
• 求排列数，外层for循环遍历背包，内层for循环遍历物品，377. 组合总和 Ⅳ、70. 爬楼梯进阶版（完全背包）、139. 单词拆分
• 求最小数，先遍历物品或者先遍历背包都可以，322. 零钱兑换、279.完全平方数