YOLO(你只需看一眼)技术通讲(基于论文与开源代码)
YOLO通讲
- 前言
- YOLO v1
-
- 论文及项目地址
- 介绍
- 模型架构
-
- 统一检测
-
- 边界框的置信度
- 类置信度
- 网络设计
- 训练
- 模型局限
- 总结
- YOLO v2
-
- 模型改进
-
- 正则化批处理
- 使用高分辨率分类器
- 卷积化锚盒
- 维度聚类
前言
YOLO作为现在目标检测技术中较为基础且流行的技术之一。本文将以开源者的论文与模型为基础讲述YOLO技术的v1至v8的技术原理与实现。该篇可以作为是YOLO系列论文导读或是重要知识的简介,当然对于v5及之后基于模型的优化更迭,我们将从模型出发进行分析学习。
YOLO v1
论文及项目地址
Yolo v1 论文地址
Yolo v1 项目地址
介绍
You Only Look Once即我们常说的YOLO。对于YOLO技术的第一版,我认为讲其摘要部分全部放在这里都不为过:
We present YOLO, a new approach to object detection. Prior work on object detection repurposes classifiers to perform detection. Instead, we frame object detection as a regression problem to spatially separated bounding boxes and associated class probabilities. A single neural network predicts bounding boxes and class probabilities directly from full images in one evaluation. Since the whole detection pipeline is a single network, it can be optimized end-to-end directly on detection performance. Our unified architecture is extremely fast. Our base YOLO model processes images in real-time at 45 frames per second. A smaller version of the network, Fast YOLO, processes an astounding 155 frames per second while still achieving double the mAP of other real-time detectors. Compared to state-of-the-art detection systems, YOLO makes more localization errors but is less likely to predict false positives on background. Finally, YOLO learns very general representations of objects. It outperforms other detection methods, including DPM and R-CNN, when generalizing from natural images to other domains like artwork.
这里开篇指出YOLO技术与传统目标检测算法的不同,从一开始的单个图片的学习识别,到使用滑动窗口进行卷积神经网络学习。YOLO的创新点在于:从原来固定的、人为设置的图形检测窗口,设计为或者说是训练为一种自适应的图形检测窗口。
Instead, we frame object detection as a regression problem to spatially separated bounding boxes and associated class probabilities.
因此,YOLO将会使用一个神经网络去预测出检测边界窗(bounding box)与物体类别。
Introduction部分,大致讲述之前的检测模型(滑动窗口)的复杂与自己(YOLO)的简单。另外,叫YOLO(you only look once)指的是可以像人类一样只看一眼就识别出图像及种类。这里这个命名应该就是用来对比滑动窗口需要不断的更新检测边界框进行检测的过程。这一部分论文介绍了YOLO对比其他现有目标检测算法的三点优势:
- YOLO非常快(对比滑动窗口)
- YOLO可以全局预测(对比滑动窗口与区域推荐R-CNN)
- YOLO可以泛化表示学习对象(对比DPM与R-CNN)
这里可能需要解释一下第二点和第三点,第二点因为YOLO需要对边界框进行预测所以并不是单例的区域进行独立的学习,这里是有利于不同区域间的关联建立的。第三点是论文认为YOLO具有更高的泛化能力在面对其他问题或是异常输入的情况下不容易崩溃这一点我们需要在后面通过模型的架构与式子来理解。
当然,论文提出相较于当时最为顶尖的目标检测技术YOLO v1在检测的精准度上尚有不及,但是检测的速度快。
模型架构
统一检测
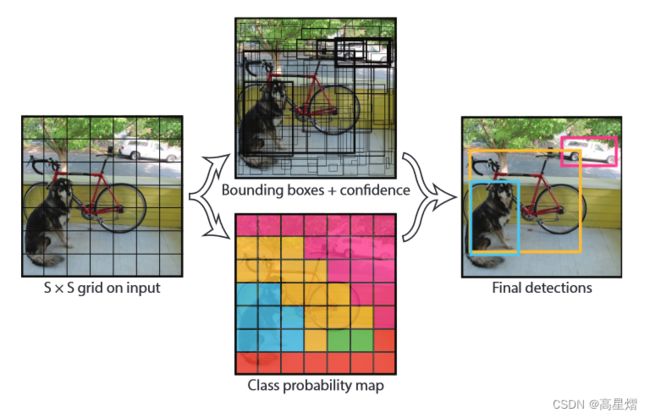
首先,将输入图像划分为S*S个的网格。如果一个物体的中心点落在一个网格单元中,则这个网格单元就用来负责检测这个物体。
每个网格单元都要预测出B个检测边界框(bounding box)以及对于这些边界框的置信度(可信度);并且,每一个网格单元要预测一组待分类的类别条件概率集合。注意这里每个网格单元只预测一组类别的条件概率而非每个bounding box都预测一组。
边界框的置信度
每个网格预测出b个边界框以及对这些边界框的自信程度,即自信分数与预测框与真实框的交并比的乘积,记为confidence,表示为:
C o n f i d e n c e = P r ( O b j e c t ) × I O U p r e d t r u t h Confidence = Pr(Object)\times IOU_{pred}^{truth} Confidence=Pr(Object)×IOUpredtruth
文至此处出现了第一个式子,批注一点,对于论文中的每个式子,本文均会去进行分析与推导,所以don’t worry about them
这里Pr(Object)即是自信分数,模型对每一预测出的bounding box包含物体的可能性概率,而后面的预测框与真实框的交并比是用来约束预测框的精准度,提升bounding box对物体的“描边度”。试想在对模型进行严苛的bounding box精准预测训练后,如果没有交并比的加入,模型反馈出的bounding box将是一个包含了物体的全部但是及其大的一个bounding box,甚至是整个输入图像。
类置信度
上述提及每个网络单元既要预测出b个bounding box以及每个bounding box的置信度,还要预测出对于每个类的条件概率。
C o n d i t i o n a l _ C l a s s _ P r o b a b i l i t i e s = P r ( C l a s s i ∣ O b j e c t ) Conditional\_ Class\_ Probabilities = Pr(Class_i|Object) Conditional_Class_Probabilities=Pr(Classi∣Object)
这里使用条件概率原因在于我们无法百分百的确认检测物体成立,所以这个类别的概率是要建立在对于物体检测的置信度上。
在上述我们计算了边界框的置信度以及检测类别的条件概率集合,我们可以将类别条件概率集与边界框的置信度相乘,就得到了一个网格单元预测出不同的检测边界框对于类别的预测值,论文中将其称作对于每一边界框的特定类的置信分数,如下:
P r ( C l a s s i ∣ O b j e c t ) × ( P r ( O b j e c t ) × I O U p r e d t r u t h ) = P r ( C l a s s i ) × I O U p r e d t r u t h Pr(Class_i|Object)\times (Pr(Object)\times IOU_{pred}^{truth}) = Pr(Class_i)\times IOU_{pred}^{truth} Pr(Classi∣Object)×(Pr(Object)×IOUpredtruth)=Pr(Classi)×IOUpredtruth
这个分数很好的将该特定类别出现在检测框中的概率与预测出的检测框的拟合度想结合。
所以在编码的时候我们将要包含这两个参数,也就是一个S * S * (B * 5 + C)规模的张量的由来。每一个网格单元需要预测出B个bounding box,一个bounding box用一个四元组来表示(x, y, w, h),即中心点的坐标(x, y),以及框的宽w以及框高h。这些数据要编码起来进行求解bounding box 的交并比,同时还有每个边界框的置信度,这就是B * 5。同样,对于每个边界框我们都要计算其中每个类别的出现概率,假定一共有C个类,故此,对于一个网格单元我们需要编码(B * 5 + C)个数据量。而对于整个输入图像,我们一共有S*S个网格,所以我们的预测将会被编码为一个S * S * (B * 5 + C)的张量。
网络设计
YOLO v1网络设计这块,作者延用了GoogLeNet模型,将其中的inception modules替换成了一个1×1的reduction层,接着一个3×3的卷积层。
可能大家对这个GoogLeNet的Inception module 不太了解,下图是inception module v1:

这里我们可以清晰的看到,inception module v1 是将1x1,3x3,5x5的卷积层和3x3的最大池化层堆叠在一起,从而增加了网络的宽度。这个在极大程度上解决了过往为了训练更大网络结构而进行不断的加深网络层级所产生的梯度消失现象。
关于Inception v1 module
这里YOLO v1的网络层级也可以清晰的看出,卷积层24层,全连接层2层。前面的全连接层用以提取图像中的特征,全连接层用以预测bounding box的坐标与各种概率。
训练
We use the Darknet framework for all training and inference
记住这个Darknet,之后还有一个Darknet的主干网络,这个Darknet在这里应该指的是这个深度学习模型。
由于将卷积层与全连接层加入到预训练模型中可以提升性能。Yolo将4个卷积层以及两个任意初始权重的全连接层加入到了预训练过程中。
在部署好网络层级后,在最终层就可以进行预测坐标以及概率了。先将bounding box宽与高进行正则化,使其取值落在0至1之间;并将其横坐标以及纵坐标依据特定网格单元的偏置量进行参数化,以至于它们的值在0到1之间。
Yolo对最终层使用线性激活函数,对其他所有层使用渗漏整流激活(leaky rectified linear activation)可以说是和渗漏整流单元(Leaky Relu)类似的处理。如下式:
ϕ ( x ) = { x , i f x > 0 0.1 x , o t h e r w i s e \phi(x) =\left\{ \begin{array}{ll} x, \qquad \ \ \ \ \ if\ \ x>0 \\ 0.1x, \qquad otherwise\\ \end{array} \right. ϕ(x)={x, if x>00.1x,otherwise
如图:

这样可以可以有效防止梯度爆炸,并可以由于其在负数域仍然保持斜率,则可以解决一般Relu的负向坏死的问题。
在设计完激活函数后,便要开始着手设计损失函数。一开始论文为了便于求解最优解,便以残差平方和(SSE)作为损失函数,如下:
L o s s = ∑ i = 0 S 2 ∑ c ∈ c l a s s e s [ ( p i ( c ) − p ^ i ( c ) ) 2 ] Loss = \sum\limits_{i=0}^{S^2}\sum\limits_{c\in classes}[(p_i(c)-\hat{p}_i(c))^2] Loss=i=0∑S2c∈classes∑[(pi(c)−p^i(c))2]
但是发现那些不包含物体的网格单元计算出的置信度,会压倒包含检测对象网格单元的梯度。会导致模型不稳定,并且会在早期出现分歧。为了解决这一问题,yolo在损失函数中加入对bounding box的损失。而在计算bounding box的损失值的时候,我们就需要计算出对边框预测的坐标和宽高的残差以及类边框的置信度的损失。如下:
L o s s = ∑ i = 0 S 2 ∑ j = 0 B [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] Loss = \sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(x_i-\hat{x}_i)^2+(y_i-\hat{y}_i)^2] Loss=i=0∑S2j=0∑B[(xi−x^i)2+(yi−y^i)2] + ∑ i = 0 S 2 ∑ j = 0 B [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] +\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(w_i-\hat{w}_i)^2+(h_i-\hat{h}_i)^2] +i=0∑S2j=0∑B[(wi−w^i)2+(hi−h^i)2] + ∑ i = 0 S 2 ∑ j = 0 B [ ( C i − C ^ i ) 2 ] + \sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(C_i-\hat{C}_i)^2] +i=0∑S2j=0∑B[(Ci−C^i)2] + ∑ i = 0 S 2 ∑ c ∈ c l a s s e s [ ( p i ( c ) − p ^ i ( c ) ) 2 ] +\sum\limits_{i=0}^{S^2}\sum\limits_{c\in classes}[(p_i(c)-\hat{p}_i(c))^2] +i=0∑S2c∈classes∑[(pi(c)−p^i(c))2]
但是,在我们需要反映出:较之小bounding box 小误差,大bouding box 小误差更为精准。YOLO v1的方法是将求宽w高h的损失时将w与h用√w与√h替代。

很明显,可以对√x求导,这个函数的增长率随着x的增大而减少,则可以说明,若是关于中心点对称的两点,更大的横轴其函数值与中心点的函数值的差值更小。即,在相同差距下,更加倾向与选择更大的bounding box。

即:
L o s s = ∑ i = 0 S 2 ∑ j = 0 B [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] Loss = \sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(x_i-\hat{x}_i)^2+(y_i-\hat{y}_i)^2] Loss=i=0∑S2j=0∑B[(xi−x^i)2+(yi−y^i)2] + ∑ i = 0 S 2 ∑ j = 0 B [ ( w i − w ^ i ) 2 + ( h i − h ^ i ) 2 ] +\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(\sqrt{w}_i-\sqrt{\hat{w}}_i)^2+(\sqrt{h}_i-\sqrt{\hat{h}}_i)^2] +i=0∑S2j=0∑B[(wi−w^i)2+(hi−h^i)2] + ∑ i = 0 S 2 ∑ j = 0 B [ ( C i − C ^ i ) 2 ] + \sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}[(C_i-\hat{C}_i)^2] +i=0∑S2j=0∑B[(Ci−C^i)2] + ∑ i = 0 S 2 ∑ c ∈ c l a s s e s [ ( p i ( c ) − p ^ i ( c ) ) 2 ] +\sum\limits_{i=0}^{S^2}\sum\limits_{c\in classes}[(p_i(c)-\hat{p}_i(c))^2] +i=0∑S2c∈classes∑[(pi(c)−p^i(c))2]
这样就解决了对bounding box的预测,但是对于未检测物体的网格单元对整个模型稳定性的影响,我们还应该通过设置权值方式防止未检测网格坏死,对模型梯度产生极具影响,则设置一个权值(类似与上面讲过的leaky ReLU),我们将加大对边界框的预测权值,并赋予未检测出类网格单元一个较小的权值以保证活性,令λcoord=5,λnoobj=0.5。则我们的损失函数最终如下:
L o s s = λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B I i j o b j [ ( x i − x ^ i ) 2 + ( y i − y ^ i ) 2 ] Loss =\lambda_{coord}\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}\mathbb{I}_{ij}^{obj} [(x_i-\hat{x}_i)^2+(y_i-\hat{y}_i)^2] Loss=λcoordi=0∑S2j=0∑BIijobj[(xi−x^i)2+(yi−y^i)2]
+ λ c o o r d ∑ i = 0 S 2 ∑ j = 0 B I i j o b j [ ( w i − w ^ i ) 2 + h i − h ^ i ) 2 ] + \lambda_{coord}\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}\mathbb{I}_{ij}^{obj}[(\sqrt{w}_i-\sqrt{\hat{w}}_i)^2+\sqrt{h}_i-\sqrt{\hat{h}}_i)^2] +λcoordi=0∑S2j=0∑BIijobj[(wi−w^i)2+hi−h^i)2] + ∑ i = 0 S 2 ∑ j = 0 B I i j o b j [ ( C i − C ^ i ) 2 ] +\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}\mathbb{I}_{ij}^{obj}[(C_i-\hat{C}_i)^2] +i=0∑S2j=0∑BIijobj[(Ci−C^i)2] + λ n o o b j ∑ i = 0 S 2 ∑ j = 0 B I i j n o o b j [ ( C i − C ^ i ) 2 ] +\lambda_{noobj}\sum\limits_{i=0}^{S^2}\sum\limits_{j=0}^{B}\mathbb{I}_{ij}^{noobj}[(C_i-\hat{C}_i)^2] +λnoobji=0∑S2j=0∑BIijnoobj[(Ci−C^i)2] + ∑ i = 0 S 2 I i o b j ∑ c ∈ c l a s s e s [ ( p i ( c ) − p ^ i ( c ) ) 2 ] +\sum\limits_{i=0}^{S^2}\mathbb{I}_{i}^{obj}\sum\limits_{c\in classes}[(p_i(c)-\hat{p}_i(c))^2] +i=0∑S2Iiobjc∈classes∑[(pi(c)−p^i(c))2]
其中, I i o b j \mathbb{I}_{i}^{obj} Iiobj记作物体是否出现在网格单元i中, I i j o b j \mathbb{I}_{ij}^{obj} Iijobj表示bounding box j是否负责预测该物体。
通过上述机制,我们达成了,只有物体在网格单元内,我们才进行惩罚分类误差;同样,我们只会对负责的预测的bounding box 惩罚其分类误差。
论文中讲述了一个训练的范例,是使用PASCAL VOC检测数据集的,大家可以看看。
模型局限
对于作者在github中创建的Yolo v1模型(见论文及项目地址第二个github链接这些问题为作者一开始项目中存在的,作者已在论文中提出了修改,可见上述)的局限有如下几点:
- Yolo v1模型难以处理较小物体
- 该模型对于处理物体的周边物体数量有特殊限制
- 模型在泛化到其他纵横比的物体预测上效果较差
- 在进行bounding box推测时,使用的特征粗糙
- 没有区分同等误差下较大的bounding box与较小的区别。
前两点产生的原因是因为YOLO对bounding box的预测具有很强的空间限制,当时作者采用的是一个网格单元只预测两个bounding box并只能预测一个类。
三四点是因为,作者在输入图像时采用了多个下采样在模型中,而在训练时是只用这个数据训练的bounding box
最后一点,是因为当时作者并没有考虑到对于较大bounding box的小误差与较小bounding box的小误差的处理上应该采用不同的权值。前者对模型的影响通常是良好的,后者则是对计算置信度时的交并比有着很大影响。
总结
我认为YOLO v1的主要原理已经全部讲述了,而论文的后面部分讲述了:Yolo v1与其他模型的在一些方面上的比较,以及将其运用到范例上的实验结果以及可行性分析。
YOLO v2
上述Yolo v1模型的最后,作者提出了该模型的几点局限,Yolo v2版本则是基于这几点的改进。
模型改进
作者主要针对之前问题提出了4点改进:
- 正则化批处理
- 使用高分辨率分类器
- 卷积化锚盒
- 维度聚类
- 直接位置预测
- 细粒度特征
- 多尺度训练
下文将分别对这几项改进进行详细的叙述:
正则化批处理
使用批处理正则化可以有效的提升模型的收敛性,并且可以避免使用其他形式的正则化需要。 这里的这个原理有在这篇论文中有过提出的,大家可以去参考一二。
S. Ioffe and C. Szegedy. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv preprint arXiv:1502.03167, 2015. 2, 5
YOLO在卷积层中引入了正则化批处理后,在目标检测的mAP上取得了2%的提升。并且,这种方法可以不用再使用dropout来处理过拟合问题了。
使用高分辨率分类器
YOLO将原来的224×224的输入规模改成了448×448的输入图像的规模,这样拥有更大的输入图像分辨率意味着网络在切换学习检测目标的同时,要去适应新的输入分辨率。
对于Yolo v2而言,
- 先在ImageNet上微调了10epochs的全448×448像素分类网络。这样将会给网络时间去调节它的过滤器,以更好的去处理更高的分辨率输入。
- 然后,再在检测时微调结果网络。
这样运用了高分辨率的分辨网络将会给整个模型的mAp提供4%的提升。
卷积化锚盒
YOLO预测bounding box 的坐标是直接在卷积特征提取器的顶端使用全连接层,而不是直接使用faster R-CNN的精选先验框来预测bounding box的坐标。使用只有卷积层的区域最优网络(region proposal network)预测锚盒的偏置量以及置信度。由于预测层是卷积化的,所以这个RPN预测的是特征图中的每个位置的偏移量。预测偏移量而不是坐标,这样可以简化问题,并且可以让网络更容易的去学习。
在Yolo v2中,它移除了全连接层,使用锚盒来预测bounding box。
- 首先先消除一个池化层,使网络的卷积层拥有更高的分辨率输出。
- 缩减网络的图像输入,从448×448缩减到416,这里使用奇数是为了在特征图中只有一个中心点。而yolo的卷积层的32倍的下采样,所以416的输入图像将会得到13×13的输出特征图。
- 再移动锚盒时,需要从空间位置中分离出类预测机,使用每个锚盒的类预测和对象预测来替代。(这里的对象预测是预测推荐bounding box与真实区域的交并比,类预测是用来预测给定包含一个物体的类的条件概率)
在这里使用锚盒会很小的降低模型的精确度,但是召回率得到了较高的提升。
在使用锚盒的时候,会有两个问题:其一是这些锚盒的维度是手工筛选的;其二是模型的不稳定。下面的将会提出解决这些问题的方法。
