2022电工杯数学建模B题解题思路(5G 网络环境下应急物资配送问题)
一、前言
本文是对2022年第十四届 “电工杯” 高校数学建模挑战赛B题:5G 网络环境下应急物资配送问题的解题思路,希望能够对正在学习数学建模或者研究该类问题的读者提供帮助。作者在当届的比赛中,获得了本科组三等奖的成绩,并且在这个的基础上进行了后期的思路改进,可以说这个思路还是具有一定的合理性的。
PS:当年的获奖证书到现在没发,不知道组委会在搞什么飞机。
喊话组委会:大哥们,23年的都快出成绩了,你们搞啥呢?
二、问题背景
三、具体问题
四、假设补充
五、解题思路
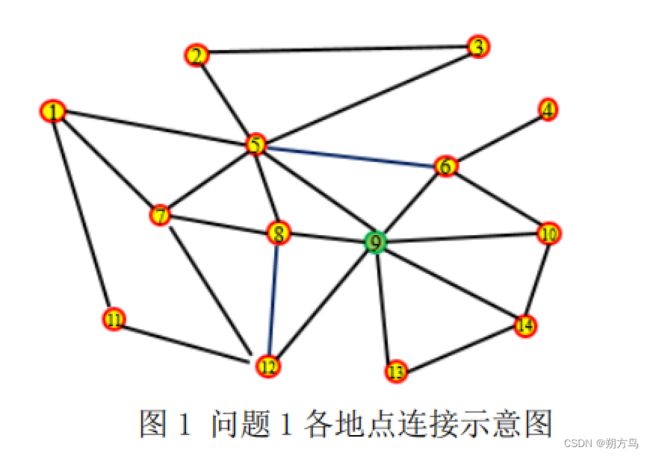
问题 1:可以采用贪心算法来解决。首先在初始状态下,选定出发点为第 9 个地点,并将所有应急物资集中在该点。然后按照图 1 的路线情况,从该点出发依次经过可达的未访问过的点,当载重达到 1000 千克时,返回第 9 个地点重新装载物资,并再次出发进行下一轮配送。重复该过程,直到所有点均被访问并完成一次整体配送。在此过程中,记录下各点访问次序以及每个配送轮次的时间消耗,最终得出完成一次整体配送的最优方案。
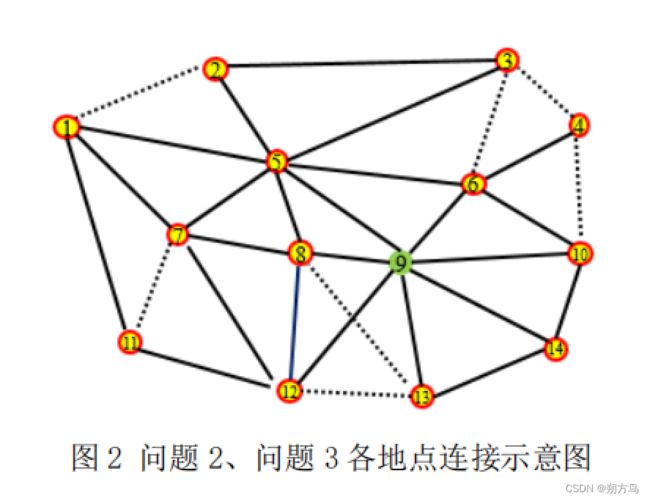
问题 2 和 3:可以采用分支限界算法寻找最优解。首先设定状态空间树的根节点为出发点为第 9 个地点,由此展开子节点,对每一个节点进行处理,计算出在该节点时所有未访问过的点,满足载重不超过配送车辆最大载重的情况下,所能到达的最远距离。采用优先队列对子节点进行排序,得到当前最优解。以此方式层层展开子节点,直到得到整体配送的最优解。
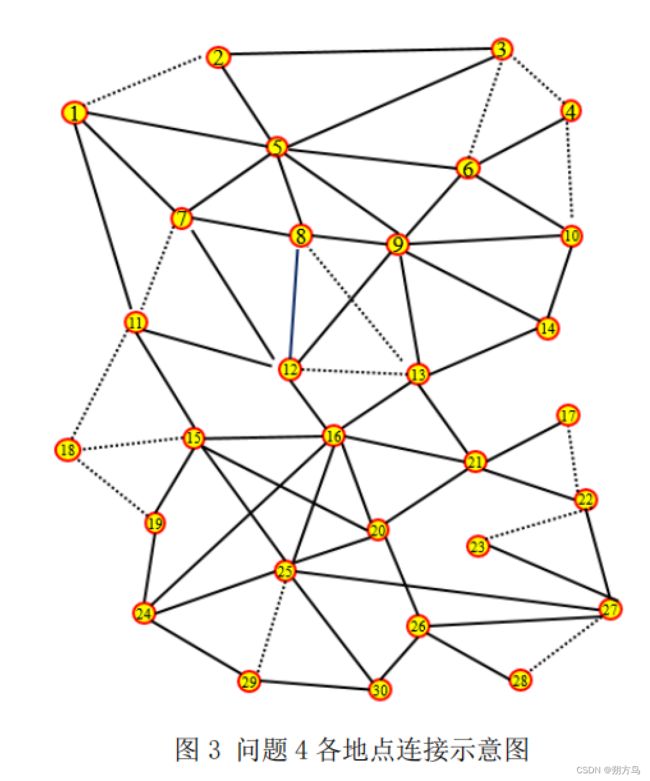
问题 4:也可以采用分支限界算法。首先设定状态空间树的根节点是两个应急物资集中地点任意选定一点。然后在状态空间树中依次展开子节点,对于每一个未访问过的点,先计算它与已选定的地点之间的距离,若距离都小于或等于配送车辆最大载重,就将其加入已访问的点的集合中,并计算出它们可以到达的最远距离。将这些点作为状态空间树中的子节点,以相同方式进行处理,直到经过所有点且回到已选定地点,得出整体配送的最优方案以及最佳位置。
六、附上几个典型代码
这里是几个符合该问题背景的典型算法代码:
(一)贪心算法
以问题一为例:
```
def greedy_algorithm(graph):
n = len(graph)
visited = set()
max_load = 1000 # 配送车辆最大载重
current = 8 # 初始状态下出发点为第9个地点
visited.add(current)
seq = [current]
load = 0
time = 0
while len(visited) < n:
next_node = -1
max_distance = 0
# 遍历未访问的所有点,选择距离当前点最远的可达点
for i in range(n):
if i not in visited and graph[current][i] > 0 and graph[current][i] + graph[i][8] <= max_load - load:
if graph[current][i] > max_distance:
max_distance = graph[current][i]
next_node = i
# 若没有可达点,则返回起始点重新装载物资
if next_node == -1:
load = 0
time += graph[current][8]
current = 8
seq.append(current)
else:
visited.add(next_node)
seq.append(next_node)
load += graph[current][next_node]
time += graph[current][next_node]
current = next_node
# 返回访问顺序和总时间
return seq, time
```其中,变量 `graph` 表示图的邻接矩阵,`n` 表示总的点数,`visited` 保存已经访问过的点编号,`max_load` 表示配送车辆的最大载重量,`current` 表示当前所在点,`seq` 保存点的访问顺序,`load` 保存当前载重,`time` 保存完成一次整体配送的总时间。函数返回点的访问顺序和总时间。
(二)问题二的分支限界算法的典型代码
以下是问题二的分支限界算法的典型代码实现:
```
import heapq
def branch_and_bound(graph, max_load):
n = len(graph)
visited = set()
root = 8 # 初始状态下出发点为第9个地点
# 初始化状态空间树的根节点
heap = [(0, root, frozenset([root]), 0)]
best_seq = None
best_time = float('inf')
while heap:
_, current, visited_set, time = heapq.heappop(heap)
# 判断该节点是否需要展开子节点
if len(visited_set) == n:
if time < best_time:
best_time = time
best_seq = tuple(visited_set)
else:
# 找到所有可达的未访问过的节点
new_nodes = []
for i in range(n):
if i not in visited_set and graph[current][i] > 0:
if graph[current][i] + graph[i][8] <= max_load:
new_nodes.append(i)
else:
distance = graph[current][i] + graph[i][8] - max_load
h = distance / 5 # 假设无人机速度为5m/s
new_nodes.append((i, h))
# 对可行节点和无人机情况进行排序
new_nodes = sorted(new_nodes, key=lambda x: x[1] if isinstance(x, tuple) else 0)
# 展开子节点,并加入优先队列中
for node in new_nodes:
if isinstance(node, tuple):
i = node[0]
h = node[1]
new_visited_set = visited_set | frozenset([i])
new_time = time + h
heapq.heappush(heap, (new_time, i, new_visited_set, time))
else:
i = node
new_visited_set = visited_set | frozenset([i])
new_time = time + graph[current][i]
heapq.heappush(heap, (new_time, i, new_visited_set, new_time))
# 将节点编号转换为点的访问顺序
best_seq = [i for i in best_seq]
best_seq.remove(root)
best_seq.insert(0, root)
# 返回点的访问顺序和总时间
return best_seq, best_time
```其中,变量 `graph` 表示图的邻接矩阵,`max_load` 表示配送车辆的最大载重量,`n` 表示总的点数,`visited_set` 保存已经访问过的点编号的集合,`root` 表示初始状态下出发点为第 9 个地点,`heap` 是优先队列,用于保存待展开的子节点。函数返回点的访问顺序和总时间。
七、总结
本次解题思路的主要内容是基于应急物资的配送问题,涉及到贪心算法和分支限界算法的应用。对于问题一,采用贪心算法求解,依次遍历未访问的所有点,选择距离当前点最远的可达点,实现较为简单;对于问题二和问题三,采用分支限界算法求解,以图的状态空间树表示所有可能的配送方案,以找到最优解为目标,算法思路更加复杂;对于问题四,同样采用分支限界算法求解,将配送车辆最大载重量设为 500 千克,同时需要计算两个应急物资集中地点的最佳位置,思路相对于问题二和三更加复杂。总体来说,以上解题思路需要结合具体问题,分析问题背景,给出合适的模型和算法,找到最优配送方案。