【NLP】从双曲面到双曲几何庞加莱盘
一、说明
在研究双曲空间的时候,不能不遇到双曲面的问题。双曲几何在什么样的双曲面建立?其它几何元素在双曲面的表现。庞加莱盘不是双曲几何的一部分,而是一个投影平面,自然语言处理中,图网络不是卷积神经网络。本篇从双曲方程开始,展开双曲空间的探讨。
二、双曲面总论
2.1 特征和属性
双曲面是一种曲面,其定义为与一个双曲面生成元 H(平面曲线)相交的所有切面均为双曲线。双曲面具有以下性质:
-
双曲面是一个二次曲面,可以用二次方程描述。
-
双曲面可以分为两类:单叶双曲面和双叶双曲面。单叶双曲面只有一个曲面,而双叶双曲面有两个对称的曲面。
-
双曲面的曲率比较复杂,在不同点处的曲率大小和方向都不同。它的曲率中心在参数平面上是一个双重点,对应着双曲线的两个焦点。
-
双曲面的切向量和法向量在不同点处都有不同的方向。在单叶双曲面上,切向量、法向量和曲面上的任意一点的位置向量共面;在双叶双曲面上,切向量、法向量和曲面上的任意一点的位置向量不共面。
-
双曲面具有对称性,其中包括轴对称、中心对称和面对称。这些对称性在解决一些几何问题时非常有用。
-
双曲面是一种非欧几何,与欧几里得几何和椭圆几何不同。因此,它的性质与欧几里得几何和椭圆几何有很大的区别。
2.2 单页曲面
在几何学中,单叶双曲面(有时称为旋转双曲面或圆形双曲面)是通过围绕其主轴旋转双曲线而产生的表面。
1、单叶双曲面方程:
![]()
单叶双曲面包含两根线条旋转的锥面为渐进面,这是一对双重曲面。在a = b的情况下,单叶双曲面是旋转表面,可以通过旋转两条线l+或l-,它们偏向旋转轴。x(t)为:平面部分因为一般双曲面是单叶双曲面,它的结果也适用于一般情况 。
参数方程:
可令:
单叶双曲面方程:可以定义双曲面的笛卡尔坐标,类似于球面坐标,保持方位角θ∈[0,2π),φ是水平旋旋转圆之角度参数。
2.3 双叶曲面
双曲面是二次曲面,其可以被定义为三个变量中的二维多项式的点的集合的表面。 在二次曲面中,双曲面的特征在于不仅具有对称中心,而且让平面和其相交还能形成锥体、柱体等。 双曲面还具有三对垂直对称轴和三对垂直对称平面。
2、双叶双曲面方程:
![]()
参数方程:
可令:
双曲面是可以通过使用方向定标使其变形而从旋转抛物面获得的表面。
2.4 马鞍面
马鞍面是一种更复杂的双曲面形式,目前合适用途似乎不多,但作为系统论述,这里也必须介绍。
方程:
![]()
作图如下:
三、双曲面空间
3.1 距离和测地线
一般地,在欧几里得空间,总是有“两点之间距离直线最短”,这是因为在欧氏几何学中,平面曲率为0的原因。
下面举一个反例:
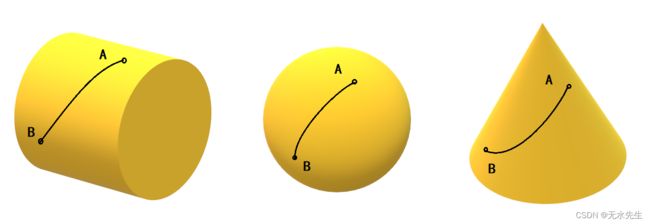
因为两个点A和B不在一个平面上,所以,A和B所连的直线不存在,因此,A和B的最短路程需要按照A和B所在地形具体测量,因而这种受地形影响的最短路径测量线,叫做测地线。更一般地,在光滑曲面上两点的最短路程,就和弯曲面的具体曲率有关,且更抽象不易获得。关于如何获取曲面的测地线,请看文:xxxxxx
定理:曲面上非直线的曲线是测地线的充分必要条件是除了曲率为零的点以外,曲线的主法线重合于曲面的法线。
3.2 双曲空间
双曲面空间和欧几里得空间是两种不同的几何空间。它们之间的主要区别在于:
- 欧几里得的几何始终在平面上进行,平面曲率为0’
- 双曲几何在一只双叶曲线上进行,其曲率为-1。
- 双曲几何继承欧几里得的前四个公理。
- 双曲几何的第五公理是:过一条直线外一个点,可以做出无数条平行线。
- 在双曲面空间中,直线不存在,而是由一些曲线来代替。
曲线在空间中弯曲得越来越多,但永远不会相交。
相比之下,欧几里得空间是一种平坦的几何空间,其曲率为零。在欧几里得空间中,直线是直的,两点之间的最短路径也是一条直线。欧几里得空间可以看作是一个无限大的平面,其中所有的点与直线都处于同一平面上。
四、庞加莱盘
定义:庞加莱盘(Poincaré disk)是由法国数学家亨利·庞加莱于19世纪末发明的,主要用于研究非欧几何学中的几何形态和变换。这个盘是一个以单位圆为界限的上半平面模型,可以将平面中的所有点映射到圆盘内。在庞加莱盘上,两个向量的内积等于它们在欧几里得平面上的内积除以一个常数因子。
庞加莱圆盘模型,和克莱因模型一样,都与双曲面模型射影相关。如果我们有双曲面模型中双曲面的上叶中一点 [t, x1, ..., xn],这样就定义了双曲面模型中一点,我们可以通过与 [-1, 0, ..., 0] 连接一条直线将其投影到超曲面 t = 0 上,所得是庞加莱圆盘模型中的对应点。
五、知识图谱和word-Net
5.1 知识图谱
知识图谱是一种以图形化的方式表示知识领域中实体、属性和它们之间关系的方法,通过对实体和关系的抽象和建模,使得计算机能够更好地理解并处理自然语言的语义。知识图谱主要包括三部分:实体、属性和关系。实体是指具体的事物、概念或事件,属性是指实体的特征或描述,关系是指实体之间的相互联系。知识图谱是当前人工智能和自然语言处理领域的热门研究方向,应用于搜索引擎、智能问答、语义分析等领域。
5.2 word-Net
WordNet 是一个英语词汇数据库,它将单词分组为称为同义词集的同义词集,提供简短、通用的定义,并记录同义词集之间的各种语义关系。它是由认知心理学家乔治·A·米勒 (George A. Miller) 和他在普林斯顿大学的团队创建的。 WordNet 可用于自然语言处理应用,例如文本分类、信息检索和机器翻译。
密切注意:这里的网络是图神经网络,不是卷积神经网络。不要混淆。
5.3 庞加莱映射的好处
- 旁及来映射,将欧氏数据映射到双曲空间,避免了数据稀疏性。
- 庞加莱映射具有层次性,一般深度神经网络是平坦的。因此图形网络更合适。
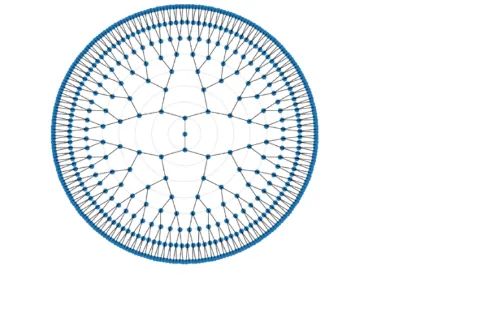
- 而双曲空间volume呈指数级增长,恰好与现实网络的tree-like特性相匹配。
六、部分程序代码
6.1 单页双曲
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
# ax = fig.gca(projection='3d')
ax = fig.add_axes(Axes3D(fig))
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
Z1 = np.sqrt( 4.*(X**2 + Y**2)/1. - 1)
Z2 = -np.sqrt( 4.*(X**2 + Y**2)/1. - 1)
xcolors = X - min(X.flat)
xcolors = xcolors/max(xcolors.flat)
surf1 = ax.plot_surface(X, Y, Z1, rstride=1, cstride=1, facecolors=cm.hot(xcolors),
linewidth=1)
surf2 = ax.plot_surface(X, Y, Z2, rstride=1, cstride=1, facecolors=cm.hot(xcolors),
linewidth=1)
plt.show()
6.2 双叶双曲面
首先从python做出双曲面,在三维空间观察之。
from matplotlib import cm
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
# ax = fig.gca(projection='3d')
ax = fig.add_axes(Axes3D(fig))
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
Z1 = np.sqrt(4.*(X**2 + Y**2)/1. + 1)
Z2 = -np.sqrt(4.*(X**2 + Y**2)/1. + 1)
xcolors = X - min(X.flat)
xcolors = xcolors/max(xcolors.flat)
surf1 = ax.plot_surface(X, Y, Z1, rstride=1, cstride=1, facecolors=cm.hot(xcolors),
linewidth=1)
surf2 = ax.plot_surface(X, Y, Z2, rstride=1, cstride=1, facecolors=cm.hot(xcolors),
linewidth=1)
plt.show()结果图:
6.3 马鞍面
from numpy import *
from matplotlib.pyplot import *
from mpl_toolkits.mplot3d import Axes3D
x = linspace(-2, 2, 100)
y = linspace(-2, 2, 100)
X, Y = meshgrid(x, y)
Z = X**2 - Y**2
fig = figure()
# ax = axes(projection='3d')
ax = fig.add_axes(Axes3D(fig))
ax.plot_surface(X, Y, Z, color='b')
show()