FWI 地震数据的认识
目录
1、数据来源。
1)SEG 系列。
2)OpenFWI 系列。
2、数据量,尺寸。
1) SEG 包含两个数据集:SEGSaltData 和 SimulateData。
2)OpenFWI 包含12个数据集:
3、地震数据对应的观测系统。
1) SEG系列
2)OpenFWI系列
4、显示数据的源码
5、正演的原理及源码
6、我的疑问:
地震数据是非常宝贵的资源,很多真实数据并不是公开的,目前在网上流传的都是合成数据。我将从以下角度来介绍合成数据:
1、数据来源。
1)SEG 系列。
数据源自论文: Yang F, Ma J. Deep-learning inversion: A next-generation seismic velocity model building method DL for velocity model building[J]. Geophysics, 2019, 84(4): R583-R599.
作者基于unet架构,实现了端到端的全波形反演,从地震数据直接获得速度模型,并在盐体数据上测试性能。
论文代码:GitHub - YangFangShu/FCNVMB-Deep-learning-based-seismic-velocity-model-building: Deep-learning inversion: A next-generation seismic velocity model building method
2)OpenFWI 系列。
数据源自论文:Deng C, Feng S, Wang H, et al. OpenFWI: Large-scale Multi-structural Benchmark Datasets for Full Waveform Inversion[J]. Advances in Neural Information Processing Systems, 2022, 35: 6007-6020.
数据和代码网址: https://openfwi-lanl.github.io/
它涵盖了地球物理的多个领域(界面、断层、CO2储层等),涵盖了不同的地质地下构造(平面、曲线等),包含了不同数量的数据样本(2K - 67K),还包括3D FWI数据集。此外,比较了三种二维FWI方法:InversionNet[20]提出了一种全卷积网络来模拟地震反演过程;VelocityGAN[27]采用基于gan的模型求解FWI;UPFWI[31]将正演建模与CNN连接在一个回路中,实现无监督学习,无需地面真值速度图进行训练。还有一种三维FWI方法:InversionNet3D[30]将InversionNet扩展到三维领域。为了减少内存占用和提高计算效率(即3D反演中最具挑战性的两个障碍),该网络在编码器中使用了群卷积,并通过基于加性耦合的可逆层采用了部分可逆架构[46]。
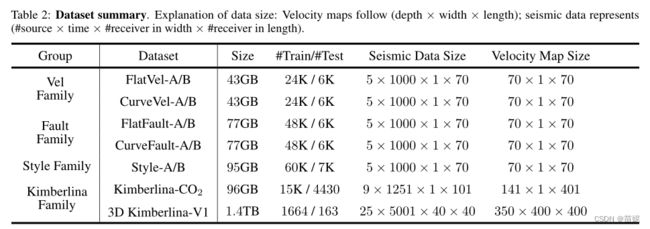
2、数据量,尺寸。
1) SEG 包含两个数据集:SEGSaltData 和 SimulateData。
| 数据集 | SEGSaltData | SimulateData |
| 数量(train+test) | 140(130+10) | 1700(1600+100) |
| 地震数据尺寸 | 400 x 301 | 201 x 301 |
| 速度模型尺寸 | 400 x 301 | 201 x 301 |
2)OpenFWI 包含12个数据集:
其中第二行的 B系列,比第一行的A系列有更高的难度。从左到右,依次为平面(FlatVel-A、FlatVel-B)、曲面(CurveVel-A 、CurveVel-B)、平面断层(FlatFault-A、 FlatFault-B)、曲面断层(CurveFault-A、CurveFault-B)、复杂的野外合成数据(Style-A、Style-B)、二氧化碳储层(Kimberlina-CO2)、三维地震数据(3D Kimberlina-V1)。
在这里要注意,理解下表的尺寸时,如速度模型70x1x70, 中间为1表明是个二维速度模型。
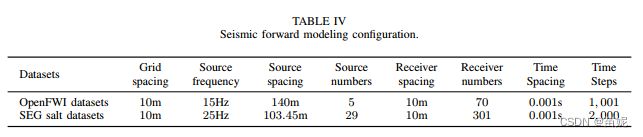
3、地震数据对应的观测系统。
1) SEG系列
参考星移论文
2)OpenFWI系列
4、显示数据的源码
我的数据都存在.mat文件中:
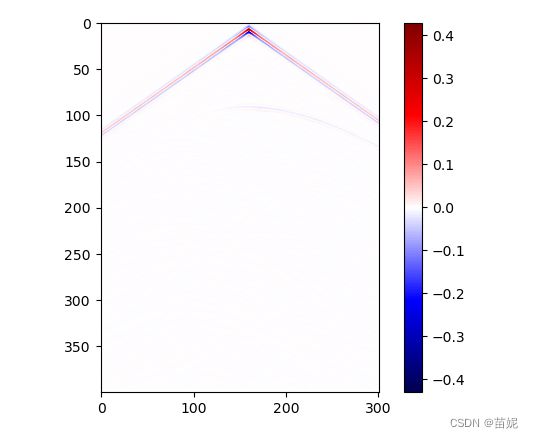
1)显示地震地震数据:
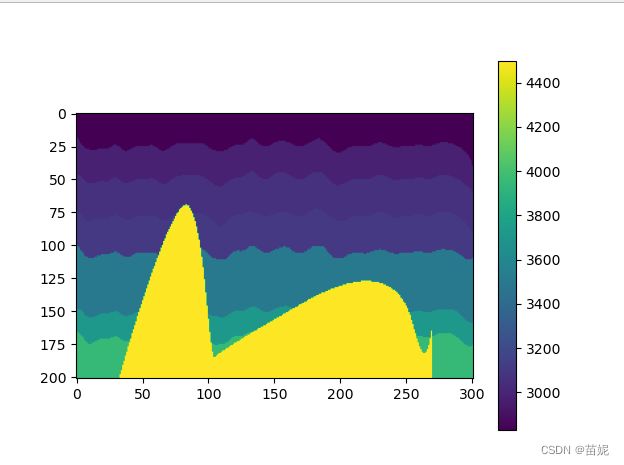
2)显示速度模型:
5、正演的原理及源码
原理及波动方程公式后续补上。
% 对文件夹内所有文件进行计算并存储
% function [] = forward(vdir,vname,gdir,gname,start_num,end_num)
% for i = start_num:end_num
% vfile = [vdir,'/',vname,num2str(i),'.mat']
% gfile = [gdir,'/',gname,num2str(i),'.mat']
% calc(vfile,gfile);
% end
% end
% 对单个速度模型文件计算多炮数据
function [] = forward(vfile,outfile,sn) %sn 炮数
load(vfile,'vmodel'); %加载vfile文件中的vmodel变量
[nz,nx] = size(vmodel);% 201*301
Rec = ones(400,nx,sn);% 400*301 是地震数据的尺寸
%tic用来保存当前时间,而后使用toc来记录程序完成时间,两者往往结合使用
tic;
for i = 1:sn
sx = i*fix(nx/sn); % 这一步的意思是放炮的位置是均匀放置的么?
singleRec = calc(vmodel, sx);
Rec(:,:,i) = singleRec;
end
toc;
save(outfile,'Rec');
end
% 对单炮速度模型进行计算
function singleRec = calc(vmodel, sx)
[nz,nx] = size(vmodel); % x方向网格数(从左到右 和 z方向网格数(从上到下) 201*301
npmlz = 10; % 顶部和底部的PML层厚度
npmlx = 10; % 左边和右边的PML层厚度
% sx = 100; % 震源的x方向网格数
sz = 0; % 震源的z方向网格数 表明震源在地表
dx = 10; % x方向的网格大小 单位:米
dz = 10; % y方向的网格大小 单位:米
nt = 2000; % 计算的总时间步数 在方程的最后下采样5,最后求的400 对应301*400的地震数据尺寸
dt = 1e-3; % 单位时间步长度 单位:秒
ampl = 1.0e0; % 震源子波的震幅
xrcvr = 1:1:nx; % 地面上x方向的接收器位置
nodr = 3; % half of the order number for spatial difference.
B = [1 zeros(1,nodr - 1)]';
A = NaN*ones(nodr,nodr);
for i = 1:1:nodr
A(i,:) = (1:2:2*nodr - 1).^(2*i - 1);
end
C = A\B;
Nz = nz + 2*npmlz;
Nx = nx + 2*npmlx;
rho = 1000*ones(Nz,Nx); % 密度; Unit: kg/m^3. 密度对结果有什么影响? 此处密度1000
rho(fix(Nz/3):end,fix(Nx/2):end) = 500; % 通过修改密度,可以模拟介质中存在不同的物理特性,如不均匀的岩层、气体或液体的存在等
vp = padarray(vmodel,[10,10],'replicate','both'); % 扩展边界
% 边界扩展是为了处理波场模拟中的边界效应,确保在模拟过程中声波传播不会超出vmodel的范围。
% 通过在vmodel的周围添加额外的边界值,可以避免波场反射和干扰。padarray函数的'replicate'选项表示将vmodel的边界值复制并填充到扩展后的边界上。
f0 = 25; % 震源频率 单位 Hz
t0 = 1/f0; % the time shift of source Ricker wavelet; Unit: s; Suggest: 0.02 if fm = 50, or 0.05 if fm = 20.
t = dt*(1:1:nt);
src = (1 - 2*(pi*f0.*(t - t0)).^2).*exp( - (pi*f0*(t - t0)).^2); % the time series of source wavelet. 雷克子波
% The source wavelet formula refers to the equations (18) of Collino and Tsogka, 2001.
%% Perfectly matched layer absorbing factor PML层吸收因子设置
dpml0z = 3*max(vp(:))/dz*(8/15 - 3/100*npmlz + 1/1500*npmlz^2);
dpmlz = zeros(Nz,Nx);
dpmlz(1:npmlz,:) = (dpml0z*((npmlz: - 1:1)./npmlz).^2)'*ones(1,Nx);
dpmlz(npmlz + nz + 1:Nz,:) = dpmlz(npmlz: - 1:1,:);
dpml0x = 3*max(vp(:))/dx*(8/15 - 3/100*npmlx + 1/1500*npmlx^2);
dpmlx = zeros(Nz,Nx);
dpmlx(:,1:npmlx) = ones(Nz,1)*(dpml0x*((npmlx: - 1:1)./npmlx).^2);
dpmlx(:,npmlx + nx + 1:Nx) = dpmlx(:,npmlx: - 1:1);
% The PML formula refers to the equations (2) and (3) of Marcinkovich and Olsen, 2003.
%% Wavefield calculating 依据广义胡克定律求的弹性系数
% rho1 和 rho2 是密度(rho)的副本。它们用于计算波场的系数,与波场更新方程中的密度项有关。
% Coeffi1 和 Coeffi2 是沿 x 轴和 z 轴方向的PML吸收因子的系数。它们根据PML吸收因子(dpmlx 和 dpmlz)和时间步长(dt)计算得出。这些系数在波场更新方程中用于考虑PML的吸收效果。
% Coeffi3 和 Coeffi4 是与密度(rho)和空间步长(dx 和 dz)相关的系数,用于考虑波场更新方程中的空间导数项。
% Coeffi5 和 Coeffi6 是与密度(rho)和速度(vp)的平方以及空间步长(dx 和 dz)相关的系数,用于考虑波场更新方程中的速度和应力项。
% 这些系数是根据弹性介质的性质和PML吸收层的影响,结合波场更新方程中的相关项,计算得出的。它们的计算方式是基于广义胡克定律和对介质参数的离散化模拟。
% 通过使用这些系数,可以准确地更新波场的值,模拟弹性波在介质中的传播和衰减行为。
rho1 = rho; % or = [(rho(:,1:end - 1) + rho(:,2:end))./2 (2*rho(:,end) - rho(:,end - 1))];
rho2 = rho; % or = [(rho(1:end - 1,:) + rho(2:end,:))./2; (2*rho(end,:) - rho(end - 1,:))];
Coeffi1 = (2 - dt.*dpmlx)./(2 + dt.*dpmlx);
Coeffi2 = (2 - dt.*dpmlz)./(2 + dt.*dpmlz);
Coeffi3 = 1./rho1./dx.*(2*dt./(2 + dt.*dpmlx));
Coeffi4 = 1./rho2./dz.*(2*dt./(2 + dt.*dpmlz));
Coeffi5 = rho.*(vp.^2)./dx.*(2*dt./(2 + dt.*dpmlx));
Coeffi6 = rho.*(vp.^2)./dz.*(2*dt./(2 + dt.*dpmlz));
% +++++++++++++++++++++++++++++++++++++ approximate coeffient ++++++++++++++++++++++++++++++++++++++
% Coeffi1 = 1 - dt.*dpmlx;
% Coeffi2 = 1 - dt.*dpmlz;
% Coeffi3 = 1./rho./dx.*dt;
% Coeffi4 = 1./rho./dz.*dt;
% Coeffi5 = rho.*(vp.^2)./dx.*dt;
% Coeffi6 = rho.*(vp.^2)./dz.*dt;
% --------------------------------------------------------------------------------------------------
NZ = Nz + 2*nodr; % All values of the outermost some columns are set to zero to be a boundary condition: all of wavefield values beyond the left and right boundary are null.
NX = Nx + 2*nodr; % All values of the outermost some rows are set to zero to be a boundary condition: all of wavefield values beyond the top and bottom boundary are null.
Znodes = nodr + 1:NZ - nodr;
Xnodes = nodr + 1:NX - nodr;
znodes = nodr + npmlz + 1:nodr + npmlz + nz;
xnodes = nodr + npmlx + 1:nodr + npmlx + nx;
nsrcz = nodr + npmlz + sz;
nsrcx = nodr + npmlx + sx;
Ut = NaN*ones(NZ,NX); % the wavefield value preallocation. 存储波场的值,并在时间步进过程中进行更新
Uz = zeros(NZ,NX); % The initial condition: all of wavefield values are null before source excitation. 波场在z方向上的速度分量初始条件
Ux = zeros(NZ,NX); % The initial condition: all of wavefield values are null before source excitation. 波场在x方向上的速度分量初始条件
Vz = zeros(NZ,NX); % The initial condition: all of wavefield values are null before source excitation. 波场在z方向上的位移分量初始条件
Vx = zeros(NZ,NX); % The initial condition: all of wavefield values are null before source excitation. 波场在x方向上的位移分量初始条件
Psum = NaN*ones(Nz,Nx); % 存储波场在不同时间步长上的压力分量的累积和
U = NaN*ones(nz,nx,nt); % 用于存储完整的波场数据
% tic;
for it = 1:1:nt
Ux(nsrcz,nsrcx) = Ux(nsrcz,nsrcx) + ampl*src(it)./2;
Uz(nsrcz,nsrcx) = Uz(nsrcz,nsrcx) + ampl*src(it)./2;
Ut(:,:) = Ux(:,:) + Uz(:,:);
U(:,:,it) = Ut(znodes,xnodes);
end
% toc;
syngram(:,:) = U(1,xrcvr,:);
singleRec = syngram';
singleRec = downsample(singleRec,5); % 下采样
end
% 实验
6、我的疑问:
1)评价指标,目前论文SSIM、MAE、RMSE, 地质勘探的角度,有什么评价指标?尤其在自然数据中,工程应用场景下,更希望通过FWI提供什么信息?
2)盐体数据中,地层很薄,对这类的识别是否很重要?
3)地震数据的噪声来源:采集设备、地理环境,哪些噪声对地震数据的影响特别大?
4)地震数据采集后,到目前拿到手上的数据,中间是否经过了别的处理?这种处理是否是加入噪声,或者减少信息量的。