计算机中各种进制之间的相互转换过程
一.进制的由来
1.定义
进制也就是进位计数制,是人为定义的带进位的计数方法(有不带进位的计数方法,比如原始的结绳计数法,唱票时常用的“正”字计数法,以及类似的tally mark计数)。 对于任何一种进制---X进制,就表示每一位上的数运算时都是逢X进一位。 十进制是逢十进一,十六进制是逢十六进一,二进制就是逢二进一,以此类推,x进制就是逢x进位。
进位制/位置计数法是一种记数方式,故亦称进位记数法/位值计数法,可以用有限的数字符号代表所有的数值。可使用数字符号的数目称为基数,基数为n,即可称n进位制,简称n进制。现在最常用的是十进制。
2.二进制
二进制有两个特点:它由两个数码0,1组成,二进制数运算规律是逢二进一。
为区别于其它进制,二进制数的书写通常在数的右下方注上基数2,或在后面加B表示。
例如:二进制数10110011可以写成(10110011)2,或写成10110011B。
3.八进制
由于二进制数据的基数R较小,所以二进制数据的书写和阅读不方便,为此,在小型机中引入了八进制。八进制的基数R=8=2^3,有数码0、1、2、3、4、5、6、7,并且每个数码正好对应三位二进制数,所以八进制能很好地反映二进制。
八进制用下标8或数据后面加O表示,例如:八进制数据: (352.264)8或352.264O或者(427.351)O。
4.十进制
由于人类解剖学的特点,双手共有十根手指,故在人类自发采用的进位制中,十进制是使用最为普遍的一种。
十进制的基数为10,数码由0-9组成,计数规律逢十进一。例如:十进制数据:(159)10或者(967)D。
5.十六进制
由于二进制数在使用中位数太长,不容易记忆,所以又提出了十六进制数。
十六进制数有两个基本特点:它由十六个数码:数字0~9加上字母A-F组成(它们分别表示十进制数10~15),十六进制数运算规律是逢十六进一,即基数R=16=2^4,通常在表示时用尾部标志H或下标16以示区别,在c语言中用添加前缀0x以表示十六进制数。
例如:十六进制数4AC8可写成(4AC8)16,或写成(4AC8)H。
由此我们可以知道各进制的由来与产生效果的不同了。
二.R进制数转换为十进制数
R进制转换成十进制:
方法就是按权展开相加(系数乘以基数的权次方相加)
系数:就是就是每一位上的数
基数:R进制的基数就是R
权:从右侧开始每一位的索引值从0开始,每一位对应的索引值就是权值.
(1)二进制数转换为十进制数
例:将一个二进制数 (10101)B = (____)D
在二进制数10101中,共有五位系数。计算应从低位到高位依次乘以2的i次方最后相加( i为每一位数字的权重,它是随着低位向高位的进发而每增加1,直到没有系数为止)。
(10101) B= 1*2^4+0*2^3+1*2^2+0*2^1+1*2^0=1+0+4+0+16=21
所以 (10101) B= (21) D
例:将一个二进制带小数(1101.01) B=(______) D
对于二进制数带小数,以整数的最低位索引权重0为界限,整数部分是大于0的正整数且从右向左,从低位到高位按权分配;而小数部分则是小于0的负整数且从左向右,从高位到低位按权分配的。
( 1101.01 ) 2 = 1× 2^3 + 1× 2^2 + 0× 2^1 + 1× 2^0 + 0×2^(-1) + 1×2^(-2) = 8 + 4 + 1 + 0.25 = 13.25
所以 (1101.01) B= (13.25) D
(2)八进制转十进制
同理,八进制转换十进制也是每一位乘以8的i次方最终相加而成得到结果。
例如: ( 267.5 ) 8 = (_____) D
( 267.5 ) 8 = 2 × 8^2 + 6 × 8^1 + 7 × 8^0 + 5 × 8^(-1) = 128 + 48 + 7 + 0.625 = 183.625
所以 ( 267.5 ) 8 =(183.625) D
(3)十进制的安全展开图
(4)十六进制转换十进制
16进制数共有16位数码,∈{ 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F}
A代表10,B代表11,C代表12,D代表13,E代表14,F代表15
例如: ( 4 A 8 F .5 ) H =(_______)D
( 4 A 8 F.5 ) H = 4×16^3 + 10×16^2 + 8×16^1 + 15×16^0 + 5×16^(-1) = 16384 + 2560 + 128 + 15 + 0.3125 = 19087.3125
所以( 4 A 8 F.5 ) H =(19087.3125)D
再次总结一句话:R进制转换十进制的口诀就是方法就是按权展开相加(系数乘以基数的权次方相加)。
三.十进制转换R进制
十进制转换R进制时,方法步骤:
1.将十进制整数转换成R进制整数采用“除R取倒余法”。即将十进制整数除以R,得到一个商和一个余数;再将商除以R,又得到一个商和一个余数; 以此类推,直到商等于零为止。每次得到的余数的倒排列,就是对应R进制数的各位数。
2. 十进制小数转换成R进制小数。十进制小数转换成R进制小数是用“乘R取整法”。即用R逐次去乘十进制小数,以此类推,直到余数为1停止。将每次得到的积的整数部分按各自出现的先后顺序依次排列(与整数的排列顺序相反),就得到相对应的R进制小数。
(1)十进制转二进制--(小数部分除二取余,逆序排列,小数部分乘2取整,顺序排列)
例:将25转换为二进制数
解:25÷2=12 余数1
12÷2=6 余数0
6÷2=3 余数0
3÷2=1 余数1
1÷2=0 余数1 最终将余数倒着写出来即可!
所以(25) 10 =(11001)2
例:将(25.125)D==转换为二进制数
解:整数部分25的计算如上 :(25) 10 =(11001)2
小数部分:0.125 *2=0.25......整0
0.25 *2 =0.50……整0
0.50*2=1.0……整1
所以(0.125) D=(0.001) B,与整数相加而成就是(25.125) 10 =(11001.001)2
(2)十进制转换八进制(整数部分除八取余,逆序排列,小数部分乘八取整,顺序排列)
例:将十进制数1000,转换为八进制数。
解:1000/8=125,余数为0;
125/8=15,余数为5;
15/8=1,余数为7;
1/8=0,余数为1;
从上往下看这些余数,逆序写出就是1750,要注意的是最后一定要除到0为止,也就是最后一步1/8=0,一定要除到0.
所以(1000) D=(1750) O
(2)十进制转换十六进制(整数部分除十六取余,逆序排列,小数部分乘十六取整,顺序排列)
例: 将十进制数(0.9032) D转化成16进制小数
解: 0.9032*16=14.4512 取整数14 即E
0.4512*16=7.2192 取整数7
0.2192*16=3.5072 取整数3
0.5072*16=8.1152 取整数8
0.1152*16=1.8432 取整数1
所以:(0.9032) D= (0.E7381) H
四.二八进制的相互转换
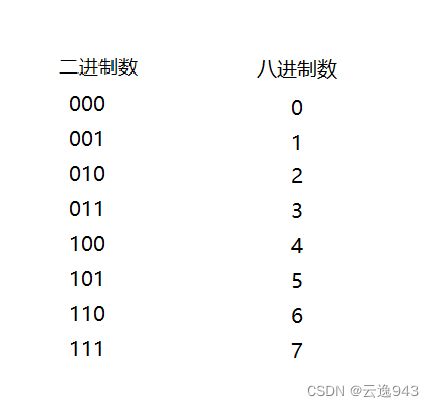
1、先了解二进制数与八进制数之间的对应关系。
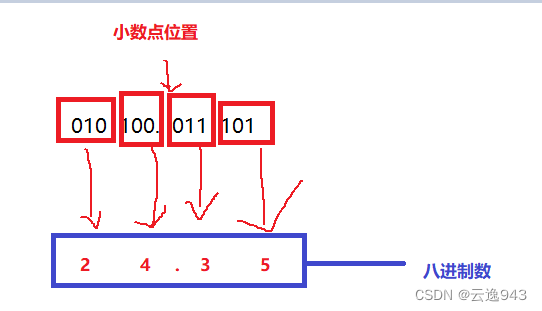
2、二进制转换成八进制的方法是,取三合一法,即从二进制的小数点为分界点,向左(或向右)每三位取成一位。
3、分好组以后,对照二进制与八进制数的对应表,将三位二进制按权相加,得到的数就是一位八进制数,然后按顺序排列,小数点的位置不变,最后得到的就是八进制数。
4、这里需要注意的是,在向左(或向右)取三位时,取到最高位(最低位)如果无法凑足三位,就可以在小数点的最左边(或最右边)补0,进行换算。
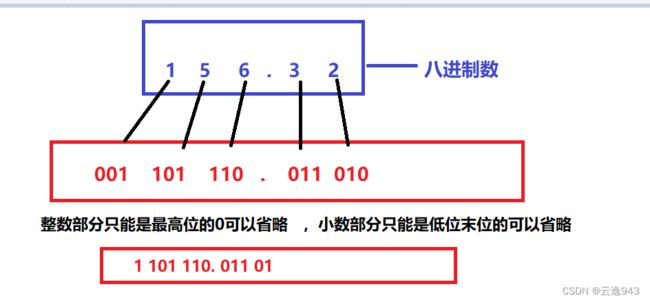
下面看看将八进制转为二进制,反过来啦,方法就是一分三,即一个八进制数分成三个二进制数,用三位二进制按权相加,最后得到二进制,小数点依旧就可以了。
五.二进制与十六进制的相互转换
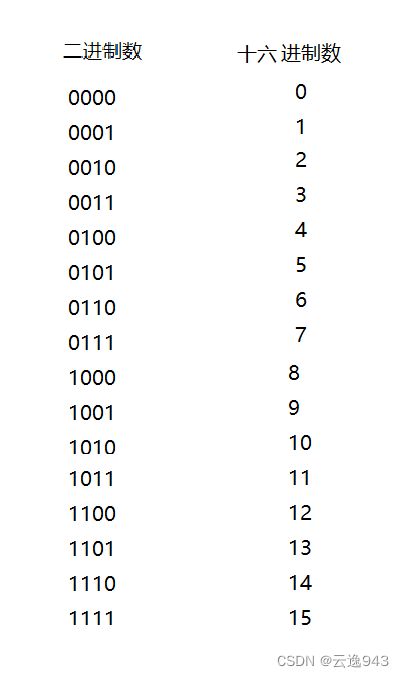
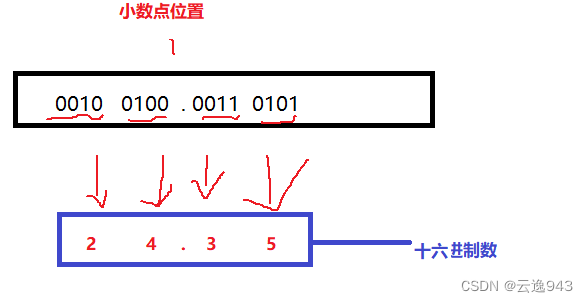
1.二进制数与十六进制数之间的对应关系。
2.二进制转换成十六进制的方法是,取四合一法,即从二进制的小数点为分界点,向左(或向右)每四位取成一位。
3. 分好组以后,对照二进制与十六进制数的对应表,将四位二进制按权相加,得到的数就是一位十六进制数,然后按顺序排列,小数点的位置不变,最后得到的就是十六进制数。
4. 在向左(或向右)取四位时,取到最高位(最低位)如果无法凑足四位,就可以在小数点的最左边(或最右边)补0,进行换算,与八进制同理。
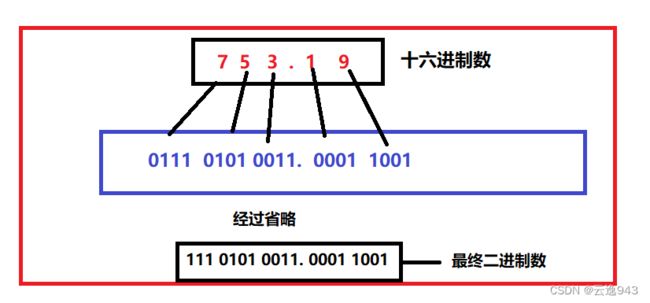
5. 十六进制转为二进制,反过来啦,方法就是一分四,即一个十六进制数分成四个二进制数,用四位二进制按权相加,最后得到二进制数。
六.八进制与十六进制的相互转换
八进制与十六进制相互转换时,需要用到中间值--二进制,二进制是八进制与十六进制相互转换的桥梁。这样做不仅方便,而且不易出错。具体的就不再进行过多讲解了。
八进制转换十六进制:
八进制==>二进制==>十六进制
十六进制转换八进制:
十六进制==>二进制==>八进制
好了,进制的转换就讲到这里,大家觉得有用的话,关注关注点个赞吧!!