7-2 Color the Tree （PAT ADSAA）

#include 
#include 
#include 
#include 

题目如下：

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

• (1) Every node is either red or black.
• (2) The root is black.
• (3) Every leaf (NULL) is black.
• (4) If a node is red, then both its children are black.
• (5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

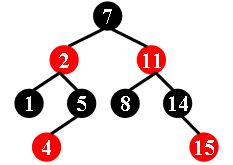
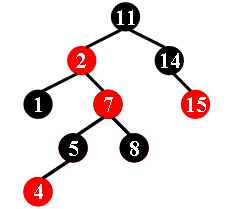
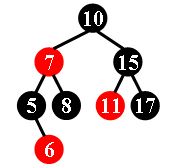
For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.

Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is possible to color the nodes and turn it into a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤10) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary search tree. The second line gives the postorder traversal sequence of the tree. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print in a line Yes if the given tree can be turned into a legal red-black tree, or No if not.

Sample Input:

3
9
1 4 5 2 8 15 14 11 7
9
1 4 5 8 7 2 15 14 11
8
6 5 8 7 11 17 15 10

Sample Output:

Yes
No
Yes