树状数组(入门附模板)
声明:本篇文章图片非原创
目录
简介
lowbit函数
结构分析
单点修改,区间查询
区间修改,单点查询
区间修改,区间查询
模板题
树状数组1–单点修改,区间查询
题目描述
输入格式
输出格式
输入输出样例
输入 #1
输出 #1
说明/提示
分析
代码
树状数组2––区间修改,单点查询
题目描述
输入格式
输出格式
输入输出样例
输入 #1
输出 #1
说明/提示
样例 1 解释:
数据规模与约定
分析
代码
最强编译器推荐
简介
树状数组或二叉索引树(英语:Binary Indexed Tree),又以其发明者命名为Fenwick树,最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率(Cumulative Frequency)的计算问题,现多用于高效计算数列的前缀和, 区间和。 ——源自百度百科
百度百科太过于学术化,看不懂?怎么办?总的来说,树状数组是一种支持单点修改,区间查询的一种代码量小的数据结构。
那么树状数组和线段树有什么区别呢?
- 线段树的码量很明显比树状数组多
- 线段树可以进行区间修改和区间查询,然而树状数组是线段树的低级版本,可以进行区间查询,但只能一次性改一个点,当然,经过改造后的树状数组可以进行区间修改,我们今天先讲树状数组的低级版本。
如上图,这就是树状数组的形式,仔细看一看,你会发现树状数组是不规则的叉树。下图是线段树的样子
两者还是有很多地方是不一样的。
lowbit函数
要想学会树状数组,我们必须要理解一个函数:lowbit()
lowbit()就是求一个数与上他的相反数,简单来说,就是x&(-x)
想要算lowbit(x)很简单,举个栗子:
假设一个数 x=5,5的二进制编码为0101。根据我们的二进制原理,则-x也就是1011,所以x&(-x)=1,如果你再举几个例子,细心地你就会发现,x的二进制编码的第一个1的位置就是lowbit(x)的值?
下面给出lowbit的函数模板
//version 1
int lowbit(int x){
return x&(-x);
}
//version 2
#define lowbit(x) x&(-x) 结构分析
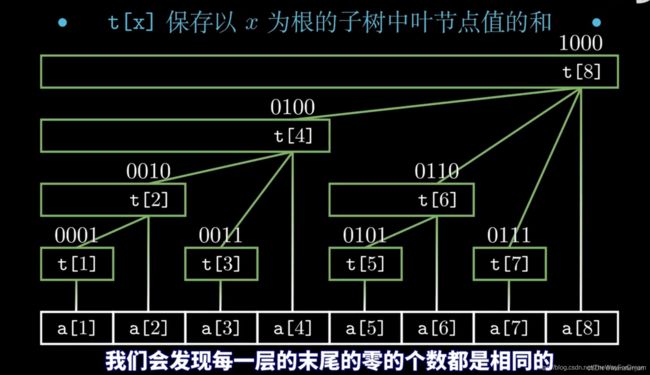
先放一张图片
看了这一张图片,我们会发现,每一层的下表的二进制编码末尾的0的个数都是相同的,而且是从下至上一次递增的。
那么原数组前4项的和t[4]=t[2]+t[3]+a[4]=t[1]+a[2]+t[3]+a[4]=a[1]+a[2]+a[3]+a[4]
看了这一张图片之后,你是不是发现了更多的奥秘了呢? 树状数组中节点x的父节点为x+lowbit(x),例如t[2]的父节点为t[4]=t[2+lowbit(2)].
当你理解了这些之后,就可以尝试一下编写代码了.
单点修改,区间查询
我们消化了上面的内容之后,会发现,编写树状数组的代码会变得尤为简单.在这里,我们先来看一下如何在树状数组里进行单点修改,区间查询.
如果我们将a数组进行+k操作,那么它的父亲节点都要加上一个k. 举个栗子:如果我们要将a[1]数组进行+k操作,那么如上图t[1],t[2],t[4],t[8]都要加上一个k(因为我们是用差分建的数,所以更改单点的值时也要牵扯到它的祖宗).
此时,我们就要运用到我们前面学的lowbit函数了!下面是单点修改的代码
int one_change(int x,int k){
for(int i=x;i<=n;i+=lowbit(i)){
t[i]+=k;
}
}
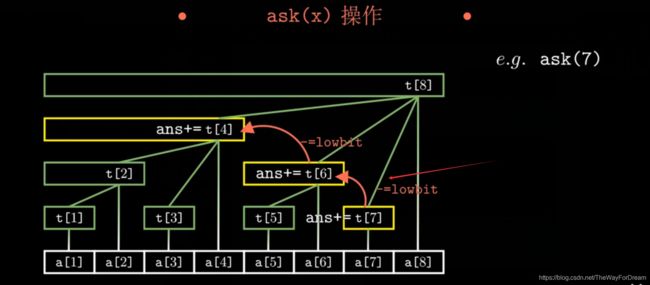
扯完了单点修改,我们继续来扯一下区间查询,区间查询又是什么呢,看一张图片,估计你们就明白了.
图上求的是前7项的和ask[7]. 从图上也不难看出,ans[7]=t[7]+t[6]+t[4].如果你在多找几个例子,你会发现,所求前缀和的下标一次减去一个lowbit.所以,在代码中,我们可以进行使用lowbit来去求前缀和.接下来就是区间求和的代码
int find(int x){
int sum=0;
for(int i=x;i>=1;i-=lowbit(i)){
sum+=t[i];
}
return sum;
}
这时,喜欢刨根问底的你们就会给出一个很好地问题:上面这段代码只能实现[1,x]的区间求和,那么我想求[l,r]区间的和怎么办呢?此时就要用到前缀和的相减思想了(如果你们还没学会前缀和,那就停下这篇博客,赶快去学习前缀和吧).以下是更新后的代码.
int lrfind(int l,int r){
int sum=0;
for(int i=l;i>=1;i-=lowbit(i)){
sum+=t[i];
}
for(int i=r-1;i>=1;i-=lowbit(i)){
sum-=t[i];
}
return 0;
}
区间修改,单点查询
我们讲完了单点修改,区间查询,现在就来讲解一下区间修改,单点查询.
对于这一类操作,我们需要构造出原数组的差分数组,然后用树状数组维护该数组就行了
如果要进行区间修改的话,我们只需要对差分数组进行操作就行了,例如对[l,r]区间进行+k操作,那么我们只需要更新差分数组change(l,k),change(r+1,-k)就行了,这是差分数组的性质.听懂了吗?下面是区间修改的代码
void lrchange(int pos,int k){
for(int i=pos;i<=n;i+=lowbit(i)){
t[i]+=k;
}
}
lrchange(l,k);
lrchange(r+1,-k);
如果进行单点查询操作,只需要求b数组的前缀和就行了,别忘了我们是根据差分建的树.下面是单点查询操作的代码
int one_find(int pos){
int ans=0;
for(int i=pos;i;i-=lowbit(i)){
ans+=t[i];
}
return ans;
}
区间修改,区间查询
若此模板使用树状数组过于复杂,不如使用高效的线段树进行解题.
模板题
树状数组1–单点修改,区间查询
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含n个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来 m 行每行包含 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x个数加上k -
2 x y含义:输出区间[x,y]内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
输入输出样例
输入 #1
5 5 1 5 4 2 3 1 1 3 2 2 5 1 3 -1 1 4 2 2 1 4
输出 #1
14 16
说明/提示
【数据范围】
对于 30%30% 的数据,1≤n≤8,1≤m≤10;
对于 70%70% 的数据,1≤n,m≤104;
对于 100%100% 的数据,1≤n,m≤5×105。
数据保证对于任意时刻,a 的任意子区间(包括长度为 1 和 n 的子区间和均在 [−231,231) 范围内。
样例说明:
故输出结果14、16
分析
此题就是模板题,直接套模板上去就行了
代码
#include
#define lowbit(x) (x&(-x))
using ll=long long;
using namespace std;
int c[2000006],n,m,x;
long long ans;
int one_change(int x,int k){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=k;
}
}
void lrfind(int l,int r){
for(int i=r;i>=1;i-=lowbit(i)){
ans+=c[i];
}
for(int i=l-1;i>=1;i-=lowbit(i)){
ans-=c[i];
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>x;
one_change(i,x);
}
for(int i=1;i<=m;i++){
int p,xx,yy;
cin>>p>>xx>>yy;
if(p==1){
one_change(xx,yy);
}else{
ans=0;
find(x,y);
cout< 树状数组2––区间修改,单点查询
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 x;
-
求出某一个数的值。
输入格式
第一行包含两个整数 N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含 N 个用空格分隔的整数,其中第 i个数字表示数列第 i 项的初始值。
接下来 M 行每行包含 2 或 4个整数,表示一个操作,具体如下:
操作 1: 格式:1 x y k 含义:将区间 [x,y] 内每个数加上k;
操作 2: 格式:2 x 含义:输出第 x 个数的值。
输出格式
输出包含若干行整数,即为所有操作 2的结果。
输入输出样例
输入 #1
5 5 1 5 4 2 3 1 2 4 2 2 3 1 1 5 -1 1 3 5 7 2 4
输出 #1
6 10
说明/提示
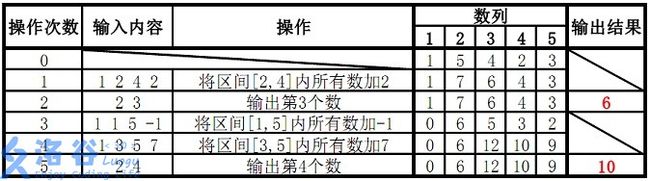
样例 1 解释:
故输出结果为 6、10。
数据规模与约定
对于 30% 的数据:N≤8,M≤10;
对于 70%的数据:N≤10000,M≤10000;
对于 100%100% 的数据:1≤N,M≤500000,1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 230。
分析
同样是模板题,没有什么可以分析的,直接把代码套上去就行了
代码
#include
using namespace std;
#define lowbit(x) x&(-x)
using ll=long long;
long long n,q,f,a[1000005],l,r,x,p,b[1000005];
long long c[1000005];
int main(){
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];
for(int j=i;j<=n;j+=lowbit(j)){
c[j]+=b[i];
}
}
for(int i=1;i<=q;i++){
cin>>f;
if(f==1){
cin>>l>>r>>x;
for(int j=l;j<=n;j+=lowbit(j)){
c[j]+=x;
}
for(int j=r+1;j<=n;j+=lowbit(j)){
c[j]-=x;
}
}else{
cin>>p;
long long ans=0;
for(int j=p;j>=1;j-=lowbit(j)){
ans+=c[j];
}
cout< 最强编译器推荐
到了最后,我给大家伙们推荐一个超好用的编译器(无论在什么系统上都可以)
https://lightly.teamcode.com/