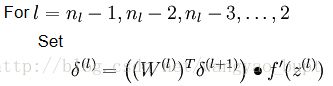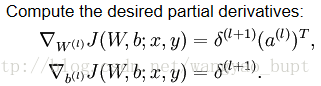Python实现神经网络Part 3: 多层全连接神经网络

主旨

本文将描述如何用Python实现多层全连接神经网络。

本系列第一篇和第二篇都是以一个神经元为基本单位用Python实现功能并对前向计算和误差反向传播做实验分析。但是在实际的使用中，单个神经元是无法作为“深度神经网络”使用的，为了实现深度学习，网络除了输入层和输出层，至少要包含若干隐层。因此，本文将练习使用Python实现一个可以包含任意多层，每层任意节点数目的神经网络。

索引

本文是本系列第三篇，本系列介绍见Python实现神经网络Part 1: 实现forward和BP算法的神经元

源代码

我的GitHub上SimpleNeuralNetwork项目中FullConnectedNetwork2.py

理论模型

目前（2017年3月）网络上关于神经网络的各类理论教材已经非常丰富，本文选择斯坦福大学的如下两篇讲义作为理论参考，即符号体系、损失函数、梯度推导全部沿用这两篇文章的描述。

• Neural_Networks[1]
• Backpropagation_Algorithm[2]

数学符号约定

L : 神经网络总层数, 为了实现深度学习效果，除了输入层和输出层之外至少有一个隐层，因此约定 L>=3
l ：任意一层的层序号，l∈{0,1,2,...,L−1}, 其中第 0 层为输入层，第L−1层为输出层。
Sl : 第 l 层节点数目，Sl>=1。每一层内的节点由0到 Sl−1 顺序编号
w(l)ij : 从第 (l) 层序号 (j) 指向第 (l+1) 层序号 (i) 的连接的权重因子
W(l) : 由 w(l)ij 组成的矩阵，其中 i∈{0,1,..Sl+1} , j∈{0,1,..,Sl} ，即

W(l)=⎡⎣⎢⎢⎢⎢⎢⎢w(l)00w(l)10...w(l)Sl+10w(l)01w(l)11...w(l)Sl+11............w(l)0Slw(l)1Sl...w(l)Sl+1Sl⎤⎦⎥⎥⎥⎥⎥⎥

bias(l)i : 第 (l+1) 层序号 (i) 的节点的偏置量
bias−→−(l) : 第 (l+1) 层偏置量向量,

bias−→−(l)=(bias(l)0,bias(l)1,...,bias(l)Sl+1)T

z(l+1)i : 第(l+1)层，第i个节点，激活函数之前的计算值

z(l+1)i=∑j=0Sl−1(w(l)ij∗a(l)j)+bias(l)i

定义 z(0)i 不存在

a(l+1)i : 第(l+1)层，第i个节点，激活函数的输出

a(l+1)i=activation_function(z(l+1)i)

定义 a0i 为输入向量的第i个维度

本文中约定激活函数为sigmoid，因此上式可以写为

a(l+1)i=sigmoid(z(l+1)i)

δ(l)i : 第l层第i个节点的误差因子，教材[2]中解释如下

Then, for each node i in layer l, we would like to compute an “error term” that measures how much that node was “responsible” for any errors in our output

数据结构定义

如何存储网络结构？即共有多少层，每层多少个节点。实现代码和注释如下

# @param iStructure is a list containing L enlements, representing L layers of a fully connected netowrk
# The 1st element (aka iStructure[0]) define number of input nodes
# the i-th element (aka iStructure[i-1]) define number of neural nodes in i-th layer
  self.networkStructure = iStructure

如何存储神经网络中的权重和偏置值？参考上一节“数学符号约定”，全连接神经网络相邻的两层之间存在权重矩阵和偏置向量，为了运算方便，我们可以将他们合二为一，称为权重和向量矩阵

Weight_and_Bias_Matrix(l)=[W(l):bias−→−(l)]

整个网络中存在多个权重矩阵，因此使用List保存，即如下代码中的self.weightMatrixList，这个List中每一个元素对应 Weight_and_Bias_Matrix(l)

 #weightMatrixList is a container of Weight Matrixes of each layer
    self.weightMatrixList = np.ndarray((self.numberOfLayers - 1),np.object)
    for layerIdx in range(0, self.numberOfLayers - 1):
     weightMatrixBetweenCurAndNextLayer = np.random.randn(
          iStructure[layerIdx+1],iStructure[layerIdx]+1)        
     self.weightMatrixList[layerIdx] = weightMatrixBetweenCurAndNextLayer

每一层激活值保存在self.activationValueMatrix中，这里每一层的激活值组成一个向量，L层激活值组成矩阵，因此称为activationValueMatrix

    # activationValueMatrix is activation values of each layer in each sample in a batch,
    # activationValueMatrix's shape is (batchSize, numberOfLayers), each element is an 1-D vector,
    # For example, given batchIdx = b, LayerIndex = l, the activationValueMatrix[b][l] represents
    #  the value (1-D vector with self.networkStructure[l] dims) calculated from l-th layer
    # For the input layer, activationValueMatrix[b][0] = inputVector
    self.activationValueMatrix = np.ndarray((self.batchSize, len(self.networkStructure)), np.object)

前向计算

按照神经网络定义计算即可，对于每一层

z→(l+1)=[W(l):bias−→−(l)]∗(a(l)0,a(l)1,...,a(l)SL,1)T

a→(l+1)=sigmoid(z→(l+1))

a→(L−1) 就是神经网络的输出向量

关键实现代码如下

    result =np.ndarray((batchSize, self.networkStructure[-1]))
    for sampleIdx in range(0, batchSize):
      #the a[sampleIdx][0] always equal to inputVector
      self.activationValueMatrix[sampleIdx][0] = inputData[sampleIdx]
      for layerIdx in range(1, self.numberOfLayers):
        activation_and_one = np.ones(self.activationValueMatrix[sampleIdx][layerIdx - 1].shape[0]+1)
        activation_and_one[:-1] = self.activationValueMatrix[sampleIdx][layerIdx - 1]
        self.zMatrix[sampleIdx][layerIdx] \
          = np.matmul(self.weightMatrixList[layerIdx - 1], activation_and_one)
        self.activationValueMatrix[sampleIdx][layerIdx] = self.sigmoid(self.zMatrix[sampleIdx][layerIdx])
      result[sampleIdx] = self.activationValueMatrix[sampleIdx][self.numberOfLayers-1]

误差反向传播和参数训练

根据教材[2]，误差反向传播和参数训练的关键是计算出最终误差对每个参数（权重和bias）的梯度，梯度计算过程如下

首先，对于输出层计算 δ(nl) ，其中 nl=L ，计算方式由[2]给出，如下所示

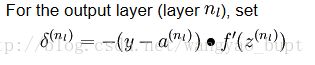
实现代码

    # for each node i in layer l, we would like to compute an "error term"  that measures
    # how much that node was "responsible" for any errors in our output
    # delta represent such error
    delta = np.ndarray((self.batchSize, self.numberOfLayers-1), np.object)

    ## calculate deritives of each weight/bias at each node in eachlayer in each sample
    for sampleIdx in range(0, self.batchSize):
      delta[sampleIdx][-1] = \
        -(label[sampleIdx] - self.activationValueMatrix[sampleIdx][self.numberOfLayers-1])\
        *self.dsigmoiddx_usingActivationValue(self.activationValueMatrix[sampleIdx][self.numberOfLayers-1])

第二，计算其他层的 δ ，计算方法在教材[2]中描述如下

实现代码如下

 for sampleIdx in range(0, self.batchSize):
      delta[sampleIdx][-1] = \
        -(label[sampleIdx] - self.activationValueMatrix[sampleIdx][self.numberOfLayers-1])\
        *self.dsigmoiddx_usingActivationValue(self.activationValueMatrix[sampleIdx][self.numberOfLayers-1])
      for layerIdx in range(self.numberOfLayers-3, -1, -1):
        #build vector for f'(z_i)
        dsigmoidVector = np.zeros(self.networkStructure[layerIdx+1])
        for nodeIdx in range(0, self.networkStructure[layerIdx+1]):
          dsigmoidVector[nodeIdx] = self.dsigmoiddx_usingActivationValue(self.activationValueMatrix[sampleIdx][layerIdx+1][nodeIdx])
        # build weight matrix, remove bias column
        weightMatrix = self.weightMatrixList[layerIdx];
        weightMatrix = np.zeros((self.weightMatrixList[layerIdx].shape[0],self.weightMatrixList[layerIdx].shape[1]-1) )
        for rowIdx in range(0, weightMatrix.shape[0]):
          for colIdx in range(0, weightMatrix.shape[1]):
            weightMatrix[rowIdx][colIdx] = self.weightMatrixList[layerIdx][rowIdx][colIdx]
        weightMatrix = np.transpose(weightMatrix)
        #calculate delta
        delta[sampleIdx][layerIdx] = np.matmul(weightMatrix, delta[sampleIdx][layerIdx+1]) * dsigmoidVector

第三，计算梯度，教材推导出的公式如下

我的代码实现如下

      for layerIdx in range(0, self.numberOfLayers-1):
        ## dWeightAndBias is value of desired partial derivatives
        dWeightAndBias = np.zeros(self.weightMatrixList[layerIdx].shape)
        for i in range(0, self.weightMatrixList[layerIdx].shape[0]):
          for j in range(0, self.weightMatrixList[layerIdx].shape[1]):
            if j >= self.networkStructure[layerIdx]:
              #dbias
              dWeightAndBias[i][j] = delta[sampleIdx][layerIdx][i]
            else:
              dWeightAndBias[i][j]  = delta[sampleIdx][layerIdx][i] \
                                             * self.activationValueMatrix[sampleIdx][layerIdx][j];

有了梯度之后，就可以对每一个权重系数和偏置系数做梯度下降更新。