卷积计算加速方法--slice卷积
文章目录
-
- 1、前言
- 2、分块卷积存在的问题
- 3、分块卷积问题的解决方案--slice卷积
- 4、slice卷积每层所需切分尺寸计算
- 4、结论及加速效果
1、前言
我们在上一篇卷积计算加速方法中讨论过,当卷积的输入太大导致内存不够用时,考虑将一大块卷积分成多个小块分别进行卷积,相当于将原始输入分成几个小的输入经过同一组卷积核分别卷积,每块之间互不影响,其中每块小的输入都是原始输入的子集,最后将结果合并,实现分块卷积的输出结果与整个输入卷积后的结果完全一致,这种分块卷积的算法可以减小内存消耗同时大大提高运行效率。不了解的可以先看看这篇博文:卷积计算加速方法–分块卷积。但是这种算法有个问题,如果单纯的简单划分的话卷积到后面会越来越少,也就是说会有信息损失。因此在分块的时候会有overlap的出现,并且这个overlap会随着层数的增加会累积。
2、分块卷积存在的问题
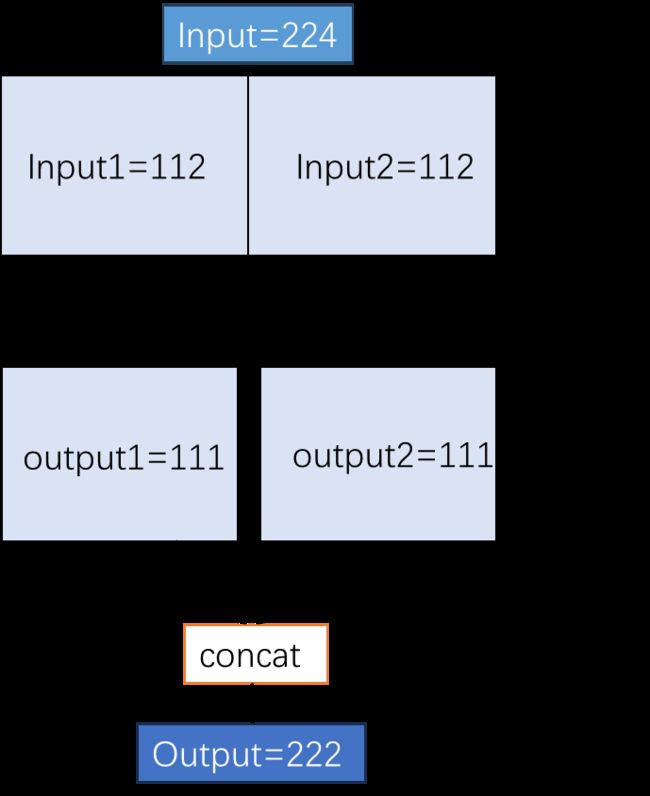
由第一节我们知道,分块卷积的做法会有overlap的出现,并且会随着层数的增加累积,如下图当kernel_size=3,stride=1,padding=1,分块的块数block=2时,一层卷积的时候overlap为1,两层卷积时累积到了2 … … 。

从上图可以看到,随着层数的增加,overlap的尺寸也会增加,而且会随着层数累积,那就可能会出现一个问题。即层数很多时,这个overlap累积的尺寸非常大,甚至大过其他块的输入,那就根本实现不了卷积同时也没有实现计算的加速。
3、分块卷积问题的解决方案–slice卷积
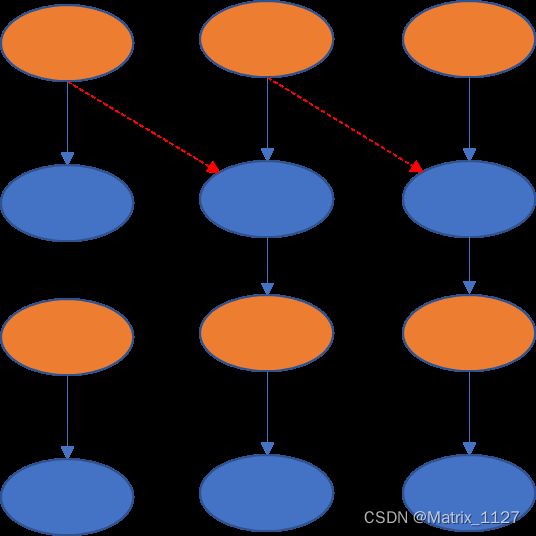
下面考虑怎么解决这个问题,由于这个问题是随着层数增加而出现的,那么如果每层单独解决overlap的问题,不把这个overlap往上传递是不是就解决了这个问题呢?答案是肯定的,这就是我们本文要讲的slice卷积,每层分块的时候左边加上一些overlap,然后将卷积之后的结果slice一部分给右边的一块,保证他们的结果合并后和普通卷积结果一致,并且每层之间互不影响。
4、slice卷积每层所需切分尺寸计算
先按普通卷积的步骤算出每层的输出,然后将最后一层的输出分块,并对每一个分块往上倒推,将每一层的slice尺寸往后面一块添加,需要注意,如果stride大于1,普通卷积会与除不尽的情况,也就是可能会有几个像素点丢失,倒推的时候记得将这几个丢失的像素点找回来,并且由于丢失的像素点是在最后一个滑窗上面,所以像素点找回来的时候也要加在最后一块上。下面代码实现了求每层slice尺寸的功能。
def unit_allocation(alist, num, block): # 递归分块函数
if block == 1:
alist.insert(len(alist)//2, num)
return alist
elif block == 2:
alist.insert(len(alist)//2, num//2)
alist.insert(len(alist)//2, num - (num//2))
return alist
alist.insert(len(alist)//2,num//block)
alist.insert(len(alist)//2,num//block)
return unit_allocation(alist,num - (num//block * 2),block - 2)
def reverse_input(block = 2, params_file = "slice_params.csv"):
"""计算每层卷积slice尺寸的函数
主要功能:当卷积的参数量太大导致内存不够用时,考虑分成几块进行卷积,然后将第一块的一部分slice给第二块,
保证第二块卷积加上第一块的slice部分刚好是对的,第二块、第三块以此类推;最后将结果合并,可以减小
内存消耗同时大大提高运行效率,这个函数就是用来计算所需slice的尺寸。
params:
unit:切分块数.
file:各层卷积或反卷积所需的相应参数.
file::(kernel_size,stride,padding):每层卷积所需的参数尺寸.
unit_allocation:递归分块函数,每块尺寸比整除方式更平均.
return:
slice方法进行卷积每层所需slice的尺寸.
"""
params = []
with open(params_file,"r") as file:
for line in file.readlines():
params.append(line.replace("\n","").split(","))
print("输入卷积的各层参数:")
print("input_size = {0}".format(params[1][0]))
for i in range(2, len(params)):
print(params[i])
print("\t" + "-"*80)
k_size = []
stride = []
padding = []
slice_size = [] # 保存倒推每层需要slice的尺寸
reverse_size = [] # 保存正推往下每层的尺寸
forward_size = [int(params[1][0])] # 保存倒推往上每层的尺寸
for i in range(3,len(params)):
k_size.append(int(params[i][0]))
stride.append(int(params[i][1]))
padding.append(int(params[i][2]))
for i in range(0,len(params) - 3):
forward_size.append((forward_size[i] - k_size[i] + 2*padding[i])//stride[i] + 1)
layers = len(k_size)
_unit_size = []
unit_allocation(_unit_size, forward_size[-1], block) # 递归平均分块,也可对unit_size手动指定分块
reverse_size.append(_unit_size)
for i in range(layers - 1,-1,-1):
reverse0 = (reverse_size[layers - i - 1][0] - 1)*stride[i] + k_size[i] - padding[i]
remainder = (forward_size[i] - k_size[i] + 2*padding[i])%stride[i]
_slice = [k_size[i] - stride[i]]
_reverse = [reverse0]
slice_size.append(_slice)
for j in range(1, block - 1):
reverse_j = (reverse_size[layers - i - 1][j] - 1)*stride[i] + k_size[i] - slice_size[layers - i - 1][j - 1]
_reverse.append(reverse_j)
reverse1 = (reverse_size[layers - i - 1][-1] - 1)*stride[i] + k_size[i] - padding[i] + remainder - slice_size[layers - i - 1][-1]
_reverse.append(reverse1)
reverse_size.append(_reverse)
# 打印输出,将每一层前后需要slice的尺寸打印出来
print("正向每层的输出尺寸\t逆向倒推slice及输出的尺寸")
output = [reverse_size[0]]
slice_size.insert(0, [0, 0])
for i in range(1, layers + 1):
_out = []
layer_out0 = repr(reverse_size[i][0])
_out.append(layer_out0)
for j in range(1, block - 1):
layer_out_j = "(" + repr(slice_size[i][j - 1]) + ")+" + repr(reverse_size[i][j])
_out.append(layer_out_j)
layer_out1 = "(" + repr(slice_size[i][-1]) + ")+" + repr(reverse_size[i][-1])
_out.append(layer_out1)
output.append(_out)
for i in range(len(output)):
print(" 第{0}层: {1}\t\t{2}".format(i+1, forward_size[i], output[len(output) - i - 1]))
reverse_input(block = 3, params_file = "slice_params.csv")
例如输入为[1, 3, 224, 224],连着三层卷积,第一层参数为:kernel_size=3,stride=1,padding=1;第二层参数为:kernel_size=3,stride=2,padding=1;第三层参数为:kernel_size=4,stride=2,padding=1。经过三层卷积后输出尺寸为56。
先计算每层普通卷积往下的尺寸,然后将最后一层分块成3份[18,20,18],倒推向上推出每层后面一块需要从前面一块slice过来的像素尺寸,结果如下图所示。从下图可以看出,如果第一层输入为[75,(2)+80,(2)+69]时,其中(2)表示从前面slice 2个像素点到后面,第一层卷积后的结果再将第一块slice一个像素给第二块,第二块slice一个像素给第三块,… … 依此类推,经过上述三层卷积之后输出再concat的结果与普通卷积的结果完全一致。

用pytorch的代码验证一下:
## slice卷积结果测试
inputs = torch.randn([1, 3, 224, 224])
weight1 = torch.randn([32, 3, 3, 3])
weight2 = torch.randn([64, 32, 3, 3])
weight3 = torch.randn([3, 64, 4, 4])
def conv2d(x, w1,w2,w3):
y1 = torch.nn.functional.conv2d(x, w1, stride=1, padding=1)
y2 = torch.nn.functional.conv2d(y1, w2, stride=2, padding=1)
y3 = torch.nn.functional.conv2d(y2, w3, stride=2, padding=1)
return y1
def conv2d_slice(x, w1,w2,w3):
pad1 = torch.nn.ZeroPad2d([1, 1, 1, 0])
pad2 = torch.nn.ZeroPad2d([1, 1, 0, 0])
pad3 = torch.nn.ZeroPad2d([1, 1, 0, 1])
x1 = x[:, :, 0:75, :]
x2 = x[:, :, 75-2:155, :]
x3 = x[:, :, 155-2:, :]
x1 = pad1(x1)
x2 = pad2(x2)
x3 = pad3(x3)
y1_1 = torch.nn.functional.conv2d(x1, w1, stride=1, padding=0)
y1_2 = torch.nn.functional.conv2d(x2, w1, stride=1, padding=0)
y1_3 = torch.nn.functional.conv2d(x3, w1, stride=1, padding=0)
y1_1_temp = y1_1[:, :, 0:74, :]
y1_1_slice = y1_1[:, :, 74-1:74, :]
y1_2_slice = y1_2[:, :, 80-1:80, :]
y1_2_overlap = torch.cat([y1_1_slice, y1_2], dim=2)
y1_3_overlap = torch.cat([y1_2_slice, y1_3], dim=2)
y1_1_temp = pad1(y1_1_temp)
y1_2_overlap = pad2(y1_2_overlap)
y1_3_overlap = pad3(y1_3_overlap)
y2_1 = torch.nn.functional.conv2d(y1_1_temp, w2, stride=2, padding=0)
y2_2 = torch.nn.functional.conv2d(y1_2_overlap, w2, stride=2, padding=0)
y2_3 = torch.nn.functional.conv2d(y1_3_overlap, w2, stride=2, padding=0)
y2_1_temp = y2_1[:, :, 0:37, :]
y2_1_slice = y2_1[:, :, 37-2:37, :]
y2_2_slice = y2_2[:, :, 40-2:40, :]
y2_2_overlap = torch.cat([y2_1_slice, y2_2], dim=2)
y2_3_overlap = torch.cat([y2_2_slice, y2_3], dim=2)
y2_1_temp = pad1(y2_1_temp)
y2_2_overlap = pad2(y2_2_overlap)
y2_3_overlap = pad3(y2_3_overlap)
y3_1 = torch.nn.functional.conv2d(y2_1_temp, w3, stride=2, padding=0)
y3_2 = torch.nn.functional.conv2d(y2_2_overlap, w3, stride=2, padding=0)
y3_3 = torch.nn.functional.conv2d(y2_3_overlap, w3, stride=2, padding=0)
y = torch.cat([y1_1, y1_2, y1_3], dim=2)
return y
out1 = conv2d(inputs, weight1, weight2, weight3)
out2 = conv2d_slice(inputs, weight1, weight2, weight3)
print(out1.shape)
print(out2.shape)
print(torch.allclose(out1, out2)) # 判断两个tensor是否相等
输出:
>>torch.Size([1, 32, 224, 224])
>>torch.Size([1, 32, 224, 224])
>>True
4、结论及加速效果
由上述示例可以看出,如果输入为[75,(2)+80,(2)+69],其中(2)表示从前面slice 2个像素点到后面,第一层卷积后的结果再将第一块slice一个像素给第二块,第二块slice一个像素给第三块,… … 依此类推,经过上述三层卷积之后输出再concat的结果与普通卷积的结果完全一致,也就是说利用这种slice卷积的思想,当卷积的输入太大时可以减少内存占用,同时加速卷积的计算。
经测试,在自研芯片上输入尺寸为[1,3,2224,2224],内存占用超过6MB时,普通卷积的帧率FPS为72,分三块slice卷积的帧率FPS为119,效率提升65.28%,加速效果明显!