二叉树的详解与常见算法实现
文章目录
-
- 一、 二叉树的基本概念
- 二、 二叉树的类型
- 1、满二叉树Full Binary Tree
- 2、完全二叉树Complete Binary Tree
- 3、平衡二叉树Balanced Binary Tree
- 4、二叉搜索树Binary Search Tree
- 5、红黑树Red Black Tree
- 三、二叉树的算法实现
- 1、结构体
- 2、二叉树的创建
- 3、按层创建二叉树
- 4、清除二叉树
- 5、前序遍历(根左右)递归方法
- 6、前序遍历非递归写法
- 7、中序遍历(左中右)
- 8、后序遍历(左右中)
- 9、层序遍历
- 10、求二叉树深度
- 11、二叉树节点总数目
- 12、返回叶子节点
- 13、建立二叉搜索树,左小右大
- 14、二叉搜索树查找
- 15、二叉搜索树删除
- 16、判断一颗树是否平衡二叉树
- 17、将二叉搜索树转换成一个排序的双向链表
- 18、判断是否为二叉树的子结构
- 19、判断是否为镜像
- 20、判断是否为完全二叉树
- 21、二叉树重建
一、 二叉树的基本概念
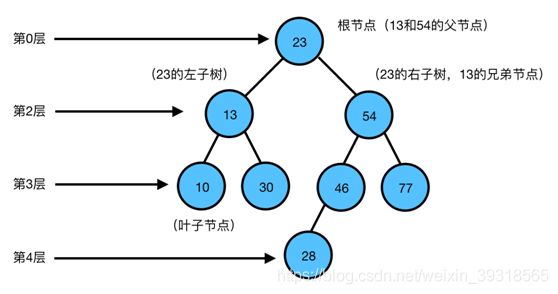
二叉树:二叉树是每个节点最多有两个子树的树结构。
根节点:一棵树最上面的节点称为根节点。
父节点、子节点:如果一个节点下面连接多个节点,那么该节点称为父节点,它下面的节点称为子 节点。
叶子节点:没有任何子节点的节点称为叶子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点。
节点度:节点拥有的子树数。上图中,13的度为2,46的度为1,28的度为0。
树的度:所有结点的度数的最大值。二叉树的度小于等于2。
树的深度:从根节点开始(其深度为0)自顶向下逐层累加的。上图中,13的深度是1,30的深度是2,28的深度是3。
树的高度:从叶子节点开始(其高度为0)自底向上逐层累加的。54的高度是2,根节点23的高度是3。对于树中相同深度的每个节点来说,它们的高度不一定相同,这取决于每个节点下面的叶子节点的深度。上图中,13和54的深度都是1,但是13的高度是1,54的高度是2。
二、 二叉树的类型
1、满二叉树Full Binary Tree
除最后一层无任何子节点外,每一层上的所有节点都有两个子节点,最后一层都是叶子节点。满足下列性质:
1)一颗树深度为h,最大层数为k,深度与最大层数相同,k=h;
2)叶子节点数(最后一层)为2^(k−1);
3)第 i 层的节点数是:2^(i−1);
4)总节点数是:2^k-1,且总节点数一定是奇数。
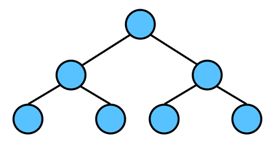
2、完全二叉树Complete Binary Tree
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。满足下列性质:
1)只允许最后一层有空缺结点且空缺在右边,即叶子节点只能在层次最大的两层上出现;
2)对任一节点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个;
3)除最后一层,第 i 层的节点数是:2^(i−1);
4)有n个节点的完全二叉树,其深度为:log2n+1或为log2n+1;
5)满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
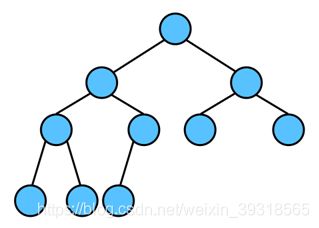
3、平衡二叉树Balanced Binary Tree
又被称为AVL树,它是一颗空树或左右两个子树的高度差的绝对值不超过 1,并且左右两个子树都是一棵平衡二叉树。

4、二叉搜索树Binary Search Tree
又称二叉查找树、二叉排序树(Binary Sort Tree)。它是一颗空树或是满足下列性质的二叉树:
1)若左子树不空,则左子树上所有节点的值均小于或等于它的根节点的值;
2)若右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
3)左、右子树也分别为二叉排序树。

5、红黑树Red Black Tree
是每个节点都带有颜色属性(颜色为红色或黑色)的自平衡二叉查找树,满足下列性质:
1)节点是红色或黑色;
2)根节点是黑色;
3)所有叶子节点都是黑色;
4)每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
5)从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

三、二叉树的算法实现
1、结构体
struct BTreeNode
{
int data;
BTreeNode * left;
BTreeNode * right;
};
2、二叉树的创建
void create(BTreeNode* & Node)
{
int data = 0;
cin>>data;
if(data > 0)
{
Node = new BTreeNode;
Node->data = data;
create(Node->left);
create(Node->right);
}
else
{
Node = NULL;
return;
}
}
3、按层创建二叉树
void levelCreate(BTreeNode* &Node)
{
queue<BTreeNode*> que;
int data;
cin>>data;
if(data > 0)
{
Node = new BTreeNode;
Node->data = data;
que.push(Node);
}
else
{
Node = NULL;
return;
}
while(!que.empty())
{
BTreeNode * node = que.front();
que.pop();
int data = 0;
cin>>data;
if(data > 0)
{
node->left = new BTreeNode;
node->left->data = data;
que.push(node->left);
}
else
{
node->left = NULL;
}
cin>>data;
if(data > 0)
{
node->right = new BTreeNode;
node->right->data = data;
que.push(node->right);
}
else
{
node->right = NULL;
}
}
}
4、清除二叉树
void clear(BTreeNode * & Node)
{
BTreeNode * p = Node;
if(p != NULL)
{
clear(Node->left);
clear(Node->right);
delete p;
}
}
5、前序遍历(根左右)递归方法
void preorderTree(BTreeNode * Node)
{
if(Node != NULL)
{
cout << Node->data << endl;
preorderTree(Node->left);
preorderTree(Node->right);
}
}
6、前序遍历非递归写法
void preorderTree1(BTreeNode* & Node)
{
stack<BTreeNode*> node;
node.push(Node);
BTreeNode * pNode = Node;
while(pNode != NULL && !node.empty())
{
if(pNode != NULL)
{
cout << pNode->data << endl;
node.push(Node);
pNode = Node->left;
}
else
{
BTreeNode * treeNode = node.top();
node.pop();
if(treeNode)
{
pNode = treeNode->right;
}
}
}
}
7、中序遍历(左中右)
void inorderTree(BTreeNode * Node)
{
if(Node == NULL)
{
return;
}
inorderTree(Node->left);
cout << Node->data << endl;
inorderTree(Node->right);
}
8、后序遍历(左右中)
void postorderTree(BTreeNode * Node)
{
if(Node != NULL)
{
return;
}
postorderTree(Node->left);
postorderTree(Node->right);
cout << Node->data << endl;
}
9、层序遍历
void levelTree(BTreeNode * Node)
{
queue<BTreeNode*> que;
if(Node == NULL)
{
return;
}
que.push(Node);
cout << Node->data << endl;
while(!que.empty())
{
BTreeNode * BtreeNode = que.front();
cout << BtreeNode->data << endl;
if(BtreeNode->left != NULL)
{
que.push(BtreeNode->left);
}
if(BtreeNode->right != NULL)
{
que.push(BtreeNode->right);
}
}
}
10、求二叉树深度
int depthofTree(BTreeNode * Node)
{
if(Node == NULL)
{
return 0;
}
return max(depthofTree(Node->left), depthofTree(Node->right)) + 1;
}
11、二叉树节点总数目
int getNodeNum(BTreeNode * Node)
{
if(Node == NULL)
{
return 0;
}
return getNodeNum(Node->left) + getNodeNum(Node->right) + 1;
}
12、返回叶子节点
int getLeafNum(BTreeNode * Node)
{
if(Node == NULL)
{
return 0;
}
if(Node->left == NULL && Node->right == NULL)
{
return 1;
}
return getLeafNum(Node->left) + getLeafNum(Node->right);
}
13、建立二叉搜索树,左小右大
bool insertTree(BTreeNode * Node, int data)
{
if(Node == NULL)
{
Node = new BTreeNode;
Node->data = data;
Node->left = NULL;
Node->right = NULL;
return true;
}
if(Node->data == data)
{
return false;
}
if(Node->data > data)
{
return insertTree(Node->left, data);
}
else
{
return insertTree(Node->right, data);
}
}
14、二叉搜索树查找
BTreeNode * SearchTree(BTreeNode * Node, int data)
{
if(Node == NULL)
{
return NULL;
}
if(Node->data == data)
{
return Node;
}
if(Node->data > data)
{
return SearchTree(Node->left, data);
}
else
{
return SearchTree(Node->right, data);
}
}
15、二叉搜索树删除
void deleteBTreeNode(BTreeNode* & Node, int data)
{
if(Node == NULL)
{
return;
}
if(Node->data == data)
{
if(Node->left == NULL)//这是左子树为空 如果是叶子节点也会在这里处理
{
BTreeNode * temp = Node;
Node = temp->right;
delete(Node);
}
else if(Node->right == NULL)//右子树为空的情况
{
BTreeNode * temp = Node;
Node = temp->left;
delete(temp);
}
else//左右子树都存在的情况稍微麻烦一些 对于删除这样的节点为了保持BST的性质
{
//我们要找到这个节点右侧的最小节点 或者 左侧的最大节点 这里用的是左侧最大节点
//要删除的节点的右侧节点
BTreeNode * temp = Node->right;
while(temp->left != NULL)
{
//一直找到最小的节点(根据BST的性质 最小节点一定会在最左侧的位置上)
temp = temp->left;
}
//覆盖之前节点的值
Node->data = temp->data;
//还要删除掉最小的那个节点 这个节点一定是在前面的情况(是叶子节点或者只有右子树)中 所以直接递归调用
deleteBTreeNode(Node->right, temp->data);
}
}
else if(Node->data > data)
{
deleteBTreeNode(Node->left, data);
}
else if(Node->data < data)
{
deleteBTreeNode(Node->right, data);
}
}
16、判断一颗树是否平衡二叉树
平衡二叉树的定义为:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1, 并且左右两个子树都是一棵平衡二叉树。
int maxDepthofTree(BTreeNode * Node)
{
if(Node == NULL)
{
return 0;
}
return max(maxDepthofTree(Node->left), maxDepthofTree(Node->right))+1;
}
bool isBalanced(BTreeNode * Node)
{
if(Node == NULL)
{
return true;
}
int left = maxDepthofTree(Node->left);
int right = maxDepthofTree(Node->right);
int diff = left - right;
if(diff > 1 || diff < -1)
{
return false;
}
return isBalanced(Node->left)&&isBalanced(Node->right);
}
17、将二叉搜索树转换成一个排序的双向链表
void ConvertNode(BTreeNode * Node, BTreeNode * &pListNode)
{
if(Node == NULL)
{
return;
}
BTreeNode * pCurrent = Node;
if(pCurrent->left != NULL)
{
ConvertNode(Node->left, pListNode);
}
pCurrent->left = pListNode;//当前二叉树节点左边指针指向链表
if(pListNode != NULL)
{
pListNode->right = pCurrent;//链表的右指针指向当前二叉树节点
}
pListNode = pCurrent;//始终指向链表中存在的最后一个元素。
if(pCurrent->right != NULL)
{
ConvertNode(Node->right, pListNode);
}
}
BTreeNode * Convert(BTreeNode * Node)
{
BTreeNode * pListNode = NULL;
ConvertNode(Node, pListNode);
BTreeNode * pHeadList = pListNode;
while(pHeadList != NULL && pHeadList->left != NULL)
{
pHeadList = pHeadList->left;//左边节点已经变为链表前驱通过前驱找到头节点
}
return pHeadList;
}
18、判断是否为二叉树的子结构
bool isSub(BTreeNode * Node, BTreeNode * SubNode)
{
if(SubNode == NULL)
{
return true;
}
if(Node == NULL)
{
return false;
}
if(Node->data != SubNode->data)
{
return false;
}
return isSub(Node->left, SubNode->left) && isSub(Node->left, SubNode->left);
}
//判断是否为二叉树的子结构
bool isSubStruct(BTreeNode * Node, BTreeNode * SubNode)
{
if(Node == NULL || SubNode == NULL)
{
return false;
}
bool result = false;
if(Node->data == SubNode->data)
{
result = isSub(Node, SubNode);
}
if(!result)
{
result = isSubStruct(Node->left, SubNode);
}
if(!result)
{
result = isSubStruct(Node->right, SubNode);
}
return result;
}
19、判断是否为镜像
bool isMirror(BTreeNode * NodeA, BTreeNode * NodeB)
{
if(NodeA == NULL && NodeB == NULL)
{
return true;
}
if(NodeA == NULL || NodeB == NULL)
{
return false;
}
if(NodeA->data != NodeB->data)
{
return false;
}
return isMirror(NodeA->left, NodeB->right) && isMirror(NodeA->right, NodeB->left);
}
20、判断是否为完全二叉树
某节点没有左孩子,则一定无右孩子
若某节点缺左或右孩子,则其所有后继一定无孩子
bool isCompleteTree(BTreeNode * Node)
{
if(Node == NULL)
{
return true;
}
int Tag = 0;
queue<BTreeNode*> que;
que.push(Node);
while(!que.empty())
{
BTreeNode * temp = que.front();
que.pop();
if(temp->left == NULL)
{
Tag = 1;//表示后面不能有节点了
}
else if(temp->left != NULL && Tag == 0)
{
que.push(temp->left);
}
else if(temp->left != NULL && Tag == 1)
{
return false;
}
if(temp->right == NULL)
{
Tag = 1;
}
else if(temp->right != NULL && Tag == 0)
{
que.push(temp->right);
}
else if(temp->right != NULL && Tag == 0)
{
return false;
}
}
}
21、二叉树重建
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树
BTreeNode * rebuildTree(int * pre, int * in, int len)
{
if(pre == NULL || in == NULL || len <= 0)
{
return NULL;
}
int i = 0;
int data = *pre;
BTreeNode * Node = new BTreeNode;
Node->data = data;
while(i<len && in[i] != data)
{
i++;
}
if(i==len)
{
return NULL;
}
Node->left = rebuildTree(pre+1, in, i);
Node->right = rebuildTree(pre+1+i, in+i+1, len-i-1);
return Node;
}