浮点数详解（一篇彻底学通浮点数）

浮点数

一.什么是浮点数

浮点数是与定点数相对的概念，计算机中的定点数约定小数点的位置不变，即人为约定俗成地规定了一个数小数点的位置。例如定点纯整数约定了小数点在数值位的最后。定点纯小数约定了数值位的最高位在小数点后面。

由于计算机字长的限制，当需要表示的数据有很大的数值范围时，他们不能直接用定点小数或者定点整数表示

二.浮点数的形式

浮点数由尾数M和阶码E构成。基数为2的数F的浮点数表示为：
$$F=M\ast 2^E$$

浮点数编码规则：

• 尾数M必须为小数，用n+1位有符号定点小数表示，可采用的原码，补码。阶码E必须为整数，用k+1位有符号定点整数表示，可采用原码，补码，移码。浮点数编码的位数m=(n+1)+(k+1)
• 浮点数的编码格式有多种，格式的选择可由计算机设计人员决定，例如：

阶符	阶码数值部分	数符	尾数数值部分
1	k	1	n

其中：

(1)阶码是整数，其位数k+1决定了浮点数表示的数值范围，也就是决定了数据的大小，或小数点在数据中的真实位置。阶符决定阶码的正负。即阶码越长，所能表示的范围越大

(2)尾数是小数，其位数n+1决定了浮点数的精度，如果尾数采用小数且位数n足够长，则当浮点数运算需要对尾数运算结果舍入时，造成的数据精度损失会比较小。即尾数越长，所能表示的精度越高

(3)尾数的符号表示浮点数的正负。

1.非规格化浮点数

当对尾数M只要求是小数而无其他限制时，此时的浮点数被称为非规格化浮点数。
假设阶码和尾数都用补码表示，则非规格化浮点数可表示的范围如下：

阶码和尾数	数值	阶码和尾数	数值
阶码最小值	$-2^k$	阶码最大值	$2^k-1$
尾数最小负值	-1	尾数最大负值	$-2^{-n}$
尾数最小正值	$+2^{-n}$	尾数最大正值	$+(1-2^{-n})$

以8位数值位，一位符号位的阶码为例子： 由于用补码表示，
所以阶码的最小值应该为：1 00000000 即 -2^8 = -256
而阶码的最大值应为：0 11111111 即 2^8-1 = 255

再来分析尾数的情况，假设尾数也是8位数值位，1为符号位补码的形式：
由于我们限定了浮点数的尾数只能是小数，所以我们当成定点纯小数的形式进行分析：
1.00000000表示了-1的补码，即尾数的最小负值
1.11111111 表示了 $-2^{-n}$的补码，即尾数的最大负值,其原码是1.00000001
0.11111111表示了$+(1-2^{-n})$的补码（原码），即尾数的最大正值
0.00000001表示了$+2^{-n}$的补码（原码），即尾数的最小正值
当然0.00000000表示0，是其最小绝对值

2.规格化浮点数

为了使有限字长的二进制尾数能表示更多的有效数位，同时使浮点数有统一的表示形式，浮点数通常采用规格化形式来表示。

规格化浮点数要求将尾数M的绝对值限定在规定的数值范围之内，即
$$\frac{1}{2}\le |M|<1（对于原码而言）$$

要使尾数的绝对值在此范围内，通过改变小数点的位置（相应地改变阶码）就可以做到。

为什么要这样做，我们举一个最简单的例子，假如一个尾数M用原码表示为：
0.00101000，那么这8位尾数的前2位都是0，这2个0实际上是无效数值位，我们完全可以改写成： $$0.101000xx\times 2^{-2}$$ 当1左移到最高位时，尾数后面多出来了两位可以多表示两个有效位来提高精度（尾数越长，浮点数精度越高）
例如同样要表示1101.1000000这个数，那么我们可以有这样的不唯二的两种表示形式：
$$（1）0.11011000\times 2^4$$
其中尾数是0 .11011101，阶码是0 0100
$$（2）0.00110110\times 2^6$$
其中尾数是0 .00110110，阶码是0 1100
(1)和(2)中，(1)是规格化浮点数，而(2)不是规格化浮点数

若尾数M用补码表示，
则当M$\ge$ 0时，规格化尾数的形式必须为：
$$[M{]}_{补}=0.1XXXXXXX$$
则当M< 0时，规格化尾数的形式必须为：
$$[M{]}_{补}=1.0XXXXXXX$$

其中X为任意二进制值

---

⭐注意（重点）⭐：

• 以上形式才是判断浮点数是否规格化的一般方法：看尾数补码的符号位与数值为最高位异或是否为1（即符号位与数值最高位不同）
• 判断浮点数是否规格化的根本思想是：尾数数值位首位必须以有效位开头
• 对于正数补码（原码）而言，有效位为1；对于负数补码而言，有效位为0
• 基于以上判定准则，尾数-1（补码）是规格化形式；尾数-1/2（补码）不是规格化形式，注意不要与原码规格化判定的绝对值范围混淆

三.IEEE754标准浮点数

1.单精度浮点数

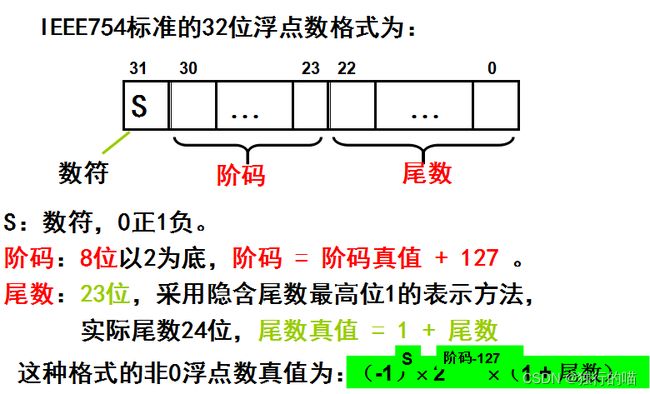
IEEE 754规定单精度浮点数的真值一般表示为：
$$N=(-1{)}^s\times 2^{e-127}\times 1.f$$

单精度浮点数编码格式由三个字段构成：

• 数符s为1位，表示浮点数的正负
• 尾数编码f为23位(采用原码表示)
• 阶码编码e为8位（含1位阶符，采用移码表示，偏移量127）

其中需要注意的是：
（1）IEEE 754中的阶码采用移码来表示，但对于单精度浮点数来说，移码的偏移量不是$2^7$而是$2^7-1=127$,这是因为IEEE 754将移码编码的全0和全1作为了特殊标识。

（2）IEEE 754浮点数是规格化浮点数，为了能够更多地表示尾数的有效数位，规定尾数真值的整数部分必须为1，尾数编码时整数1隐去，小数部分f用原码表示。

对于阶码e全0和全1时的特殊含义：

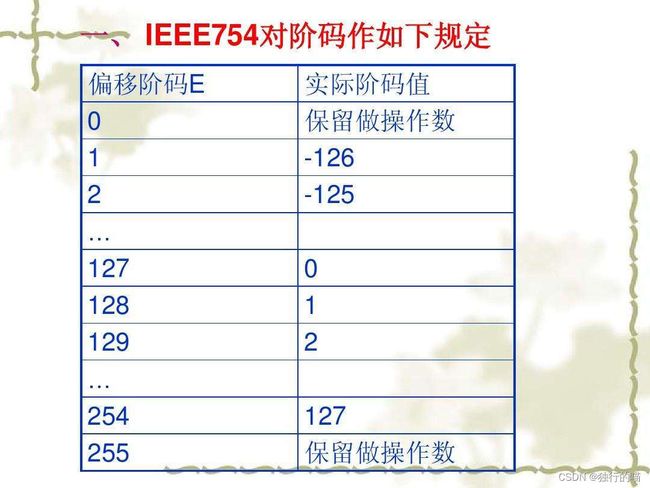
• (1)当阶码全0，且尾数f不全0时，表示该浮点数不是规格化浮点数，尾数实际为：
  $$0.XXXXXXXX（次正规数）$$
       \space \space \space\space     而不是规定形式的：
  $$1.XXXXXXXX$$
• (2)当阶码e全1，且尾数f全为0时，则该浮点数表示正无穷大或负无穷大，当数符s为1时，表示负无穷大，当数符s为0时，表示正无穷大。
• (3)当阶码e全1，且尾数f不全为0时，则该浮点数表示非数值数据（NaN）。

总结.对于单精度浮点数：
(1)阶码的真值E=e-127，并且0

(2)当e=0或255时，在IEEE 754中表示特殊的数。

(3)所能表示的范围为：
$$正数为：+2^{+127}\times (1+1-2^{-23})到+2^{-126}\times (1+0)$$
$$负数为：-2^{+127}\times (1+1-2^{-23})到-2^{-126}\times (1+0)$$

2.双精度浮点数

简要说明双精度浮点数（与单精度浮点数相类似）：

（1)阶码的真值E的取值范围为：-1022 ~ +1023,偏移量为+1023,阶码移码编码e为：
+1 ~ + 2046

（2）双精度浮点数的规格化数表示为：
$$N=(-1{)}^s\times 2^{e-1023}\times 1.f$$

（3）所能表示的规格化数范围：
$$正数为：+2^{+1023}\times (1+1-2^{-52})到+2^{-1022}\times (1+0)$$
$$负数为：-2^{+1023}\times (1+1-2^{-52})到-2^{-1022}\times (1+0)$$

（4）当e=0或e=2047时，在IEEE 754标准中表示特殊的数

浮点数的舍入规则：
1、就近舍入
2、朝0舍入
3、朝正无穷舍入
4、朝负无穷舍入
可以参考博文：IEEE754标准中的4种舍入规则

---

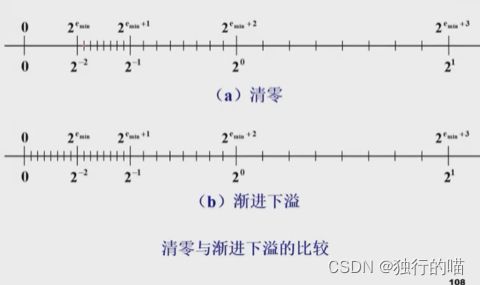
IEEE754浮点数的下溢

四.浮点数的运算

1.浮点数的加减法

假设有两个浮点数：
$$X=M_x\times 2^{E_x}$$
$$Y=M_y\times 2^{E_y}$$

• （1）对阶：尾数右移，小阶对大阶，阶码小的尾数右移，阶码+1
• （2）尾数加减法运算：使用补码运算，减法也采用补码加法实现
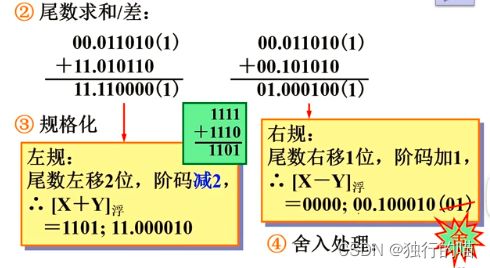
• （3）规格化：尾数加减法运算后，结果可能是非规格化数。如果结果的真值M不满足：$1/2\le M<1$,则是非规格化数需要规格化处理，根据情况分为以下两种处理方式：

运算结果尾数的规格化处理(左规）：

运算结果尾数的溢出处理(右规）：

• （4）舍入处理：尾数右移时将舍弃尾数最低位：1）截断法：直接将右移出的尾数低位丢弃。2）末位恒置1法：无论尾数右移丢弃的是1还是0，保证保留的尾数最低为永远为1。3）0舍1入法：规则如下图所示
  

浮点数加减法例题：

求解过程：

2.浮点数的乘除法

浮点数的乘法

浮点数的除法

浮点数规格化总结：

五.C语言中的浮点数分析

下面是一段c语言代码：

    float a = 12.5; 
    int *p =(int *) &a;
    int b=*p;
	  printf("b的值为：%d",b);

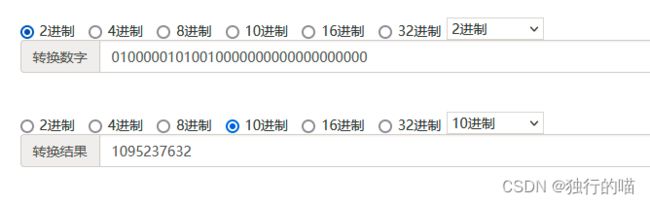
程序的执行结果是这样的：

我们来思考一下程序为什么会得出这样的结果，其实和IEEE 754单精度浮点数的存储规则密切相关：

学过c语言指针的同学不难看出，上面的代码不过是将单精度浮点数a 4个字节的存储空间中的所有数以整数int形式读出了而已。

下面我们根据IEEE 754单精度浮点数的规则，来推断12.5在4个字节的存储空间里是以怎样的二进制形式存放的。

IEEE 754单精度浮点数规定，1位数符，8位阶码（移码），23位尾数（原码）。
那么12.5的

• 数符s为：0

• 尾数为：10010000000000000000000（原码1.1001的小数部分：.1001）

• 阶码为：10000010（阶码真值为3，移码为：3+127=130）
  所以，整个32位的浮点数为：
  01000001010010000000000000000000
  将得到的二进制形式转换为10进制查看：
  
  转换之后与程序得出的结果一致，这就证明了C语言中float类型确实采用了IEEE 754单精度浮点数的标准。

• 补充内容：IEEE754浮点数的渐进下溢

• 补充内容：浮点数精度丢失分析