动图详解平衡树——平衡的二叉搜索树

更新于22.04.22

前言

本文参考了地哥的漫画图解平衡树，加了一些动图和自己的理解。

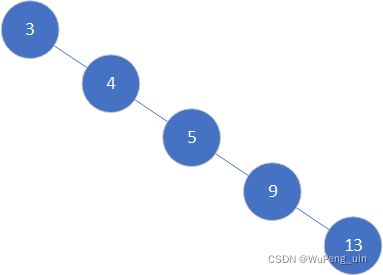
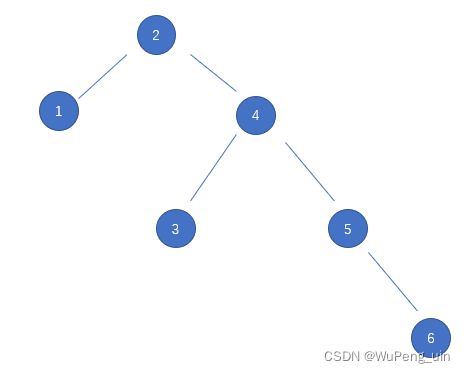
二叉搜索树可以借助二分的思想快速找到想要的元素，然而在最坏情况下，二叉搜索树会退化成下图这样的链表，导致查找性能大幅度下降。

看起来就像这样：

为了让树能够更平衡，AVL树，也就是平衡树被提出。

平衡树（AVL树）

平衡树是改进的二叉查找树，可以理解为“平衡的”二叉查找树，自然也具有二叉查找树所有的性质。

AVL树的AVL来自发明者的名字，本文统称为平衡树。

“平衡”的含义就在于：它可以平衡二叉查找树的高度，不会造成节点全在同一个方向一直延伸的情况，平衡树满足如下特性：

• 每个节点的左子树和右子树的高度差至多等于1。

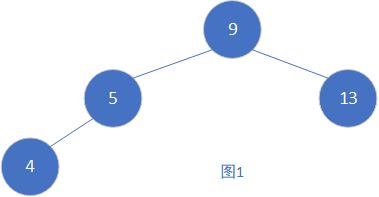
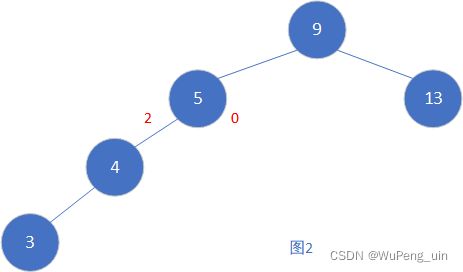
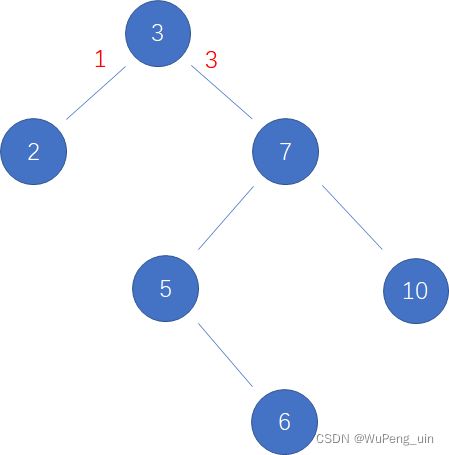
如下图图1就是平衡树，图2就是还没有平衡的二叉搜索树。

那么平衡树是怎么做到平衡的呢？

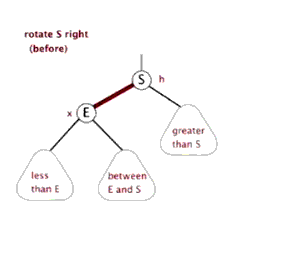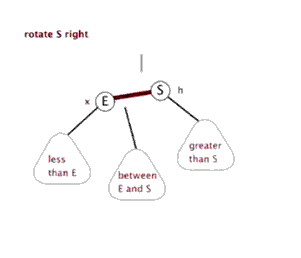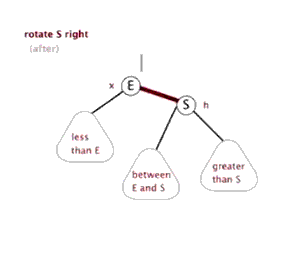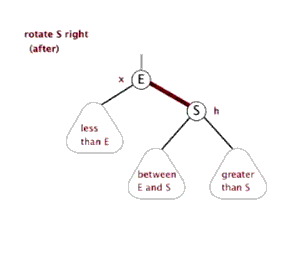
我们以刚才的图二为例，插入节点3时，发现高度差值大于1，搜索树“不平衡”了。现在给你高度的自由，不需要你写什么代码，你会怎么调整当前的结构让现在的树再变成平衡树？

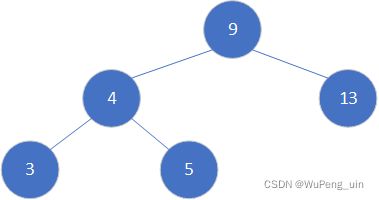
那就调整一下节点位置呗，这样现在的树还符合查找树的特点，同时也平衡了。

这种操作有个专门的术语：右旋，上面的结果可以由图2右旋节点5做到。有右旋，自然存在左旋，下面是两张动图，看起来是不是很像“平衡”的过程，我理解这也是平衡树的一个核心。

左旋和右旋

下面详细讲讲左旋和右旋。

左旋——右右型

在插入一个新节点时，可能出现所有节点都偏向右边的情况，比如下图新插入节点为6：

这时节点2的左子树高度为1，右子树高度为3，差值大于1，且插入的新节点的值（6）比当前不平衡节点的右子树（4）值大，即插入节点是向需要平衡节点的右孩子的右子树插入。

这种情况我们之称为右右型。这种情况下需要进行左旋，让树变得平衡：

可以对照下面这张动图，小于2的节点和大于4的节点都不需要变动相对位置，但是左旋以后，2、4中间的子树，需要变动为2的右子树。

左旋——右左型

已经讲过左旋为什么要再说一种？为什么右左型需要额外的处理？

我们还是以实例说明：

插入节点6，使得节点3失衡，且插入的新节点的值（6）比当前不平衡节点的右子树（7）值小，即插入节点是向需要平衡节点的右孩子的左子树插入。

这种情况我们称之为右左型。

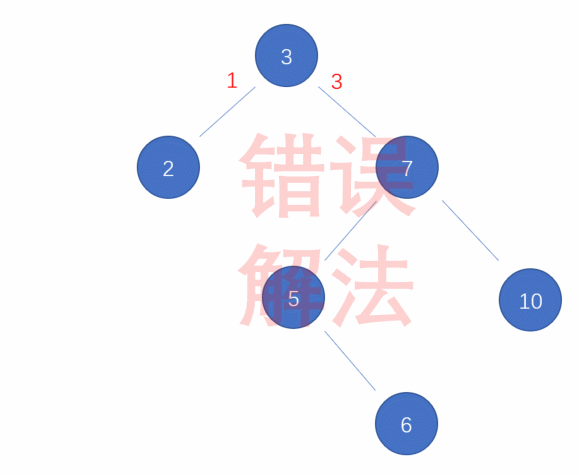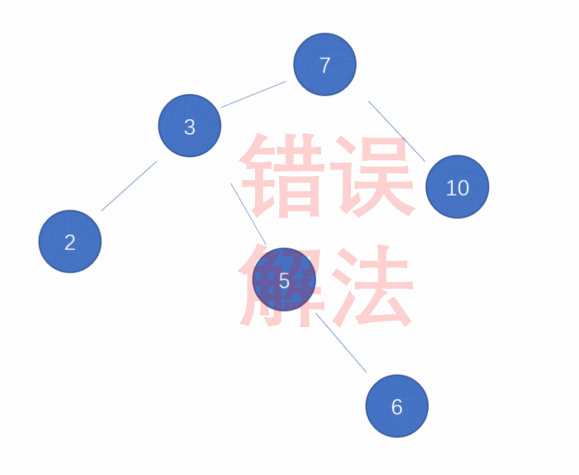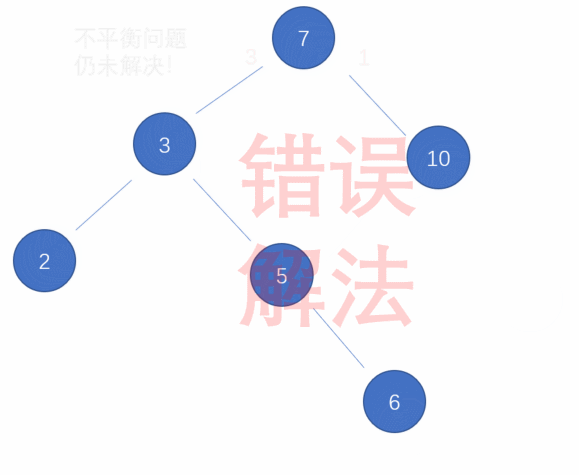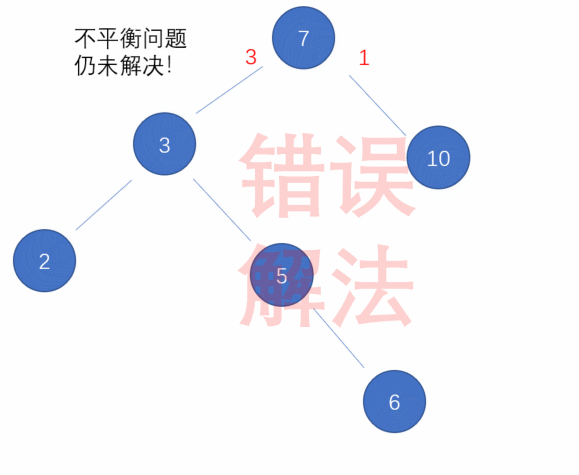
你可能会问：我直接套右右型的操作不行吗？那么我们试试看：

原因就出在3的右子树7上，插入6对于节点7来说虽然并没有违背平衡，但按照右右型处理后可能会造成新的失衡，所以我们要先对节点7，也就是失衡节点3的右孩子进行右旋，再按照右右型的操作对节点3进行左旋：

右旋同理

左左型和左右型镜像一下操作就可以得到，不多说。

一个样例

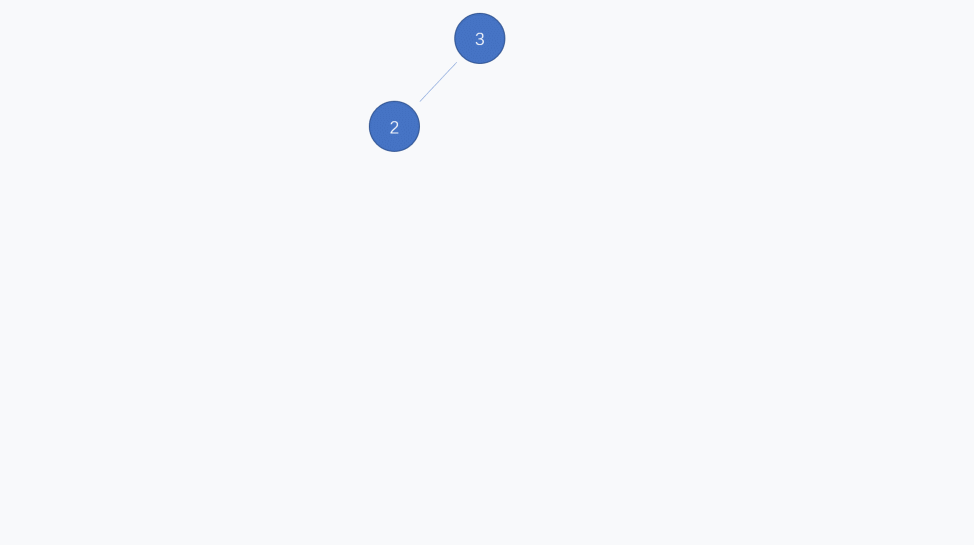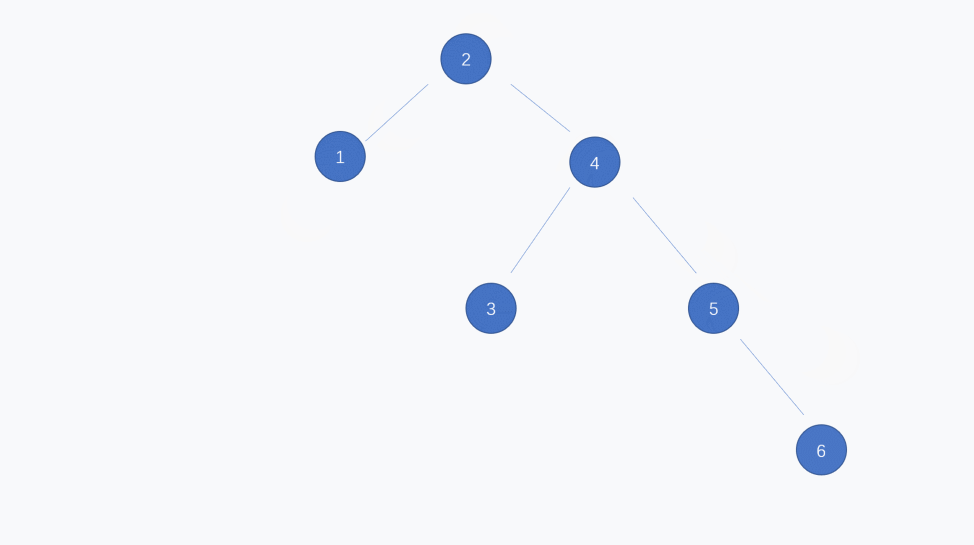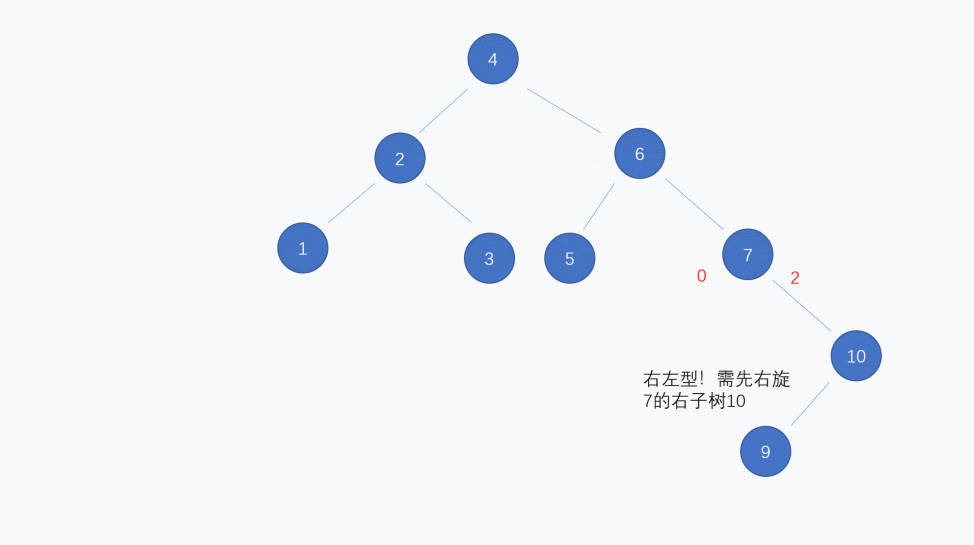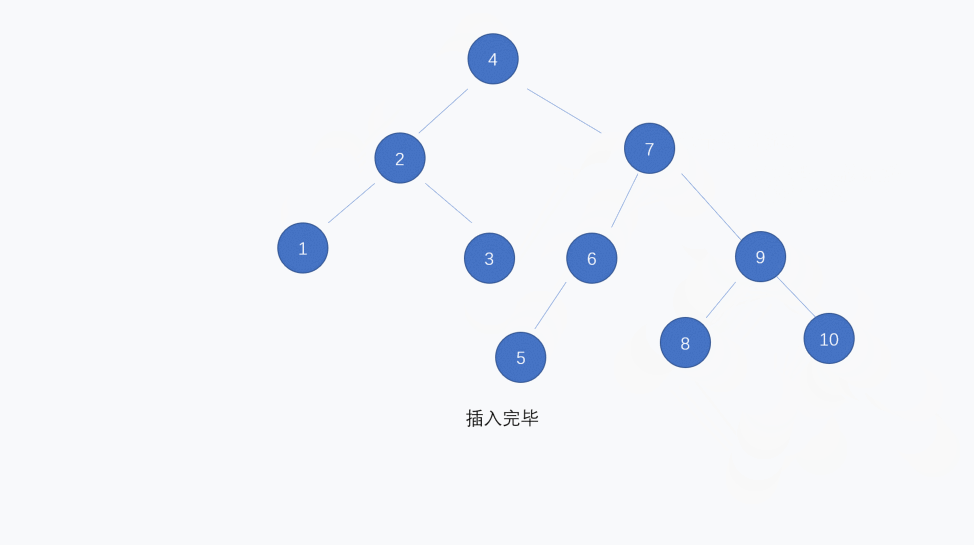
这里有动图例子，可以涵盖基本所有情况：二叉搜索树初始为3,2，我们依次插入：1,4,5,6,7,10,9,8：

总结

平衡树是为了将二叉搜索树进行“高度的平衡”，通过左旋、右旋等操作，使得左右节点的高度差小于等于1，从而保证了搜索树不会退化为链表。

代码实现（C++）

最好自己敲一遍，能更加熟悉和发现自己理解的BUG。

#include 

using namespace std;

struct AvlTreeNode {
    int val;
    AvlTreeNode *left;
    AvlTreeNode *right;
    int height;

    AvlTreeNode() : val(0), left(nullptr), right(nullptr), height(0) {}

    AvlTreeNode(int val_) : val(val_), left(nullptr), right(nullptr), height(0) {}

//    AvlTreeNode(int val_, AvlTreeNode *left_, AvlTreeNode *right_) : val(val_), left(left_), right(right_) {}
};

class AvlTree {
private:
    bool exists; // 待插入值已存在的标志
    static int height(AvlTreeNode *node) {
        if (node == nullptr) return -1;
        else return node->height;
    }

    // 左左型，右旋操作
    static AvlTreeNode *R_Rotate(AvlTreeNode *node2) {
        AvlTreeNode *node1;

        //进行旋转
        node1 = node2->left;
        node2->left = node1->right;
        node1->right = node2;

        //重新计算节点的高度
        node2->height = max(height(node2->left), height(node2->right)) + 1;
        node1->height = max(height(node1->left), height(node1->right)) + 1;

        return node1;
    }

    // 右右型，左旋操作
    static AvlTreeNode *L_Rotate(AvlTreeNode *node2) {
        AvlTreeNode *node1;

        //进行旋转
        node1 = node2->right;
        node2->right = node1->left;
        node1->left = node2;

        //重新计算节点的高度
        node2->height = max(height(node2->left), height(node2->right)) + 1;
        node1->height = max(height(node1->left), height(node1->right)) + 1;

        return node1;
    }

    // 右-左型，先对右子树进行右旋，再左旋
    static AvlTreeNode *R_L_Rotate(AvlTreeNode *node3) {
        // 先对其右孩子进行右旋
        node3->right = R_Rotate(node3->right);
        // 再进行左旋
        return L_Rotate(node3);
    }

    // 左-右型，先对左子树进行左旋，再右旋
    static AvlTreeNode *L_R_Rotate(AvlTreeNode *node3) {
        // 先对其孩子进行左旋
        node3->left = L_Rotate(node3->left);
        // 再进行右旋
        return R_Rotate(node3);
    }

    AvlTreeNode *insertRecursion(int value, AvlTreeNode *root) {
        if (root == nullptr) { // 找到应该插入的空节点位置，new一个节点插入
            root = new AvlTreeNode(value);
        } else if (value < root->val) { // 待插入值小于当前root的值，向其左子树递归插入
            root->left = insertRecursion(value, root->left);
            //进行调整操作
            //如果左孩子的高度比右孩子大2
            if (height(root->left) - height(root->right) == 2) {
                if (value < root->left->val) { //左-左型
                    root = R_Rotate(root);
                } else { //左-右型
                    root = R_L_Rotate(root);
                }
            }
        } else if (value > root->val) { // 待插入值小于当前root的值，向其左子树递归插入
            root->right = insertRecursion(value, root->right);
            // 进行调整
            // 右孩子比左孩子高度大2
            if (height(root->right) - height(root->left) == 2) {
                if (value > root->right->val) { // 右-右型
                    root = L_Rotate(root);
                } else { // 右-左型
                    root = R_L_Rotate(root);
                }
            }
        } else { // 否则，这个节点已经在Avl树上存在了
            this->exists = true;
        }


        //重新计算root的高度
        root->height = max(height(root->left), height(root->right)) + 1;
        return root;
    }


public:
    AvlTreeNode *pRoot;

    // 向树中插入值为value的节点，插入成功返回true，节点已存在则返回false
    bool insert(int value) {
        this->pRoot = insertRecursion(value, this->pRoot);
        if (this->exists) {
            this->exists = false;
            return false;
        } else {
            return true;
        }
    }

    AvlTree() : pRoot(nullptr), exists(false) {}

};


int main() {
    AvlTree Tree;
    Tree.insert(3);
    Tree.insert(2);
    Tree.insert(1);
    Tree.insert(4);
    Tree.insert(5);
    Tree.insert(6);
    Tree.insert(7);
    Tree.insert(10);
    Tree.insert(9);
    Tree.insert(8);

    return 0;
}