图的企业应用-A*算法自动寻路

引言

MC想必大家都玩过,但鸡哥利用A*自动寻路算法来找箱子 箱子里有鸡你太美唱片，和准备好的篮球
当然在这是游戏中找到的宝箱 还得原石x5等一大堆的养成物品 ???等等 ,原神 玩家露出鸡脚了吧! 不应该是 有鸡你太美唱片,还有一条鱼并且给梅里猫的名叫荔枝的? 这梅里猫 :说这一句话:“告诉,老默 我想吃鱼”,另一种猫叫:芝士猫"好,干 到沈阳没你好果子吃啊 " 突然一只名叫嘎子的人正在为狗子卖到缅北噶腰子 这只狗不听话:曾经是脚盆鸡的特派员 专门搞种花家的人民 于是种花家的人民军队 非常愤怒,更加愤怒的是那些没有一点察觉到危险性,
某泰民用灰机局,公然歧视兔子带来的人民,好家伙 紫荆花地区区长非常失望,…
那么怎么自动寻路? 那怎么到达这个地点 并且拿出 这么多的信息 当然最重要是鸡你太美唱片,篮球 还有那只梅里猫-荔枝

算法原理

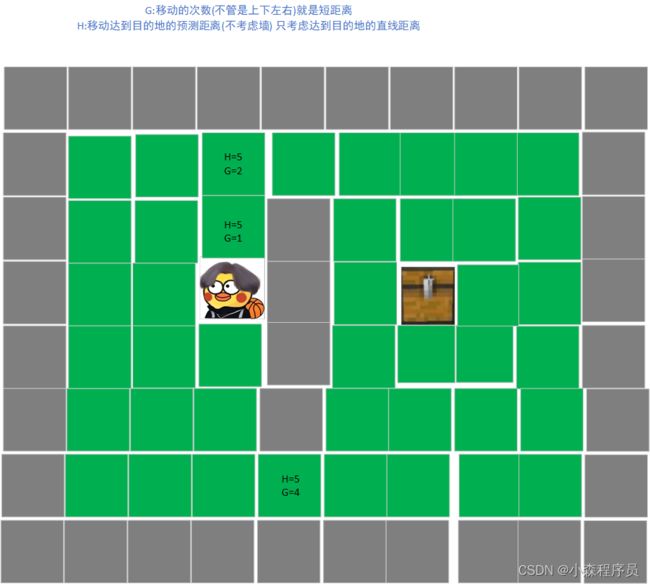
为了便于鸡哥自动寻路,那么我们可以简化为网格形状如下图所示

现在鸡哥正在急着找到 他的唱片 <鸡你太美和他的"原神原石还有养成物品,那只梅里猫的毛茸茸的玩具:名叫荔枝">
怎么办呢 emmmm 想着想着,还是靠场外的 网络ikun 疯狂打call 说"蔡徐坤"问题是在这里只有获得宝箱的才能,给手机,发维搏
其实这群网络真Ikun们一直等着我们家giegie出来发微博,…

突然想到了什么 我居然无法看终点在哪里,试着上下左右方向找 并且记录着当前走过 路径,走着走着就 发现可以预测需要走多少不才能终点 那我就不客气啦

经过计算 后

G:移动的次数(不管是上下左右)就是短距离
H:移动达到目的地的预测距离(不考虑墙) 只考虑达到目的地的直线距离
坤坤借着这个机会好好的恶补了下数学 突然开窍咯!
但坤坤发现没法弄呀的,大量的计算才行,于是乎陷入了迷茫之中 …
突然后背一个人 这个人不用多说:“是作者本人” 请问:“你需要技术支持吗”
技术支持? 对呀 其实对于这个简单的 也不简单 ,说他简单是因为二维数组 相当于数学的矩阵 数学那套还是挺管用的 ,但没有计算机怎么的算力 我可以帮你解决事情 但别再让你粉丝买流量 否则技术,让你难堪,你懂的
是技术帮你维护 每一个热搜 没了技术哪来的这个平台 你说是不是呀

“对对对”,技术是我的救命恩人 …

首先从上标粗的这段话很好理解一下,然后每一个方格对应的是元素 名叫地图元素 也就是所说的二维数组元素
只是大部分方格包含 地图坐标系x,y G ,H

假设坤坤在这个地方

G:移动的次数(不管是上下左右)就是短距离
H:移动达到目的地的预测距离(不考虑墙) 只考虑达到目的地的直线距离
坤坤可能觉得 往右走好一些 坤坤往右走一步 G=1 ,H=5 坤坤再往上走一步 G=2 ,H=5 坤坤再往上走一步 G=3 ,H=5
那这个F是是什么意思呢

G:移动的次数(不管是上下左右)就是短距离
H:移动达到目的地的预测距离(不考虑墙) 只考虑达到目的地的直线距离
F:总经过的路程 =H+G

• 核心思路:

1. 将起点加入open列表,起点的g值(实际花费)和h值(启发式评估值)初始化为0,起点的父节点设置为null。
2. 从open列表中选择f值(g值+h值,衡量路径承诺程度)最小的节点。这个节点的f值越小,表示该节点越有可能是最短路径的一部分。
3. 将选择出的节点从open列表移到closed列表。
4. 如果选择出的节点是目标节点,则构建路径并结束。else继续下一步。
5. 扩展当前选择出的节点,得到其相邻节点。
6. 对于每个相邻节点,如果在closed列表中则忽略,否则进行如下操作:

• 计算相邻节点的g值(等于父节点的g值+移动到相邻节点的代价)
• 计算相邻节点的h值(使用启发式函数)
• 计算相邻节点的f值(g值+h值)
• 如果相邻节点在open列表中,并且新的g值更小,则更新相邻节点的g值、f值和父节点
• 否则,将相邻节点添加到open列表,并设置相邻节点的父节点、g值和f值

7. 重复2-6步,直到找到目标节点position。
8. 通过追踪父节点,从目标节点position反向构建最短路径。
9. 返回最短路径。

A*算法实现

A*算法声明

#ifndef __ASTAR_H__
#define __ASTAR_H__

#include

using std::list;

//AI寻路地图
struct AIPathMap {
	int* map;
	int Rows;
	int Cols;
};

//AI寻路地图道具
enum AIPathMapItem {
	//墙
	Wall,

	//地面
	Ground,

	//坤坤
	KunKun,

	//箱子
	Box

};

// AIpoint 结构体，表示二维平面上的点    
struct AIpoint {
	int x; // x坐标    
	int y; // y坐标    
};

// AIPathStrategy 结构体，表示到达点的路径策略  
struct AIPathStrategy {
	int G; // 移动的次数（上下左右都算一次短距离）  
	int H; // 移动达到目的地的预测距离（不考虑墙，只考虑直线距离）  
	int F; // 总经过的路程（H + G）  
};

// AIGrid 结构体，表示二维平面上的网格，包含一个点和一个路径策略    
struct AIGrid {
	AIpoint point; // 点结构体    
	AIPathStrategy PathStrategy; // 路径策略结构体    
	AIGrid* Parent; // 指向父网格的指针    
};

//直移一格 消耗
const int MoveStraightOneSpace = 10;
//斜移一格 消耗
const int MoveSidewaysOneSpace = 14;

//初始化AI寻路地图
void InitAIPathMap(int *map,int Rows,int Cols);

//接收两个整数参数，分别表示点的 x 和 y 坐标，返回一个新的 AIpoint 结构体，表示该点。
AIpoint CreatorAAIpoint(int x, int  y);

//接收两个 AIpoint 类型的引用参数，表示起点和终点，返回一个包含 AIGrid 结构体的链表，表示从起点到终点自动寻找路径的结果。
list<AIGrid*> AStarAutoPath(AIpoint &start, AIpoint &end);

//创建全局资源
void CreatorGlobalResource();

//释放全局资源
void ReleaseGlobalResources();

#endif // !__ASTAR_H__

A*算法实现

#include "AStar.h"
#include
#include
#include
#include
using namespace std;

//A*自动寻路策略
struct AStarAutoPathStrategy{
	AIPathMap Map;
	list<AIGrid*> OpenList;
	list<AIGrid*> CloseList;
};

static  AStarAutoPathStrategy  *AStarAutoPaths;

void InitAIPathMap(int* map, int Rows, int Cols){

	AStarAutoPaths->Map.map = map;
	AStarAutoPaths->Map.Rows = Rows;
	AStarAutoPaths->Map.Cols = Cols;
}

AIGrid* CreatorAIGrid(AIpoint & point){

	AIGrid* Grid = new AIGrid;
	*Grid = {};
	Grid->point = point;
	return Grid;
}


AIpoint CreatorAAIpoint(int x, int y)
{
	return { x,y };
}


//获取最小的F值方格
static AIGrid* GetGridlestFValue() {

	list<AIGrid*>& OpenList = AStarAutoPaths->OpenList;

	if (!OpenList.empty()) {
		auto resGrid = OpenList.front();
		auto iter = OpenList.begin();
		const auto iterEnd = OpenList.end();

		while (iter != iterEnd) {
						
			if (*iter) {
				auto& GridPathStrategy= (*iter)->PathStrategy;
				auto& resGridPathStrategy = resGrid->PathStrategy;

				if (GridPathStrategy.F < resGridPathStrategy.F){
					resGridPathStrategy = GridPathStrategy;
				}
			}
			++iter;
		}

		return resGrid;
	}

	return nullptr;

}

//判断开放/关列表中是否有目标方格
static AIGrid* isInList(list<AIGrid*> List, const AIGrid* targetGrid) {

	auto iter = List.begin();
	const auto iterEnd = List.end();
	const AIpoint& targetGridPoint = targetGrid->point;
	
	
	while (iter != iterEnd) {
		AIGrid* &Grid = *iter;
		const AIpoint& GridPoint = Grid->point;

		if (GridPoint.x == targetGridPoint.x && GridPoint.y == targetGridPoint.y){
			return Grid;
		}
		++iter;
	}

	return nullptr;

}

//是否相邻
static bool isAdj(const AIpoint& GridPoint, const AIpoint& targetGridPoint) {
	return (abs(GridPoint.x - targetGridPoint.x) + abs(GridPoint.y - targetGridPoint.y)) == 1;
}




//判断这个点是否存在于地图中
bool IsInMap(const AIPathMap& map, const AIpoint& GridPoint) {

	static const  int Rows = (AStarAutoPaths->Map.Rows - 1);

	static const  int Cols = (AStarAutoPaths->Map.Cols - 1);

	return GridPoint.x < 0 || GridPoint.x >(Rows) || GridPoint.y < 0 || GridPoint.y >(Cols);
}

//判断两个坐标是否相同
bool IsSamePoint(const AIpoint& p1, const AIpoint& p2) {
	return p1.x == p2.x && p1.y == p2.y;
}

//判断地图中是否存在满足条件的方格
bool HasGridMeetCondition(const AIPathMap& Map, const AIpoint& GridPointint, int type1, int type2) {
	return   (Map.map[GridPointint.x * Map.Cols + GridPointint.y] == type1 || Map.map[GridPointint.x * Map.Cols + GridPointint.y] == type2);
}

//判断是否可达到方格
static bool IsReachGrid(const AIGrid* Grid, const AIGrid* targetGrid) {

	AIPathMap& Map = AStarAutoPaths->Map;

	auto& PathMap = Map.map;
	const AIpoint& GridPoint = Grid->point;
	const AIpoint& targetGridPoint = targetGrid->point;

	if ((IsInMap(Map, targetGridPoint) || (HasGridMeetCondition(Map, targetGridPoint, Ground, Box) || IsSamePoint(GridPoint, targetGridPoint)) || isInList(AStarAutoPaths->CloseList, targetGrid))) {
		return false;
	}
	return isAdj(GridPoint, targetGridPoint);
}

//找到当前的方格认为最优的方格 并计算F值的
vector<AIGrid*> GetrimGrid(const AIGrid *Grid) {

	vector<AIGrid*> result;
	if (Grid){
		const int& AIpointX = Grid->point.x;
		const int& AIpointY = Grid->point.y;

		for (int x = AIpointX-1; x <= AIpointX+1; x++)	{

			for (int y = AIpointY-1; y <=AIpointY+1; y++){

				auto newPoint = CreatorAAIpoint(x, y);
				unique_ptr<AIGrid> newGridPtr(CreatorAIGrid(newPoint));
				auto &&newGrid = newGridPtr.get();

				if (IsReachGrid(Grid, newGrid)){
					result.push_back(newGridPtr.release());
				}
			}
		}

	}
	return result;

}

//计算寻路策略G值
static int CalculatePathStrategyGvalue(AIGrid* AIGridFirst, AIGrid* AIGridSecond) {
	
	const AIpoint& GridPoint = AIGridFirst->point; 
	const AIpoint& targetGridPoint = AIGridSecond->point;

	AIGrid* AIGridFirstParent = AIGridFirst->Parent;

	int* AIGridFirstParentGvakueByPtr = nullptr;

	if (AIGridFirstParent)	{
		AIGridFirstParentGvakueByPtr = &AIGridFirstParent->PathStrategy.G;
	}

	int CurrentTwoAIGridGvalue = isAdj(GridPoint, targetGridPoint) ? MoveStraightOneSpace : MoveSidewaysOneSpace;

	int AIGridFirstParentGvalue = AIGridFirstParentGvakueByPtr ? *AIGridFirstParentGvakueByPtr : 0;

	return CurrentTwoAIGridGvalue + AIGridFirstParentGvalue;

}

//计算寻路策略H值
static int CalculatePathStrategyHvalue(AIGrid* AIGridFirst, AIGrid* AIGridSecond) {

	const AIpoint& GridPoint = AIGridFirst->point;
	const AIpoint& EndtGridPoint = AIGridSecond->point;

	int result((int )sqrt(((double)(EndtGridPoint.x - GridPoint.x) * (double)(EndtGridPoint.x - (GridPoint.x))) + ((double)(EndtGridPoint.y - GridPoint.y) * (double)(EndtGridPoint.y - GridPoint.y)) * MoveStraightOneSpace));

	return result;
}

//计算寻路策略F值
static  int CalculatePathStrategyFValue(AIGrid* AIGridFirst) {

	return AIGridFirst->PathStrategy.G + AIGridFirst->PathStrategy.H;
}

//自动搜索路径
static AIGrid* AutoSearchPath(AIpoint& start, AIpoint& end) {


	AIGrid* StartGrid = CreatorAIGrid(start);
	unique_ptr<AIGrid> EndGrid(CreatorAIGrid(end));

	list<AIGrid*>& OpenList = AStarAutoPaths->OpenList;
	list<AIGrid*>& CloseList = AStarAutoPaths->CloseList;
	OpenList.push_back(StartGrid);

	AIGrid* resultGrid = nullptr;

	while (!OpenList.empty()) {

		//第一步从开放列表中取最小的F值的方格

		//获取最小的F值方格
		auto CurrentGrid = GetGridlestFValue();

		//第二步 :把当前的方格放入关闭列表中
		OpenList.remove(CurrentGrid);
		CloseList.push_back(CurrentGrid);

		//第三步 :找到当前的方格认为最优的方格 并计算F值的
		auto GridVector = GetrimGrid(CurrentGrid);

		for (auto& Grid : GridVector) {

			//对某一个方格，如果它不在开放列表中，加入到开启列表，设置	当前格为其父节点，计算 F G H
			AIGrid* exist = isInList(OpenList, Grid);
			AIPathStrategy* GridPathStrategy = &Grid->PathStrategy;
			if (!exist) {
				Grid->Parent = CurrentGrid;

				GridPathStrategy->G = CalculatePathStrategyGvalue(CurrentGrid, Grid);
				GridPathStrategy->H = CalculatePathStrategyHvalue(Grid, EndGrid.get());
				GridPathStrategy->F = CalculatePathStrategyFValue(Grid);

				OpenList.push_back(Grid);
			}
			else {
				int Gvalue = CalculatePathStrategyGvalue(CurrentGrid, Grid);

				if (Gvalue < GridPathStrategy->G) {
					exist->Parent = CurrentGrid;
					GridPathStrategy->G = Gvalue;
					GridPathStrategy = &exist->PathStrategy;
					GridPathStrategy->F = CalculatePathStrategyFValue(Grid);
				}
				
				delete Grid;
				Grid = nullptr;
				
			}
		}

		GridVector.clear();

		resultGrid = isInList(OpenList, EndGrid.get());
		if (resultGrid) {
			return 	 resultGrid;
		}
	}
	return 	 resultGrid;
	
}

list<AIGrid*> AStarAutoPath(AIpoint& start, AIpoint& end) {

	list<AIGrid*> result;

	//自动搜索路径
	auto resultPath = AutoSearchPath(start, end);

	while (resultPath)	{
		result.emplace_front(resultPath);
		resultPath = resultPath->Parent;
	}

	return result;

}


void CreatorGlobalResource(){
	
	AStarAutoPaths = new AStarAutoPathStrategy;
	AStarAutoPaths->CloseList.clear();
	AStarAutoPaths->OpenList.clear();
	AStarAutoPaths->Map = {};
}
void ReleaseGlobalResources(){

	list<AIGrid*>& OpenList = AStarAutoPaths->OpenList;
	list<AIGrid*>& CloseList = AStarAutoPaths->CloseList;

	auto iterEnd = CloseList.end();
	
	for (auto iter = CloseList.begin(); iter!=iterEnd;){

		delete* iter;
		iter = CloseList.erase(iter);
	}

	iterEnd = OpenList.end();

	for (auto iter = OpenList.begin(); iter != iterEnd;) {

		delete* iter;
		iter = OpenList.erase(iter);
	}

	delete AStarAutoPaths;
	AStarAutoPaths = nullptr;
}

这是bug

//判断是否可达到方格
static bool IsReachGrid(const AIGrid* Grid, const AIGrid* targetGrid) {

	AIPathMap& Map = AStarAutoPaths->Map;

	auto& PathMap = Map.map;
	const AIpoint& GridPoint = Grid->point;
	const AIpoint& targetGridPoint = targetGrid->point;

	if ((IsInMap(Map, targetGridPoint) || (HasGridMeetCondition(Map, targetGridPoint, Ground, Box) || IsSamePoint(GridPoint, targetGridPoint)) || isInList(AStarAutoPaths->CloseList, targetGrid))) {
		return false;
	}
	return isAdj(GridPoint, targetGridPoint);
}

不,来看一下输出

         0 0 0 0 0 0 0 0 0 0 0 0 0 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 3 1 1 1 0
         0 1 1 1 2 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 0 0 0 0 0 0 0 0 0 0 0 0 0

        坤坤:   方格坐标  x =5   方格坐标 y =4  到      宝箱:   方格坐标  x =4   方格坐标 y =9

解决方案:

//判断是否可达到方格
static bool IsReachGrid(const AIGrid* Grid, const AIGrid* targetGrid) {

	AIPathMap& Map = AStarAutoPaths->Map;

	auto& PathMap = Map.map;
	const AIpoint& GridPoint = Grid->point;
	const AIpoint& targetGridPoint = targetGrid->point;

	if ((IsInMap(Map, targetGridPoint) || (HasGridMeetCondition(Map, targetGridPoint, Ground, Box) && IsSamePoint(GridPoint, targetGridPoint)) || isInList(AStarAutoPaths->CloseList, targetGrid))) {
		return false;
	}
	return isAdj(GridPoint, targetGridPoint);
}

如果你觉得这样就结束了
不,来看一下输出

         0 0 0 0 0 0 0 0 0 0 0 0 0 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 3 1 1 1 0
         0 1 1 1 2 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 0 0 0 0 0 0 0 0 0 0 0 0 0

        坤坤:   方格坐标  x =5   方格坐标 y =4  到      宝箱:   方格坐标  x =4   方格坐标 y =9

第二个 bug

//判断是否可达到方格
static bool IsReachGrid(const AIGrid* Grid, const AIGrid* targetGrid) {

	AIPathMap& Map = AStarAutoPaths->Map;

	auto& PathMap = Map.map;
	const AIpoint& GridPoint = Grid->point;
	const AIpoint& targetGridPoint = targetGrid->point;

	if ((IsInMap(Map, targetGridPoint) || (HasGridMeetCondition(Map, targetGridPoint, Ground, Box) && IsSamePoint(GridPoint, targetGridPoint)) || isInList(AStarAutoPaths->CloseList, targetGrid))) {
		return false;
	}
	return isAdj(GridPoint, targetGridPoint);

         0 0 0 0 0 0 0 0 0 0 0 0 0 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 2 1 1 0 1 3 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 0 0 0 0 0 0 0 0 0 0 0 0 0

        坤坤:   方格坐标  x =4   方格坐标 y =4  到      宝箱:   方格坐标  x =4   方格坐标 y =9
        方格坐标  x =4   方格坐标 y =4  方格策略 G =0   方格策略H =0    方格策略F =0
        方格坐标  x =4   方格坐标 y =5  方格策略 G =10  方格策略H =12   方格策略F =22
        方格坐标  x =4   方格坐标 y =6  方格策略 G =10  方格策略H =9    方格策略F =19
        方格坐标  x =4   方格坐标 y =7  方格策略 G =20  方格策略H =6    方格策略F =26
        方格坐标  x =4   方格坐标 y =8  方格策略 G =20  方格策略H =3    方格策略F =23
        方格坐标  x =4   方格坐标 y =9  方格策略 G =30  方格策略H =0    方格策略F =30

虽然输出结果了但还是有点不对劲
你会发现直线也可以走? 离谱!
最终的解决方案是

return isAdj(GridPoint, targetGridPoint)&&  isAdj(GridPoint, targetGridPoint) && HasGridMeetCondition(Map, targetGridPoint, Ground, Box);

//判断一个方格是否可达(未在关闭列表且相邻)
bool IsReachGrid(const AIGrid* Grid, const AIGrid* targetGrid) {

	AIPathMap& Map = AStarAutoPaths->Map;   // 地图

	auto& PathMap = Map.map;                 // 地图数据
	const AIpoint& GridPoint = Grid->point;   // 当前方格坐标
	const AIpoint& targetGridPoint = targetGrid->point; // 目标方格坐标

	if ((IsCoordInMap(Map, targetGridPoint) ||   // 目标方格在地图内或
		(DoesGridMeetCondition(Map, targetGridPoint, Ground, Box) &&   // 满足条件且与当前方格相同 
			AreCoordsEqual(GridPoint, targetGridPoint)) ||
		isInList(AStarAutoPaths->CloseList, targetGrid))) {   // 目标方格在关闭列表中
		return false;
	}
					// 相邻方格				     // /满足条件
	return isAdj(GridPoint, targetGridPoint) && DoesGridMeetCondition(Map, targetGridPoint, Ground, Box); 
}

         0 0 0 0 0 0 0 0 0 0 0 0 0 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 2 1 1 0 1 3 1 1 1 0
         0 1 1 1 1 1 1 0 1 1 1 1 1 0
         0 1 1 1 1 1 1 1 1 1 1 1 1 0
         0 0 0 0 0 0 0 0 0 0 0 0 0 0

        坤坤:   方格坐标  x =4   方格坐标 y =4  到      宝箱:   方格坐标  x =4   方格坐标 y =9
        方格坐标  x =4   方格坐标 y =4  方格策略 G =0   方格策略H =0    方格策略F =0
        方格坐标  x =4   方格坐标 y =5  方格策略 G =10  方格策略H =12   方格策略F =22
        方格坐标  x =4   方格坐标 y =6  方格策略 G =10  方格策略H =9    方格策略F =19
        方格坐标  x =5   方格坐标 y =6  方格策略 G =20  方格策略H =9    方格策略F =29
        方格坐标  x =6   方格坐标 y =6  方格策略 G =20  方格策略H =9    方格策略F =29
        方格坐标  x =6   方格坐标 y =7  方格策略 G =30  方格策略H =6    方格策略F =36
        方格坐标  x =6   方格坐标 y =8  方格策略 G =30  方格策略H =3    方格策略F =33
        方格坐标  x =5   方格坐标 y =8  方格策略 G =40  方格策略H =2    方格策略F =42
        方格坐标  x =4   方格坐标 y =8  方格策略 G =40  方格策略H =1    方格策略F =41
        方格坐标  x =4   方格坐标 y =9  方格策略 G =50  方格策略H =0    方格策略F =50