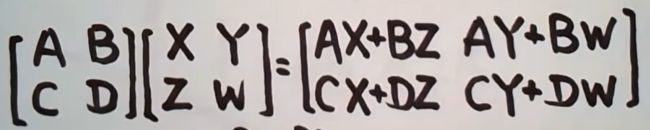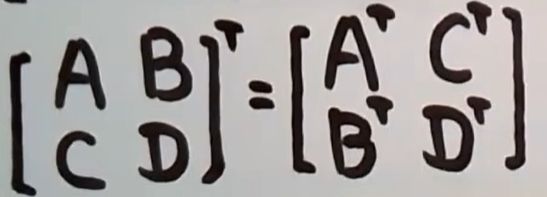【考研线代】二. 矩阵
文章目录
- 第二章 矩阵
-
- 2.1 概念,运算
-
- 2.1.1 概念
- 2.1.2 运算
- 2.1.3 运算法则
- 2.2 伴随矩阵,可逆矩阵(非奇异矩阵)
-
- 2.2.1 伴随矩阵
- 2.2.2 可逆矩阵
- 2.3 初等变换,初等矩阵
-
- 2.3.1 概念
- 2.3.2 重要结论
- 2.4 分块矩阵
-
- 2.4.1 运算法则
- 2.4.2 解题技巧
- 2.5 方阵的行列式
- 2.6 相关错题
- 2.7 补充
-
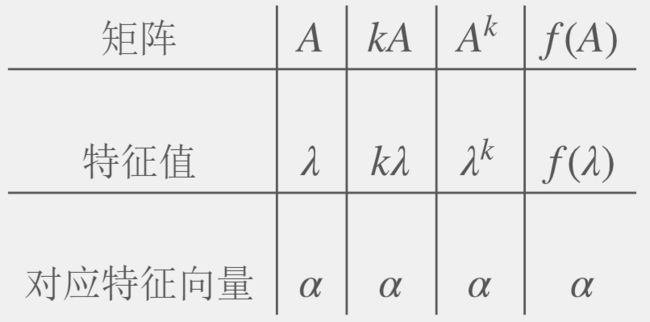
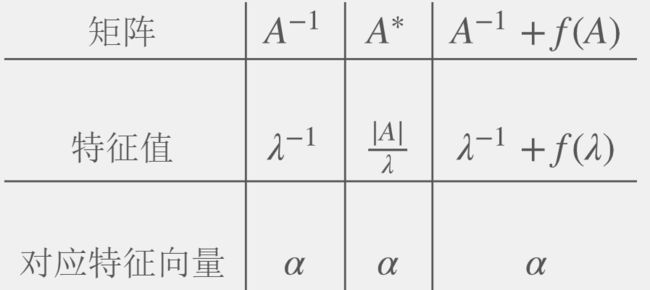
- 2.7.1 特征值和不同矩阵的对应关系
- 2.7.2 通法:求解矩阵的逆(二三阶)
第二章 矩阵
2.1 概念,运算
2.1.1 概念
矩阵,n阶矩阵,n阶方阵,零矩阵,同型矩阵(行数与列数分别相等),矩阵相等。
2.1.2 运算
- 加法:对应位置相加。要求矩阵同型。
- 数乘:全部位置乘数。
- 乘法:对应相加的A行乘B列 。要求A列数= B行数。
- 幂次:A的k次幂(乘k次自己)。要求A是n阶方阵。
2.1.3 运算法则
- 加法:满足交换律和结合律
- 乘法:满足结合律,分配律。但是不满足交换律。
- 数乘矩阵:满足结合律和分配律。
- 转置(行列互换):这个需要特别注意下。
( A + B ) T = A T + B T (A+B)^T = A^T + B^T (A+B)T=AT+BT
( k A ) T = k A T (kA)^T = k A^T (kA)T=kAT
( A B ) T = B T A T (AB)^T = B^TA^T (AB)T=BTAT
( A T ) T = A (A^T)^T = A (AT)T=A
特例
- 对角线矩阵相乘,直接乘对角线上面的元素。
- n维列向量 × n维行向量 = n阶矩阵
- n维行向量 × n维列向量 = 1*1矩阵
疑问点
- 线性代数n维行向量乘n维列向量结果为什么说是一个数 ? 为什么不是一个一行一列的矩阵?
2.2 伴随矩阵,可逆矩阵(非奇异矩阵)
2.2.1 伴随矩阵
伴随矩阵:矩阵A对应行列式|A|的所有代数余子式构成的矩阵A*
注意:伴随矩阵第一行第二个的值 是 去除了第二行第一个的值的代数余子式。
相关公式:
A A ∗ = A ∗ A = ∣ A ∣ E AA^* = A^* A = |A|E AA∗=A∗A=∣A∣E
( A ∗ ) − 1 = ( A − 1 ) ∗ = A ∣ A ∣ (A^*)^{-1} = (A^{-1})^* = \frac{A}{|A|} (A∗)−1=(A−1)∗=∣A∣A
( k A ) ∗ = k n − 1 A ∗ (kA)^* = k^{n-1}A^* (kA)∗=kn−1A∗
( A ∗ ) T = ( A T ) ∗ (A^*)^T = (A^T)^* (A∗)T=(AT)∗
∣ A ∗ ∣ = ∣ A ∣ n − 1 |A^*| = |A|^{n-1} ∣A∗∣=∣A∣n−1
( A ∗ ) ∗ = ∣ A ∣ n − 2 A ( n > = 2 ) (A^*)^* = |A|^{n-2}A (n>=2) (A∗)∗=∣A∣n−2A(n>=2)
秩:
r ( A ∗ ) = { n , r ( A ) = n 1 , r ( A ) = n − 1 0 , r ( A ) < n − 1 r(A^*) = \left\{\begin{matrix}n,r(A)=n \\ 1,r(A)=n-1 \\0,r(A)
技巧
二阶矩阵的求法口诀:主对角线元素互换,副对角线元素加负号。
2.2.2 可逆矩阵
若AB = BA = E,则称A是可逆矩阵或非奇异矩阵。
定理:
- 若A可逆,则 A的逆矩阵唯一(证明:加单位矩阵,再变形)
- A可逆 <=> |A|!=0
- AB均为n阶且AB = E,则BA = E (可逆)
求逆方法:
-
定义法:AB=E
-
用伴随关系:(适用2,3阶)
A − 1 = 1 ∣ A ∣ A ∗ A^{-1} = \frac{1}{|A|} A^* A−1=∣A∣1A∗ -
初等行变换(A|E):右侧加一个等阶的单位矩阵,化简左侧的矩阵到单位矩阵,右侧的矩阵就是逆矩阵了。
-
分块对角线矩阵:左下角和右上角若为0矩阵,则可以令对角线上的矩阵分别求逆。
2.3 初等变换,初等矩阵
2.3.1 概念
-
初等变换:初等行变换 + 初等列变换
- 初等行变换:倍乘,互换,倍加
- 初等列变换:等价,同上。
-
初等矩阵:单位矩阵 经过 一次 初等变换 所得到的矩阵
- 倍乘初等矩阵:E(i(k))
- 互换初等矩阵: E(i,j)
- 倍加初等矩阵:E(ij(k))
-
行阶梯矩阵:A-m×n,满足:(看起来像阶梯)
- 零行在最底下
- 非零行的主元的列指标随行指标递增而严格增大。
-
行最简矩阵:
- 满足行阶梯
- 主元都是1 且 主元所在的列其他元素都是0.
-
矩阵等价,A经过有限次初等变换得到矩阵B,A等价于B.
- 充要条件:秩相等(r(A) = r(B))
2.3.2 重要结论
-
初等矩阵的转置仍是初等矩阵。
-
初等矩阵 均是可逆矩阵,逆矩阵也是初等矩阵。
-
互换行的逆矩阵是它自己
E ( i , j ) − 1 = E ( i , j ) E(i,j)^{-1} = E(i,j) E(i,j)−1=E(i,j) -
倍乘的逆矩阵是它的倒数
E ( i ( k ) ) − 1 = E ( i ( 1 k ) ) E(i(k))^-1 = E(i(\frac{1}{k})) E(i(k))−1=E(i(k1)) -
倍乘的逆矩阵改成倍乘相反数
E ( i j ( k ) ) − 1 = E ( i j ( − k ) ) E(ij(k))^{-1} = E(ij(-k)) E(ij(k))−1=E(ij(−k))
-
-
初等矩阵P左乘矩阵A,其乘积PA,就是矩阵A作一次与P相同的行变换。
-
初等矩阵P右乘矩阵A,其乘积AP,就是矩阵A做一次与P相同的列变换。
2.4 分块矩阵
2.4.1 运算法则
2.4.2 解题技巧
解题技巧1
遇到矩阵乘法,矩阵的幂,矩阵的逆都可以考虑。
解题技巧2
遇到方程组求解,可以考虑按列分块,遇到向量组的秩或按行分块后,转换成向量,秩的关系求解。
-
若AB = C,则C的行向量可以由B的行向量线性表出。
-
若给出AX = B,求X:
- 若A可逆,可以通过左乘一个A的逆。
- 若A不可逆,可以通过构造X的列向量,重新求小块变量。
2.5 方阵的行列式
主要用于抽象n阶方阵行列式的计算
1. 转 置 矩 阵 的 行 列 式 不 变 : ∣ A T ∣ = ∣ A ∣ 1.转置矩阵的行列式不变: |A^T| = |A| 1.转置矩阵的行列式不变:∣AT∣=∣A∣
2. 数 乘 矩 阵 的 行 列 式 , 是 原 行 列 式 的 n 次 方 倍 : ∣ k A ∣ = k n ∣ A ∣ 2. 数乘矩阵的行列式,是原行列式的n次方倍:|kA| = k^n|A| 2.数乘矩阵的行列式,是原行列式的n次方倍:∣kA∣=kn∣A∣
3. 两 矩 阵 相 乘 的 行 列 式 : ∣ A B ∣ = ∣ A ∣ ∣ ∣ B ∣ 3. 两矩阵相乘的行列式:|AB| = |A|||B| 3.两矩阵相乘的行列式:∣AB∣=∣A∣∣∣B∣
3. 推 论 : ∣ A 2 ∣ = ∣ A ∣ 2 3.推论:|A^2| = |A|^2 3.推论:∣A2∣=∣A∣2
4. 逆 矩 阵 的 行 列 式 关 系 : ∣ A − 1 ∣ = ∣ A ∣ − 1 4. 逆矩阵的行列式关系: |A^{-1}| = |A|^{-1} 4.逆矩阵的行列式关系:∣A−1∣=∣A∣−1
5. 伴 随 矩 阵 的 行 列 式 关 系 : ∣ A ∗ ∣ = ∣ ∣ A ∣ A − 1 ∣ = ∣ A ∣ n − 1 5. 伴随矩阵的行列式关系: |A^*| = |{|A|}A^{-1}|= |A|^{n-1} 5.伴随矩阵的行列式关系:∣A∗∣=∣∣A∣A−1∣=∣A∣n−1
2.6 相关错题
好像都和秩有关,不知道后面会不会理解一点。
已 知 A = [ 2 − 1 3 4 − 2 6 − 2 1 − 3 ] , 求 A 10 已知A = \left[ \begin{matrix} 2 & -1 & 3 \\ 4 & -2 & 6 \\ -2 & 1 & -3 \\ \end{matrix} \right] ,求A^{10} 已知A=⎣⎡24−2−1−2136−3⎦⎤,求A10
看到第一行和第三行等比例误以为是行列式直接等0了
解析:
r ( A ) = 1 = > A 2 = l A , 其 中 l = ∑ a i i r(A)=1 => A^2=lA,其中l=\sum a_{ii} r(A)=1=>A2=lA,其中l=∑aii
所 以 , A n = l n − 1 A 所以,A^n = l^{n-1}A 所以,An=ln−1A
A 10 = ( 2 + ( − 2 ) + ( − 3 ) ) 9 A A^{10} = (2+(-2) + (-3))^{9}A A10=(2+(−2)+(−3))9A