关于动态规划解决最长公共子序列
关于动态规划解决最长公共子序列
最长公共子序列问题是动态规划的经典问题之一,描述如下:
给定两个序列X和Y,当另一序列Z既是X的子序列又是Y的子序列,则称Z是X和Y的公共子序列,求最长的公共子序列Z。
动态规划第一步:构造具有最优子结构的解结构
设X={x1,x2,x3,…,xm},Y={y1,y2,y3,…,yn}的最长公共子序列为Z={z1,z2,z3,…,zk}。
那么由问题的描述可知X,Y,Z有如下性质:
①若xm=yn,则zk=xm=yn,那么Zk-1是Xm-1和Yn-1的最长公共子序列。
(①的思路:很显然,当X和Y的最后一个值相等时,无论前面的公共子序列是什么,公共子序列的最后一个值就是xm的值)
②若xm≠yn,且zk≠xm,则Z是Xm-1和Y的最长公共子序列。
③若xm≠yn,且zk≠yn,则Z是X和Yn-1的最长公共子序列。
(②和③的思路:显然由①反推可知,如果X与Y最后一个子元素不同,那么X和Y的最后一位至少有一个不是公共子序列的最后一位,如果X的最后一位不是公共子序列的最后一位,那么对于本题需要求的公共子序列来说X与Xm-1没有任何区别,可以将X最后一位删去,如果Y的最后一位不是公共子序列的最后一位,那么删去Y的最后一位也不会影响公共子序列。)
至此,第一步完成。
动态规划第二步:根据最优子结构的性质得出递推式
递归式已经隐含于①所构造出来的最优子结构了。
用c[i][j]记录序列Xi和Yj的最长公共子序列的长度,其中
Xi={x1,x2,x3,…,xi};Yj={y1,y2,y3,…,yj}
那么由前述的三种情况可以推知:
①当i=0 或 j=0时,c[i][j]=0;
解释:如果有一个序列是空序列,自然最长公共子序列长度为0。
②当i,j>0;xi=yj时,c[i][j]=c[i-1][j-1]+1
解释:这一条是由①性质得出的,因为Zk-1是Xm-1与Yn-1的最长公共子序列,那么Zk的长度自然是Xm-1与Yn-1的最长公共子序列长度+1。
③当i,j>0;xi≠yj时,c[i][j]=max{c[i][j-1],c[i-1][j]}
解释:这一条是由②和③性质共同得出的,因为如果X与Y最后一个子元素不同,那么X和Y的最后一位至少有一个不是公共子序列的最后一位。也就是X序列与Y序列至少有一个能删去最后一位。但由于计算c[i][j]时,我们无法得知公共序列Z的最后一位zk是什么,无法拿去与xi,yj比较,所以无法得知应该删去X序列的最后一位(c[i][j]=c[i-1][j])还是删去Y序列的最后一位(c[i][j]=c[i][j-1]),只能将两种情况都计算出来,再比较他们的大小,留下序列最长的放入c[i][j]。
至此,第二步完成。
动态规划第三步:根据递归关系,设计算法计算最优值。
计算最优值的算法实际上就是计算c[i][j],写代码前先整理下c[i][j]的计算原理:
由第二步得出的c[i][j]的分段函数可知:若将c[i][j]看做二维矩阵,c[i][j]的计算总是依赖与其左(c[i][j-1])、上(c[i-1][j])、左上(c[i-1][j-1])这三个坐标的值,所以计算的顺序应当是自左向右,自上而下。
在网上找到的一幅图:
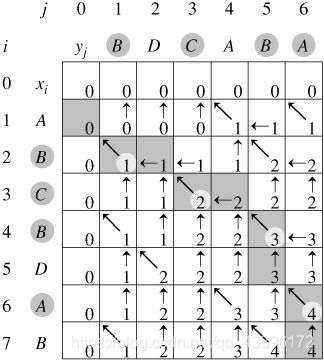
这幅图的意思是:xi序列为{A,B,C,B,D,A,B},yj序列为{B,D,C,A,B,A}。
由于左边边界和上方边界没有左(c[i][j-1])、上(c[i-1][j])、左上(c[i-1][j-1])这三个坐标,所以额外设置了一个第0行与第0列,全部都置为了0,方便算法计算。
先以c[4][3]的计算为例,比较x4和y3,由于x4=B,y3=C,x4≠y3,所以属于第三个递推式c[i][j]=max{c[i][j-1],c[i-1][j]},求其左方坐标的值c[i][j-1]和上方坐标的值c[i-1][j],比较取最大者,由于c[4][2]=1,c[3][3]=2,所以c[4][3]=c[3][3]=2。
再以c[4][5]的计算为例,比较x4和y5,由于x4=B,y5=B,x4=y5,所以属于第二个递推式c[i][j]=c[i-1][j-1]+1。即其左上角坐标的值+1,c[4][5]=c[3][4]+1=2+1=3。
代码如下:
//m是X序列的长度,n是Y序列的长度,ps而实际上因为多增加了一行一列,表示它们的数组的长度增加了1
//x是X序列(数组)的首地址,y是Y序列(数组)的首地址
//c是上文提到的记录最长公共子序列长度的二维数组c[][]
//b是用于第四步构造最优解的一个二维矩阵,第四步时再说。
void LCSLength(int m,int n,char *x,char *y,int **c,int **b){
int i,j;
//下面的两个循环就是把额外加的第0行与第0列置0,防止左边界和上边界越界
for(i=0;i<=m;i++)
c[i][0] = 0;
for(i=1;i<=n;i++)
c[0][j] = 0;
//下面的双重循环就是自左向右,自上而下的开始计算c[][]
for(i=1;i<=m;i++){
for(j=1;j<=m;j++){
if(x[i]==y[j]){
c[i][j]=c[i-1][j-1]+1;
b[i][j]=1;
}
//若x[i]≠y[j],则计算左边和上面坐标的值,取最大者
else if(c[i-1][j]>=c[i][j-1]){
c[i][j]=c[i-1][j];
b[i][j]=2;
}
else {
c[i][j]=c[i][j-1];
b[i][j]=3;
}
}
}
}
相信理解了上面的解说之后,代码肯定很简单了。
动态规划第四步:构造最优解,根据算法获取的信息构造出最长公共子序列。
根据算法得到表示最长公共子序列的二维矩阵c[m][n]之后,我们已经知道,Xm与Yn的最长公共子序列的长度就是c[m][n],也就是矩阵中最右下角、最后一个数值。但c[m][n]只是最长公共子序列的长度而已,而我们需要的是最长公共子序列Zk,很明显的一点就是,必须要从c[m][n]开始回溯我们才知道最优子序列是什么,但很明显,回溯是有歧义的,有时向数个方向回溯都能满足要求,必须消除这种歧义。
而这就是代码中b[m][n]矩阵的意义,由于c[i][j]的计算只能从三个方向左(c[i][j-1])、上(c[i-1][j])、左上(c[i-1][j-1]),那么只需要设置一个b[i][j]记录下c[i][j]是从哪个方向上获取值的,我们就能没有歧义的从c[m][n]回溯回起点,从而找出Zk序列。可以规定:b[i][j]=1,意味着c[i][j]的值是从左上c[i-1][j-1]+1而来,b[i][j]=2,意味着c[i][j]的值是从上面c[i-1][j]而来,b[i][j]=3,意味着c[i][j]的值是从左边c[i][j-1]而来。

敏锐一点应该就能发现了,b[m][n]的作用其实就是图中的箭头,箭头所指就是回溯的路径,回溯路径中任一一个b[i][j],只要满足x[i]=y[j](字符相等),就意味着它是最长公共子序列中的一个,回溯会直到左边界和上边界为止。(因为左边界和上边界是c[i][j]=0,这意味着最长公共子序列长度为0。)
原理清楚后,上代码:
void LCS(int i,int j,char *x,int **b){
//下面是递归的出口,当i或j=0时,c[i][j]==0,所以没有公共子序列了。
if(i==0||j==0)
return;
//b[i][j]==1时,x[i]==y[j],这是赋值b的时候就确定的事情,所以满足前面总结的规律。
if(b[i][j]==1){
LCS(i-1,j-1,x,b);
cout<<x[i];
}
//如果b[i][j]==2,那么说明x[i]≠y[j],自然也就不属于公共子序列,然后再继续回溯,下面一个也是同理。
else if(b[i][j]==2)
LCS(i-1,j,x,b);
else
LCS(i,j-1,x,b);
}