leetcode64. 最小路径和(动态规划-java)

leetcode64. 最小路径和

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/minimum-path-sum

题目描述

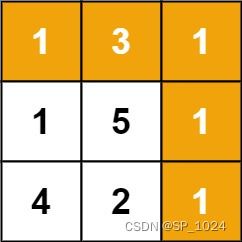
给定一个包含非负整数的 m x n 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。
说明：每次只能向下或者向右移动一步。

示例1:

输入：grid = [[1,3,1],[1,5,1],[4,2,1]]
输出：7
解释：因为路径 1→3→1→1→1 的总和最小。

示例 2：
输入：grid = [[1,2,3],[4,5,6]]
输出：12

提示：
m == grid.length
n == grid[i].length
1 <= m, n <= 200
0 <= grid[i][j] <= 200

暴力递归 + 缓存

最小路径和的问题,是一类问题.我们是有两个方向,向下和向右,我们递归时,要去判断这两种结果下来,哪个路径和最小.
在图中要做好边界值判断.

代码演示

	/**
	* 最小路径和
	*/
    public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        int[][]dp = new int[n][m];
        return process1(grid,0,0,dp);
    }

/**
* 暴力递归
* dp 缓存
* 
*/
 public int process1(int[][] grid,int i,int j,int[][]dp){
 		// 到右下角最后一个位置时, 结束,返回最右下角的值
          if(i == grid.length - 1  && j == grid[0].length - 1 ){
              return grid[i][j];
          }
          //一个方向上越界时, 返回一个无效值
          if( i >= grid.length || j >=  grid[0].length  ){
              return Integer.MAX_VALUE;
          }
          //缓存中如果有值的话,从缓存中拿
          if(dp[i][j] != 0){
              return dp[i][j];
          }
          //两个方向上比较的最小值,加上当前位置上的值,是最小值
          int res = Math.min(process1(grid,i + 1,j,dp) ,
                process1(grid,i,j + 1,dp)) + grid[i][j];
          //结果放进缓存中
          dp[i][j] = res ;
          return res;
    }

动态规划

动态规划就是对暴力递归的改写.三个步骤
1.初始化dp 表的值.
第一行的值,因为没有从上面方向的值,所以只能是从左往右相加
第一列的值,因为没有从右面方向的值,所以只能从上往下相加
2. 根据递归过程找出状态转移方程
dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
3.返回最右下角的值,

代码演示

 public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        int[][]dp = new int[n + 1][m + 1];
         dp[0][0] = grid[0][0];
         //第一行的值,只能从左往右相加,没有上方的值
        for (int i = 1; i < m;i++){
            dp[0][i] = dp[0][i - 1] + grid[0][i] ;
        }
          //第一列的值,只能从上往下相加,没有左边的值
        for (int j = 1; j < n;j++){
           dp[j][0] = dp[j - 1][0] + grid[j][0];
        }

        for (int i = 1; i < n ;i++){
            for (int j = 1; j < m ;j++){
            //状态转移方程.
                dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
            }
        }
        return dp[n - 1][m - 1];
    }

空间压缩

状态转移方程是: dp[i][j] = Math.min(dp[i - 1][j],dp[i][j - 1]) + grid[i][j];
但是我们最后只要了 return dp[n - 1][m - 1] 最后一行的右下角的值,
所以我们可以用一行的的数据,不断滚动的向下更新,
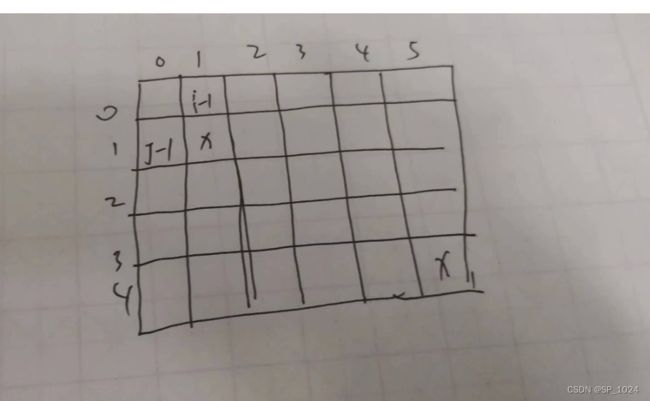
用图演示

x位置的值依赖i- 1 和 j - 1 的值,我们就不需要二维数组了,我们用一个单数组,不断向下滚动更新,每次更新时,我们提前把j - 1 位置的数更新出来,然后从左向右更新值,

代码演示

     public int minPathSum(int[][] grid) {
        int n = grid.length;
        int m = grid[0].length;
        int[]dp = new int[m + 1];
        dp[0] = grid[0][0];
        for (int i = 1; i < m;i++){
            dp[i] = dp[i - 1] + grid[0][i] ;
        }

        for (int i = 1; i < n ;i++){
        //每次先把最左边的值更新出来下面在从左往右更新值
            dp[0] = dp[0] + grid[i][0];
            for (int j = 1; j < m ;j++){
                
                dp[j] = Math.min(dp[j - 1] ,dp[j]) + grid[i][j];
            }
        }
        return dp[m - 1];
    }

动态规划专题

leetcode416. 分割等和子集

leetcode354. 俄罗斯套娃信封问题

leetcode300. 最长递增子序列

leetcode213. 打家劫舍 II

leetcode198. 打家劫舍

leetcode337. 打家劫舍 III