熵、KL散度和交叉熵

首先我们需要知道，所有的模型都可以看作是一个概率分布模型，包括人脑进行图像分类时也可以看作是一种完美的模型

1、信息量

如果学过通信应该知道香农定义了信息量的的概念，我们能够理解一件事情信息量很大或者很小，但是如何用数学去描述信息量具体是多大？

很明显一件事情发生的概率越大其信息量越小。概率越小其信息量越大。比如太阳明天从东边升起，这是没有什么信息量的。但是太阳明天从西边升起，信息量就非常大。在生活中我们遇到一些三观炸裂的事情，也会说这信息量好大，让我捋一捋。

所以事件$x$的信息量定义为：$$f(x)=-lo{g}_{2}p(x)$$其中$p(x)$为事件$x$的概率。因为概率越大信息量越小，所以前面的负号使得$f(x)$满足单调递减。这里的$log$只是一种定义形式，如果愿意也可以用其他数学表达式，只不过$log$有自在的好处而已。底数为2使得信息量的单位为比特。

2、熵

熵是用于衡量系统混乱程度的指标。高中我们学过熵总是自然趋向熵增的，也就是世界是自发熵增的，会越来越混乱。

熵的定义其实就是该系统中各事件信息量的加权和。为什么要加权和？如果一个事件概率很低，则其信息量很高，整个系统的熵就由其主导了。但是该事件发生的概率是很低的，所以由其概率作为加权和的权重加权后就可以得到平衡。

熵的数学定义为：$$H=p(x_1)f(x_1)+p(x_2)f(x_2)+......=\sum p(x_i)f(x_i)$$其中$f(x_i)$为事件$x_i$的信息量，$p(x_i)$为其概率。其实$p(x_i)$就是加权和的权重。

将信息量的公式带入熵H中，可以得到：$$H=\sum p(x_i)f(x_i)=\sum p(x_i)[-lo{g}_{2}p(x_i)]=-\sum p(x_i)lo{g}_{2}p(x_i)$$

3、KL散度（相对熵、互熵）

现在我们知道了熵，如何利用熵衡量两个模型的相似度？KL散度就可以衡量。

比如上面有两个模型，有m个事件（或者有m个类）。假设现在P为基准模型（标签），Q模型为拟合模型（训练的模型），现在来衡量Q和基准P之间的差距：$$D_{KL}(P||Q)=\sum p_i(f_Q(q_i)-f_P(p_i))$$
其中$f$为信息量。从公式可以看到，两个分布的"差距"就是信息量差值的加权和，也就是相对熵（信息量的加权和是系统的熵，信息量差值的加权和就是两个系统的相对熵）。

将信息量定义代入可得：
$$\begin{array}{rl}{D}_{KL}(P||Q)& =\sum p_i(-lo{g}_2{q}_i--lo{g}_2{p}_i)\\ & =\sum p_i(-lo{g}_2{q}_i)-\sum p_i(-lo{g}_2{p}_i)\\ & =part1-part2\end{array}$$
首先part1就是交叉熵（从公式可以看出是P的概率\*Q的信息量，就是交叉之义，概率\*信息量就是熵之义，所以part1就是交叉熵）

其次part2是基准模型P的熵，而基准模型在拟合过程中是充当标准的作用，是不会变的，所以part2就是一个常量。

所以在训练的时候只需要$D_{KL}$越小越好，但是我们并不知道基准的熵part2是多少，但是不用担心我们只要保证part1越小，Q的分布就越拟合基准分布P。

可能有人疑惑我们并不知道part1和part2谁大谁小，所以要求$D_{KL}$越小时不能保证part1越小。但是吉布斯不等式已经帮我们证明了$D_{KL}$≥恒成立（也就是part1≥part2恒成立）。所以在实际使用时我们只需要保证part1越小越好（也就是交叉熵越小越好）。

4、交叉熵公式和网络模型的参数如何对应？

我们已经知道part2就是交叉熵：$$CE=\sum p_i(-lo{g}_2{q}_i)$$
我们定义一个二分类模型，样本标签为$x$的样本的概率为$x$，模型为$f$，则有$y=f_{W,b}(x)$，$y$为预测出的类别概率。标签$x$为独热编码，$y$为模型的输出，即该样本在各个类上的概率分布。

举个例子，现在有二分类任务识别图片是否为猫，假设某个图片标签为猫，则有：

类别	标签 P	预测 Q
猫	1	0.8
非猫	0	0.2

基准分布和预测分布（可以和上面的图对照看，上面的图有多个类别，这里只有两个类别）：

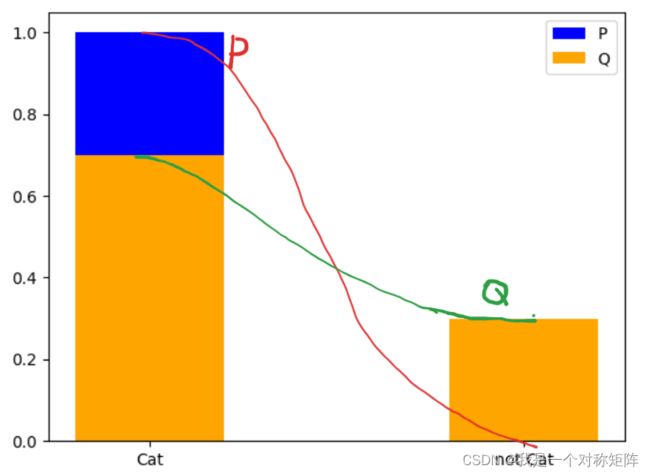
对于是猫的某个样本img1，其标签为类0，则独热编码(基准P的分布)=[1,0]。其预测分布(Q)为[0.7,0.3]，则
$$-C{E}_{img1}=x_{cat}lo{g}_2{y}_{cat}+x_{notcat}lo{g}_2(y_{notcat})$$
因为$x_{cat}+x_{notcat}=1$且$y_{cat}+y_{notcat}=1$，故可以写为$$-C{E}_{img1}=x_{cat}lo{g}_2{y}_{cat}+(1-x_{cat})lo{g}_2(1-y_{cat})=xlo{g}_{2}y+(1-x)lo{g}_2(1-y)$$
其实就是类别’猫’类别的交叉熵和’非猫’类别的交叉熵的和，即所有类别的交叉熵的和。

以上是两个类别的交叉熵，推广之，对于多分类n的交叉熵公式就是所有类别交叉熵的和：
$$CE=-\sum x_{i}lo{g}_2{y}_i$$

给定一张图模型输出的值一定在任何类上都有一定的概率值即$y_i$是一个向量，实际上因为独热编码的原因，$x_i$非标签位上的为0，仅在标签为上为1，所以公式等效为$$CE=-\sum lo{g}_2{y}_i$$比如有2个样本，其标签为[0,2]，则其独热编码为[[1,0,0],[0,0,1]]，其预测概率为[[09,0.1,0],[0.1,0.1,.08]]，所以交叉熵为$-(lo{g}_{2}0.9+lo{g}_{2}0.8)\approx 0.47$

然而当我们使用pytorch的交叉熵函数计算时，发现等于0.65：

import torch

target = torch.tensor([0, 2], dtype=torch.int64)
prob = torch.tensor([[0.9, 0.1, 0], [0.1, 0.1, 0.8]], dtype=torch.float32)

loss = torch.nn.CrossEntropyLoss()(prob, target)
print(loss) # 0.65

5、Pytorch中的交叉熵

Pytorch中CrossEntropyLoss()函数的主要是将softmax-log-NLLLoss合并到一块得到的结果。

• Softmax后的数值都在0~1之间，log计算就是负值了。（也就是分类网络最后一层为softmax，pytorch中一般整合到交叉熵损失函数中了）

• 然后将Softmax之后的结果取$lo{g}_e$ ，底数其实没有什么规定，都只是数学定义，不管公式中底数为2还是e，只要符合需求就都是正确的理论。

• NLLLoss就是和独热编码相乘求和的过程（注意添加符号），

具体过程如下图

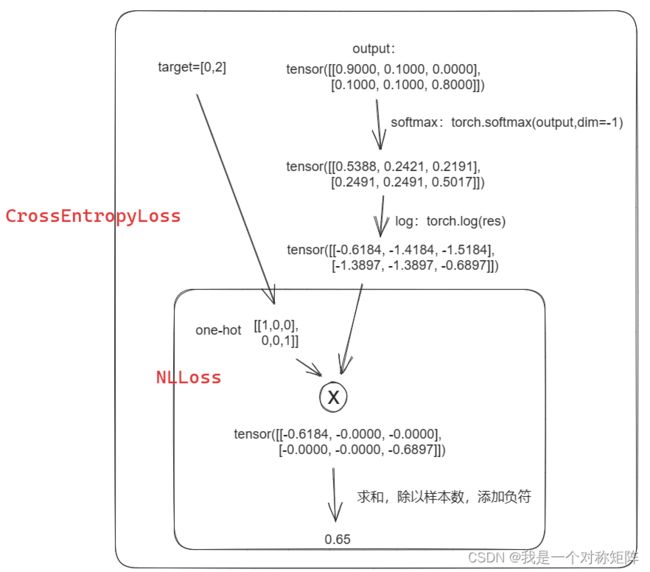
至此基本就结束了，其实交叉熵就是标签和log概率的乘积，即标签位置的信息量是多少（我们希望在该位置上的概率和标签一样同样是1，概率为1即信息量为0，此时交叉熵为0，这就是网络训练的目标），然后在样本尺度求均值就是批次的交叉熵。