随机森林算法

1. 随机森林原理

1.1 集成学习

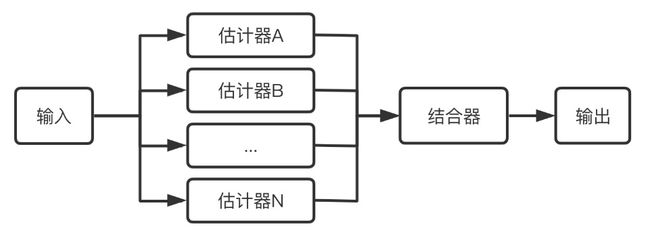
集成学习通过训练学习出多个估计器，当需要预测时通过结合器将多个估计器的结果整合起来当作最后的结果输出。

下图展示了集成学习的基本流程：

集成学习分两种：
（1）Bagging装袋：又称自主聚集(bootstrap aggregating)，是一种根据均匀概率分布从数据集中重复抽样（有放回）的技术。每个新数据集和原始数据集大小相等。代表算法：随机森林。
（2）Boosting提升：是一个迭代的过程，用来自适应地改变训练样本的分布，使得弱学习器聚焦到那些很难分类的样本上。它的做法是给每一个训练样本赋予一个权重，在每一轮训练结束时自动地调整权重。代表算法：Adaboost、GBDT、XGBoost。

集成学习的优势是提升了单个估计器的通用性与鲁棒性，比单个估计器拥有更好的预测性能。集成学习的另一个特点是能方便的进行并行化操作。

1.2 Bagging算法

Bagging 算法是一种集成学习算法，其全称为自助聚集算法（Bootstrap aggregating），顾名思义算法由 Bootstrap 与 Aggregating 两部分组成。

下图展示了Bagging算法使用自助取样（Bootstrapping）生成多个子数据的示例：

算法的具体步骤为：假设有一个大小为 N 的训练数据集，每次从该数据集中有放回的取选出大小为 M 的子数据集，一共选 K 次，根据这 K 个子数据集，训练学习出 K 个模型。当要预测的时候，使用这 K 个模型进行预测，再通过取平均值或者多数分类的方式，得到最后的预测结果。

1.3 随机森林算法

将多个决策树结合在一起，每次数据集是随机有放回的选出，同时随机选出部分特征作为输入，所以该算法被称为随机森林算法。可以看到随机森林算法是以决策树为估计器的Bagging算法。

上图展示了随机森林算法的具体流程，其中结合器在分类问题中，选择多数分类结果作为最后的结果，在回归问题中，对多个回归结果取平均值作为最后的结果。

使用Bagging算法能降低过拟合的情况，从而带来了更好的性能。单个决策树对训练集的噪声非常敏感，但通过Bagging算法降低了训练出的多颗决策树之间关联性，有效缓解了上述问题。

2. 随机森林算法步骤

假设训练集 T 的大小为 N ，特征数目为 M ，随机森林的树的数量为 K ，随机森林算法的具体步骤如下：
重复下面步骤 K 次，即生成K棵决策树，形成随机森林：
第一步：从训练集 T 中有放回抽样的方式，取样N 次形成一个新子训练集 D；
第二步：随机选择 m 个特征，其中 m < M；
第三步：使用新的训练集 D 和 m 个特征，学习出一个完整的决策树（一般是CART）。

3. 随机森林特点

优点：
（1）实现简单，泛化能力强，可以并行实现，因为训练时树与树之间是相互独立的；
（2）相比单一决策树，能学习到特征之间的相互影响，且不容易过拟合；
（3）能直接特征很多的高维数据，因为在训练过程中依旧会从这些特征中随机选取部分特征用来训练；
（4）相比SVM，不是很怕特征缺失，因为待选特征也是随机选取；
（5）训练完成后可以给出特征重要性。当然，这个优点主要来源于决策树。因为决策树在训练过程中会计算熵或者是基尼系数，越往树的根部，特征越重要。

缺点：
（1）在噪声过大的分类和处理回归问题时还是容易过拟合；
（2）相比于单一决策树，它的随机性让我们难以对模型进行解释。

4. 随机森林的Python应用

Sklearn的ensemble库中提供了随机森林分类和回归的方法，分别是ensemble.RandomForestClassifier([…])随机森林分类和ensemble.RandomForestRegressor([…])随机森林回归。

4.1 RandomForestClassifier随机森林分类

RandomForestClassifier函数原型如下：

RandomForestClassifier(n_estimators=100, *, criterion='gini', max_depth=None,min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features='auto', max_leaf_nodes=None, min_impurity_decrease=0.0,min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=None, random_state=None, verbose=0, warm_start=False, class_weight=None,ccp_alpha=0.0, max_samples=None)

参数说明：

n_estimators：森林中决策树的数量。默认100。

criterion：分裂节点所用的标准，可选“gini”, “entropy”，默认“gini”。

max_depth：树的最大深度。如果为None，则将节点展开，直到所有叶子都是纯净的(只有一个类)，或者直到所有叶子都包含少于min_samples_split个样本。默认是None。

min_samples_split：拆分内部节点所需的最少样本数：如果为int，则将min_samples_split视为最小值。如果为float，则min_samples_split是一个分数，而ceil（min_samples_split * n_samples）是每个拆分的最小样本数。默认是2。

min_samples_leaf：在叶节点处需要的最小样本数。仅在任何深度的分割点在左分支和右分支中的每个分支上至少留下min_samples_leaf个训练样本时，才考虑。这可能具有平滑模型的效果，尤其是在回归中。如果为int，则将min_samples_leaf视为最小值。如果为float，则min_samples_leaf是分数，而ceil（min_samples_leaf * n_samples）是每个节点的最小样本数。默认是1。

min_weight_fraction_leaf：在所有叶节点处（所有输入样本）的权重总和中的最小加权分数。如果未提供sample_weight，则样本的权重相等。

max_features：寻找最佳分割时要考虑的特征数量：如果为int，则在每个拆分中考虑max_features个特征。如果为float，则max_features是一个分数，并在每次拆分时考虑int（max_features * n_features）个特征。如果为“auto”，则max_features = sqrt（n_features）。如果为“ sqrt”，则max_features = sqrt（n_features）。如果为“ log2”，则max_features = log2（n_features）。如果为None，则max_features = n_features。注意：在找到至少一个有效的节点样本分区之前，分割的搜索不会停止，即使它需要有效检查多个max_features功能也是如此。

max_leaf_nodes：最大叶子节点数，整数，默认为None

min_impurity_decrease：如果分裂指标的减少量大于该值，则进行分裂。

min_impurity_split：决策树生长的最小纯净度。默认是0。自版本0.19起不推荐使用：不推荐使用min_impurity_split，而建议使用0.19中的min_impurity_decrease。min_impurity_split的默认值在0.23中已从1e-7更改为0，并将在0.25中删除。

bootstrap：是否进行bootstrap操作，bool。默认True。如果bootstrap==True，将每次有放回地随机选取样本，只有在extra-trees中，bootstrap=False

oob_score：是否使用袋外样本来估计泛化精度。默认False。

n_jobs：并行计算数。默认是None。

random_state：控制bootstrap的随机性以及选择样本的随机性。

verbose：在拟合和预测时控制详细程度。默认是0。

warm_start：不常用

class_weight：每个类的权重，可以用字典的形式传入{class_label: weight}。如果选择了“balanced”，则输入的权重为n_samples / (n_classes * np.bincount(y))。

ccp_alpha：将选择成本复杂度最大且小于ccp_alpha的子树。默认情况下，不执行修剪。

max_samples：如果bootstrap为True，则从X抽取以训练每个基本分类器的样本数。如果为None（默认），则抽取X.shape [0]样本。如果为int，则抽取max_samples样本。如果为float，则抽取max_samples * X.shape [0]个样本。因此，max_samples应该在（0，1）中。是0.22版中的新功能。

以datasets里的红酒数据为例，测试代码如下：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from sklearn.model_selection import train_test_split #切分训练集和测试集
from sklearn.ensemble import RandomForestClassifier #导入随机森林模型
from sklearn import tree, datasets

#载入红酒数据
wine = datasets.load_wine()

#只选取前两个特征
X = wine.data[:, :2]
y = wine.target

#拆分训练集和数据集
X_train, X_test, y_train, y_test = train_test_split(X, y)

#设定随机森林中有6颗树
forest = RandomForestClassifier(n_estimators=6, random_state=3)

#拟合数据
forest.fit(X_train, y_train)

#绘制图形
#定义图像中分区的颜色和散点的颜色
cmap_light= ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF'])
cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF'])

#分别用样本的两个特征值创建图像和横轴和纵轴
x_min, x_max = X[:,0].min()-1, X[:,0].max()+1
y_min, y_max = X[:,1].min()-1, X[:,1].max()+1
#用不同的背景色表示不同的类
xx, yy = np.meshgrid(np.arange(x_min, x_max, .02),
                     np.arange(y_min, y_max, .02))
z = forest.predict(np.c_[(xx.ravel(), yy.ravel())]).reshape(xx.shape)

plt.figure()
plt.pcolormesh(xx, yy, z, cmap=cmap_light)

#用散点把样本标出来
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=cmap_bold, edgecolors='k', s=20)
plt.xlim(xx.min(), xx.max())
plt.ylim(yy.min(), yy.max())

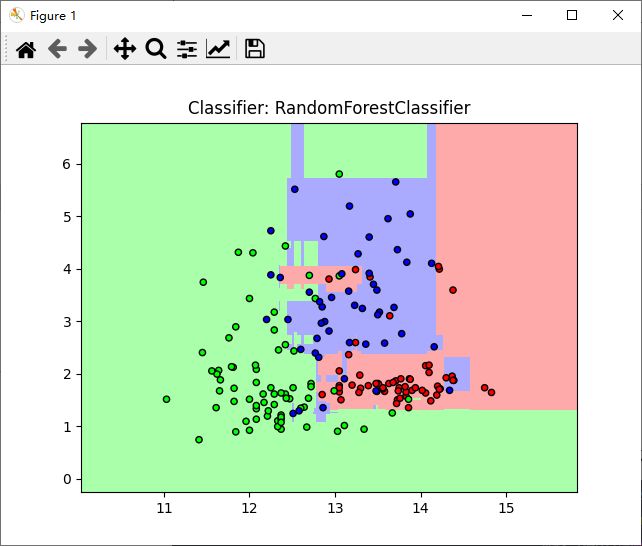
plt.title('Classifier: RandomForestClassifier') #依照参数值修改标题
plt.show()

效果如下：

4.2 RandomForestRegressor随机森林回归

ensemble.RandomForestRegressor函数原型如下：

其中关于决策树的参数：

criterion: “mse”来选择最合适的节点。

splitter: ”best” or “random”(default=”best”)随机选择属性还是选择不纯度最大的属性，建议用默认。

max_features: 选择最适属性时划分的特征不能超过此值。

当为整数时，即最大特征数；当为小数时，训练集特征数*小数；

if “auto”, then max_features=sqrt(n_features).

If “sqrt”, thenmax_features=sqrt(n_features).

If “log2”, thenmax_features=log2(n_features).

If None, then max_features=n_features.

max_depth: (default=None)设置树的最大深度，默认为None，这样建树时，会使每一个叶节点只有一个类别，或是达到min_samples_split。

min_samples_split: 根据属性划分节点时，每个划分最少的样本数。

min_samples_leaf: 叶子节点最少的样本数。

max_leaf_nodes: (default=None)叶子树的最大样本数。

min_weight_fraction_leaf: (default=0) 叶子节点所需要的最小权值

verbose: (default=0) 是否显示任务进程

关于随机森林特有的参数：

n_estimators=10：决策树的个数，越多越好，但是性能就会越差，至少100左右（具体数字忘记从哪里来的了）可以达到可接受的性能和误差率。

bootstrap=True：是否有放回的采样。

oob_score=False：oob（out of band，带外）数据，即：在某次决策树训练中没有被bootstrap选中的数据。多单个模型的参数训练，我们知道可以用 cross validation（cv）来进行，但是特别消耗时间，而且对于随机森林这种情况也没有大的必要，所以就用这个数据对决策树模型进行验证，算是一个简单的交叉验证。性能消耗小，但是效果不错。

n_jobs=1：并行job个数。这个在ensemble算法中非常重要，尤其是bagging（而非boosting，因为boosting的每次迭代之间有影响，所以很难进行并行化），因为可以并行从而提高性能。1=不并行；n：n个并行；-1：CPU有多少core，就启动多少job。

warm_start=False：热启动，决定是否使用上次调用该类的结果然后增加新的。

class_weight=None：各个label的权重。

进行预测可以有几种形式：

predict_proba(x)：给出带有概率值的结果。每个点在所有label的概率和为1.

predict(x)：直接给出预测结果。内部还是调用的predict_proba()，根据概率的结果看哪个类型的预测值最高就是哪个类型。

predict_log_proba(x)：和predict_proba基本上一样，只是把结果给做了log()处理。

测试代码如下：

#随机森林
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
import numpy as np

from sklearn.datasets import load_iris
iris=load_iris()
#print iris#iris的４个属性是：萼片宽度　萼片长度　花瓣宽度　花瓣长度　标签是花的种类：setosa versicolour virginica
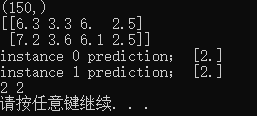
print(iris['target'].shape)
rf=RandomForestRegressor()#这里使用了默认的参数设置
rf.fit(iris.data[:150],iris.target[:150])#进行模型的训练

#随机挑选两个预测不相同的样本
instance=iris.data[[100,109]]
print(instance)
rf.predict(instance[[0]])
print('instance 0 prediction；',rf.predict(instance[[0]]))
print( 'instance 1 prediction；',rf.predict(instance[[1]]))
print(iris.target[100],iris.target[109])

结果如下：

5. 源码仓库地址

图像处理、机器学习的常用算法汇总