DAY28：回溯算法（三）组合总和Ⅲ+电话号码字母组合

216.组合总和Ⅲ

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

• 只使用数字1到9

• 每个数字 最多使用一次

  返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

示例 1:

输入: k = 3, n = 7
输出: [[1,2,4]]
解释:
1 + 2 + 4 = 7
没有其他符合的组合了。

示例 2:

输入: k = 3, n = 9
输出: [[1,2,6], [1,3,5], [2,3,4]]
解释:
1 + 2 + 6 = 9
1 + 3 + 5 = 9
2 + 3 + 4 = 9
没有其他符合的组合了。

示例 3:

输入: k = 4, n = 1
输出: []
解释: 不存在有效的组合。
在[1,9]范围内使用4个不同的数字，我们可以得到的最小和是1+2+3+4 = 10，因为10 > 1，没有有效的组合。

提示:

• 2 <= k <= 9
• 1 <= n <= 60

思路

本题和组合问题的区别就是，组合问题是一共n个数，找到k个数字的所有组合。本题也是找k个数，但是要求这k个数的和是n。

k个数字只能从1–9里面选择。组合问题的n也是限制了1–n的范围。本题相当于在1–9的数字里，选出k个数字的组合，使得其和为n。也就是在组合问题的基础上，加上了和为n的限制！

我们先考虑最简单的k=2,n=4的情况，这种情况下在1–9中选择两个元素令其和=4，就是嵌套两层for循环。当k=3，就是嵌套3层for循环。

当k是n的时候，也就是嵌套n层for循环。此时暴力想法做不出来，就考虑使用回溯。回溯就是用来递归，控制for的嵌套层数。

树形结构

例如k=2 n=4的情况，[1,9]取数字：

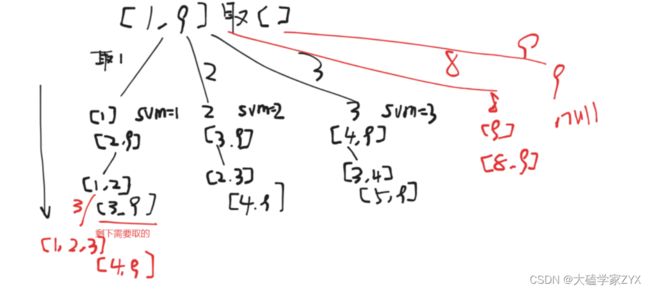
回溯的深度是由K来决定的，k越大，查找深度就越深，因为k越大就要确定越多的数字。K控制了树的深度。

树的宽度是1–9控制的，1–9分出去的分支就是树的宽度。

完整版

• startIndex取i+1，因为组合里不能有重复元素。
• 本题和组合比较像

//此处结果并不需要返回什么，因为结果都存在result里面了
//需要单独定义targetSum和sum，来存放目标和与当前和的数据
//同时还需要定义控制循环开始位置的startIndex！
void backtracking(vector<int>& path,vector<vector<int>>&result,int k,int targetSum,int sum,int startIndex){
    //终止条件
    if(path.size()==k){
        //检查和是否符合要求
        if(sum==targetSum){
            result.push_back(path);
        }
        return;
    }
    
    //单层搜索
    for(int i=startIndex;i<=9;i++){
        //本层累加
        sum = sum+i;
        path.push_back(i);
        //递归for循环，取了[1]之后再取[1,2][1,3][1,4]……
        backtracking(path,result,k,targetSum,sum,i+1);
        //回溯,开始取[2],后面[2,3][2,4]……
        path.pop_back();
        sum = sum-i;
    }

}

//主函数，传参和赋初值可以先写
vector<vector<int>> combinationSum3(int k, int n) {
	int sum=0;
    int startIndex=1;
    vector<int>path;
    vector<vector<int>>result;
    backtracking(path,result,k,n,sum,startIndex);
    return result;
}

debug测试

逻辑错误：没有输出

我们把最开始的版本贴进去之后，发现并没有输出

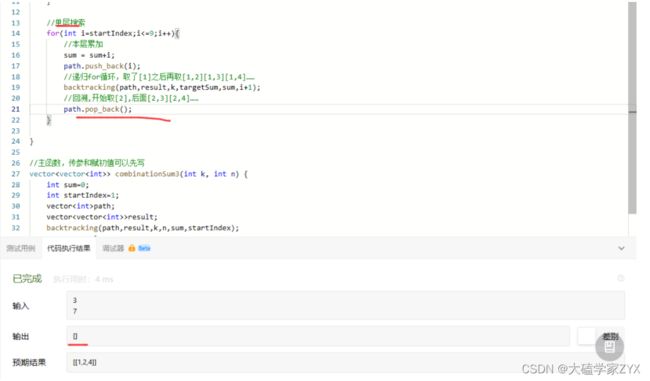
这个问题主要是出在单层搜索的回溯上面。

因为本题是累加sum并且在每一层中判断sum的值是不是等于目标值，因此，sum在每一层都是当前层递归的特定值，必须也进行回溯操作！

没有输出就是因为sum没有回溯，导致1的所有组合计算sum结束了之后，遍历到2的时候，sum值还是在1的所有组合sum基础上进行累加！这使得 sum 的值变得过大，所以 if(sum == targetSum) 条件很难满足，从而使结果集无法被填充。此时如果1中没有符合要求的条件，就不可能有任何输出，因为结果集是空的。

也就是说，不回溯的话只能找得到1开头的符合条件的组合，从2开头起就很难填充结果集了。因为当处理完1开头的所有可能组合之后，sum 的值实际上是1开头的组合的和。

单层逻辑修改为：

• 一定要注意sum也要回溯，这是累加的结果值！

	//单层搜索
    for(int i=startIndex;i<=9;i++){
        //本层累加
        sum = sum+i;
        path.push_back(i);
        //递归for循环，取了[1]之后再取[1,2][1,3][1,4]……
        backtracking(path,result,k,targetSum,sum,i+1);
        //回溯,开始取[2],后面[2,3][2,4]……
        path.pop_back();
        //一定要注意sum也要回溯，这是累加的结果值！
        sum = sum-i;
    }

剪枝操作

本题的剪枝操作和组合有一部分类似，本题是固定在[1,9]内部进行搜索，也可能存在遍历到i，剩下的元素本身已经

也就是剩下的元素 < 还需要加入的元素，9-i+1 < k - path.size()，即为i>9-( k - path.size())+1。

另一个剪枝是关于和sum的剪枝，也就是没到k的情况下，当前数字的sum值如果已经大于targetSum，那么，就不可能存在到了k之后=targetSum的情况了。

剪枝版本

• 剪枝一定要注意剪枝的同时要把回溯做了！

//注意剪枝的同时，直接返回，必须要剪枝同时把回溯也做了
void backtracking(vector<int>& path,vector<vector<int>>&result,int k,int targetSum,int sum,int startIndex){
    //终止条件
    if(path.size()==k){
        //检查和是否符合要求
        if(sum==targetSum){
            result.push_back(path);
        }
        //==k无论如何都会return
        return;
    }
    
    //单层搜索
    for(int i=startIndex;i<=9-(k-path.size())+1;i++){
        //本层累加
        sum = sum+i;
        path.push_back(i);
        
        //如果此时的sum已经比targetSum要大，那么已经可以剪枝去找下一个了
        if(sum>targetSum){
            //剪枝，剪枝的时候一定要记得回溯！
            sum = sum-i;
            path.pop_back();
            //这里最好还是写continue，跳过for循环剩下所有部分进行下一次for循环
            continue;
        }
        
        //递归for循环，取了[1]之后再取[1,2][1,3][1,4]……
        backtracking(path,result,k,targetSum,sum,i+1);
        //回溯,开始取[2],后面[2,3][2,4]……
        path.pop_back();
        sum = sum-i;
    }

}

//主函数，传参和赋初值可以先写
vector<vector<int>> combinationSum3(int k, int n) {
	int sum=0;
    int startIndex=1;
    vector<int>path;
    vector<vector<int>>result;
    backtracking(path,result,k,n,sum,startIndex);
    return result;
}

continue的用法

在C++中，continue语句用于跳过当前循环中剩余的代码，然后直接开始下一次循环。在我们代码这种情况下，continue将跳过当前for循环中 backtracking 函数之后的所有代码（包括回溯操作和sum的恢复），并且立即开始下一次for循环。

这对于剪枝操作是有意义的，因为如果sum已经大于targetSum，那么就没有必要再进一步搜索这个路径了，直接跳过剩下的步骤并尝试下一个可能的数会更有效率。然而，这不意味着可以忽略回溯操作，还是需要在continue之前将path和sum恢复到他们的原始状态，这样才能确保在下一次迭代中path和sum的值是正确的。

但是这道题剪枝操作，一开始把continue写成了return，其实也能过，但是是因为本题的特殊性。最好还是用continue。

(实际上这道题的特性，如果sum已经大于target值了，那么continue再换更大的数字肯定不满足条件，所以直接return也是对的。)

剪枝最后是continue还是return的讨论

使用 return 会直接终止当前的函数调用，回到调用者那里。在这种情况下，return 会终止当前的 backtracking 函数调用，返回到上一层的 backtracking 函数或 combinationSum3 函数。这意味着会直接跳过当前的 for 循环中的其余迭代，可能会错过一些有效的解。

使用 continue 会跳过当前的循环体中的剩余部分，直接开始下一次迭代。在这种情况下，continue 会跳过当前迭代的剩余部分，直接开始下一次迭代。这样，你可以正确地检查所有可能的 i 值，而不会错过任何可能的解。

17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例 1：

输入：digits = "23"
输出：["ad","ae","af","bd","be","bf","cd","ce","cf"]

示例 2：

输入：digits = ""
输出：[]

示例 3：

输入：digits = "2"
输出：["a","b","c"]

提示：

• 0 <= digits.length <= 4
• digits[i] 是范围 ['2', '9'] 的一个数字。

思路

本题需要注意数字对字符串的映射。可以用map做映射也可以用二维数组做映射。

二维数组做映射，就是说数组是字符串类型，数字是对应的下标。下标2对应字符串"abc"，以此类推。

例如输入"23"，比较直观的想法是写两个for循环，一个是2的字符串组合，一个是3的字符串组合，再输出2对应字母和3对应字母的组合。

如果是3个数字，就是3个for循环列出3个对应字母的字符组合。n个for循环，就是回溯来解决。

树形结构

树形结构如下图所示。这棵树的深度是由输入数字的个数来确定的。输入多个数字，就需要在多个数字里面进行选择，每个数字选一个对应字符串里面的字母。

树的宽度是由每个数字对应的字母长度来确定的，比如2对应字母"abc"，树宽度就是abc（三种取值）

伪代码

• backtracking定义的参数一般都是结果集+单个想要的结果！比如path和result
• for循环的嵌套，需要传入startIndex来控制循环起点的一般是在一个集合里面求组合，需要控制这一个集合里面的循环起点避免得到重复组合；而本题是两个集合找元素进行组合，并不需要startIndex来控制之前遍历过哪些元素。
• 但是仍然需要一个index，告诉我们字符串digits中，现在遍历到哪个数字了！方便写终止条件
• 本题是两个集合里面去取元素的组合，不需要控制，直接i=0即可

//先定义收取结果的东西，也就是总结果集vector和单个想要的结果的string
//for循环的嵌套，需要传入startIndex来控制循环起点
void backtracking(string s,vector<string>& result,string digits,int index){
    //终止条件,如果正在遍历的元素到了size，也就是指向末尾了
    //这里不是size()-1！因为最后一个也要处理！
    if(index==digit.size()){
        result.push_back(s);
        return;
    }
    //单层遍历逻辑
    //先取出数字
    int digit = digits[index]-'0';//index表示本层递归取出了哪个数字,注意传入的是字符串"2"的时候，需要减掉'0'，去做下标
    //获取数字对应字符串
    string letters = letterMap[digit];//digit作为下标  本题需要单独写一个letterMap存放对应字符串
    //遍历字符串
    for(int i=0;i<letters.size();i++){
        //加入第一个字母'a'
        s.push_back(letters[i]);
        //隐含index的回溯，递归得到"ad""ae""af"
        backtracking(s,result,digits,index+1);
        //'a'弹出，继续'b'开头
        s.pop_back();
    }
    
}

字符串中的字符’2’转化成int的方法

由于字符串"23"中含有的是字符’2’和’3’，因此我们不能直接对字符进行下标转换，必须将字符转换为int。

注意，字符串中的字符’2’就是可以进行运算的ascii码的形式！

int digit = digits[index]-'0';//此处就是将字符'2'和'3'转化为int 2和3

类似的用法： 有效字母异位词

int record[26]={0}; //注意数组的初始化方式
for(int i=0;i<s.size();i++){ 
     record[s[i]-'a']++; //此处就是将'b'等字符转化成数组下标，0对应a，1对应b
}

类似这样的，数字字符和字母字符和整数之间的转换，以及将其作为数组下标的操作，在处理这类字符串和字符相关的问题中是非常常见的。

将转换后的字符对应的int作为数组或者哈希表的下标，可以用来记录字符的频率和数组中查询字符对应的子集。比如本题，我们使用这个整数作为letterMap数组的下标，查找到对应的字符集。检查频率和下标查找在处理字符串相关的问题中很有用。

字符串字符与int转换补充

在许多编程语言中，字符是用ASCII值来表示的，每个字符都有一个对应的整数。所以可以通过计算字符之间的差值来完成想要的转换。

例如本题，想把字符’2’转化成整数（数组下标）2，那么需要做的是’2’ - ‘0’，因为在ASCII表中，字符’2’的值为50，字符’0’的值为48，他们之间的差值就是2。

同理，如果想把字符’b’转化成数组下标1（假设’a’对应0），需要做的是’b’ - ‘a’，因为在ASCII表中，字符’b’的值为98，字符’a’的值为97，他们之间的差值就是1。

通常来说，如果我们想将数字的字符转为数组下标，我们可以将该字符与’0’的ASCII值做差，这样就可以得到该数字字符对应的整数值。例如，字符’2’转为整数2，可以用’2’ - '0’实现。

类似地，如果我们想将小写字母字符转为一个序列号（假设’a’对应0，‘b’对应1等等），我们可以将该字符与**‘a’**的ASCII值做差，这样就可以得到该字母字符对应的序列号。例如，字符’b’转为整数1，可以用’b’ - 'a’实现。

字符串与字符

在大多数编程语言中，使用单引号（'）括起来的是字符，而使用双引号（"）括起来的是字符串。字符对应一个ASCII值，可以进行数学运算，而字符串则是一系列字符的集合，一般不能直接进行数学运算。

也就是说**"a"表示的就是字符串**！双引号的字符串是不能进行加减运算的，只有单引号的ASCII码可以，例如’a’。

字符串中，'a’表示的是ASCII码的a也就是97，'A’表示的是ASCII码也就是65。

在’A’和’a’之间，除了大小写字母之外，其实还是存在一些符号的！因为65+26 = 91,而’a’的值是97。

在ASCII编码表中，'A’至’Z’的ASCII值是从65至90，'a’至’z’的ASCII值是从97至122。在’Z’（ASCII值90）和’a’（ASCII值97）之间还有6个字符，它们分别是：‘[’（91），‘’（92），‘]’（93），‘^’（94），‘_’（95）和’`'（96）。

完整版

• 注意接收的路径path需要定义成string s而不是vector
• 输入为空的特殊用例，直接加if就行了
• 注意数组定义赋值用的是大括号{}

class Solution {
public:
//注意数组的初始化方式
    string letterMap[10]={
        "", //是逗号不是分号
        "",
        "abc",
        "def",
        "ghi",
        "jkl",
        "mno",
        "pqrs",
        "tuv",
        "wxyz",
    };
    void backtracking(string path,vector<string>&result,int index,string digits){
        //终止条件
        if(path.size()==digits.size()){
            result.push_back(path);
            return;
        }
        //单层搜索,先得到第一个遍历的数字
        int digitsNum = digits[index]-'0';
        //第一个遍历的数字的字符串
        string a = letterMap[digitsNum];
        for(int i=0;i<a.size();i++){
            path.push_back(a[i]);
            backtracking(path,result,index+1,digits);
            //递归收集'a'开头结束之后，去找'b'开头
            path.pop_back();//pop里面没有参数，error: too many arguments to function call, expected 0, have 1
        }
    }
    vector<string> letterCombinations(string digits) {
        int index=0;
        vector<string>result;
        string path;
        if(digits.size()==0){
            return result;
        }
        backtracking(path,result,index,digits);
        return result;
    }
};

补充：为啥这里不考虑剪枝

电话号码这道题其实并不算组合问题。组合型问题，就是可以剪枝优化的。但是子集型问题很难剪枝，电话号码这道题实际上是子集型问题，并不是组合型问题。