哈希表(模拟散列表 字符串哈希)
目录
- 一、哈希表的概念
- 二、模拟散列表
-
- 题目
- 代码实现
-
- ①拉链法
- ②开放寻址法
- 三、字符串哈希
-
- 题目
- 思路
- 注意点
- 代码实现
一、哈希表的概念
哈希表(又称为散列表),将一个比较大的值域映射到一个小的范围。
例如有哈希函数 h(x),将区间 [ − 1 0 9 , 1 0 9 ] [-10^9,10^9] [−109,109]的数字映射到 [ 0 , 1 0 5 ] [0,10^5] [0,105]中。
方法:直接将 x x x m o d mod mod 1 0 5 10^5 105,但是这样会存在哈希冲突。
(冲突:两个数映射成了同一个数。)
( 取 模 的 数 尽 可 能 是 质 数 且 与 2 的 整 次 幂 尽 量 远 ) \color{red}{(取模的数尽可能是质数且与2的整次幂尽量远)} (取模的数尽可能是质数且与2的整次幂尽量远)
(取质数是发生冲突概率最小的方法)
解决哈希冲突的方法:①开放寻址法 ②拉链法
类似于离散化,离散化保序,而哈希表不保序。离散化是一种极其特殊的Hash方式。
一般的操作有:
- 插入
- 查找
- 删除(算法题中一般不用)(通过给对应数打标记来实现)
哈希表的时间复杂度如下:
-
插入(Insertion) 操作的平均时间复杂度是 O ( 1 ) O(1) O(1)。在理想情况下,插入一个元素到哈希表中只需要常数时间。然而,在发生哈希冲突(Hash Collision)时,需要处理冲突,可能会导致插入操作的时间复杂度略微增加,但仍然是常数时间的。
-
查找(Lookup) 操作的平均时间复杂度是 O ( 1 ) O(1) O(1)。通过哈希函数计算出元素的哈希值,然后在哈希表中进行查找。在理想情况下,查找操作只需要常数时间。然而,如果存在哈希冲突,可能需要遍历哈希表中的某个桶(Bucket)来寻找目标元素,但由于哈希表的设计,这个遍历的代价也是常数时间的。
-
删除(Deletion) 操作的平均时间复杂度是 O ( 1 ) O(1) O(1)。类似于插入和查找操作,在理想情况下,删除操作只需要常数时间。即使存在哈希冲突,也可以通过哈希函数计算出目标元素的位置,并进行删除。
需要注意的是,以上时间复杂度是基于平均情况的估计。在极端情况下,例如哈希函数设计不当或者存在大量的哈希冲突,哈希表的性能可能会下降,导致插入、查找和删除操作的时间复杂度接近O(n),其中n是哈希表中存储的元素数量。
二、模拟散列表
题目
题目描述:
维护一个集合,支持如下几种操作:
I x,插入一个数x;Q x,询问数x是否在集合中出现过;
现在要进行 n n n 次操作,对于每个询问操作输出对应的结果。
输入格式:
第一行包含整数 n n n,表示操作数量。
接下来 n n n 行,每行包含一个操作指令,操作指令为I x,Q x中的一种。
输出格式:
对于每个询问指令Q x,输出一个询问结果,如果 x 在集合中出现过,则输出 Yes,否则输出 No。
每个结果占一行。
数据范围:
1 ≤ n ≤ 1 0 5 1≤n≤10^5 1≤n≤105
− 1 0 9 ≤ a ≤ 1 0 9 -10^9≤a≤10^9 −109≤a≤109
输入样例:
5
I 1
I 2
I 3
Q 2
Q 5
输出样例:
Yes
No
代码实现
①拉链法
每个下列吊着的链表可以看作常数个,因此查询的时间复杂度大大降低。
#define _CRT_SECURE_NO_WARNINGS
#include②开放寻址法
数组通常开到题目要求的数量的2~3倍(依旧找到对应的质数)
其原理相当于用空间换时间:要解决大量冲突会很费时间,开2~3倍可以减少冲突。
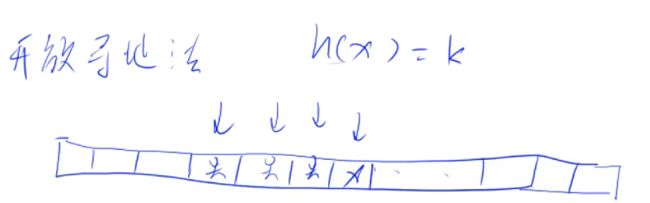
找到数组上对应的位置后,检测有没有被占用,有的话往后找位置放。
#define _CRT_SECURE_NO_WARNINGS
#include三、字符串哈希
题目
题目描述:
给定一个长度为 n n n 的字符串,再给定 m m m 个询问,每个询问包含四个整数 l 1 , r 1 , l 2 , r 2 l_1,r_1,l_2,r_2 l1,r1,l2,r2,请你判断 [ l 1 , r 1 ] [l_1,r_1] [l1,r1] 和 [ l 2 , r 2 ] [l_2,r_2] [l2,r2] 这两个区间所包含的字符串子串是否完全相同。
字符串中只包含大小写英文字母和数字。
输入格式:
第一行包含整数 n n n 和 m m m,表示字符串长度和询问次数。
第二行包含一个长度为 n n n 的字符串,字符串中只包含大小写英文字母和数字。
接下来 m m m 行,每行包含四个整数 l 1 , r 1 , l 2 , r 2 l_1,r_1,l_2,r_2 l1,r1,l2,r2,表示一次询问所涉及的两个区间。
注意,字符串的位置从 1 1 1 开始编号。
输出格式:
对于每个询问输出一个结果,如果两个字符串子串完全相同则输出 Yes,否则输出 No。
每个结果占一行。
数据范围:
1 ≤ n ≤ 1 0 5 1≤n≤10^5 1≤n≤105
1 ≤ m ≤ 1 0 5 1≤m≤10^5 1≤m≤105
输入样例:
8 3
aabbaabb
1 3 5 7
1 3 6 8
1 2 1 2
输出样例:
Yes
No
Yes
思路
字符串哈希 O ( n + m ) O(n+m) O(n+m)
全称 字符串前缀哈希法,把字符串变成一个 p p p 进制数字**(哈希值)**,实现不同的字符串映射到不同的数字。并且,用 h [ N ] h[N] h[N] 记录字符串前 N N N 个字符的 hash 值,类似于前缀和。
作用就是把 O ( N ) O(N) O(N) 的时间复杂度降为 O ( 1 ) O(1) O(1)。比如本题就是对比任意两段内字符串是不是相同,正常就是类似于一个循环长度次的substr,其实用hash 差就能一步搞定。
例如:
str = "ABCABCDEYXCACWING";
h[0] = 0;
h[1] = "A"的Hash值;
h[2] = "AB"的Hash值;
h[3] = "ABC"的Hash值;
h[4] = "ABCA"的Hash值;
对形如 X 1 , X 2 , X 3 , . . . , X n − 1 , X n X_1,X_2,X_3,...,X_{n−1},X_n X1,X2,X3,...,Xn−1,Xn的字符串,采用字符 A S C I I ASCII ASCII码乘上 P P P 次方来计算哈希值。
映射公式: ( X 1 × P n − 1 + X 2 × P n − 2 + . . . + X n − 1 × P 1 + X n × P 0 ) (X_1×P^{n−1} + X_2 × P^{n−2}+...+X_{n−1} × P^1+X_n×P^0) (X1×Pn−1+X2×Pn−2+...+Xn−1×P1+Xn×P0) m o d mod mod Q Q Q
例如:
字符串 A B C D ABCD ABCD, P = 131 P=131 P=131
那么 h [ 4 ] = 65 ∗ 13 1 3 + 66 ∗ 13 1 2 + 67 ∗ 13 1 1 + 68 ∗ 13 1 0 h[4]=65∗131^3+66∗131^2+67∗131^1+68∗131^0 h[4]=65∗1313+66∗1312+67∗1311+68∗1310
而 A B AB AB, P = 131 P=131 P=131
说是 h [ 2 ] = 65 ∗ 13 1 1 + 66 ∗ 13 1 0 h[2]=65∗131^1+66∗131^0 h[2]=65∗1311+66∗1310
我们想要求 C D CD CD 的 h a s h hash hash值,怎么求呢?
就是 h [ 4 ] − h [ 2 ] ∗ 13 1 2 h[4]−h[2]∗131^2 h[4]−h[2]∗1312(意义在于将 h [ 4 h[4 h[4] 与 h [ 2 ] h[2] h[2] 的字符串对齐再相减)
构建: h [ i ] = h [ i − 1 ] × P + s [ i − 1 ] , i ∈ [ 1 , n ] h[i]=h[i−1]×P+s[i−1],i∈[1,n] h[i]=h[i−1]×P+s[i−1],i∈[1,n],其中 h h h为前缀和数组, s [ i − 1 ] s[i−1] s[i−1]为字符串数组此位置字符对应的ASCII码。
应用: 查询 l , r l,r l,r 之间部分字符串的 h a s h = h [ r ] − h [ l − 1 ] × P r − l + 1 hash=h[r]−h[l−1]×P^{r−l+1} hash=h[r]−h[l−1]×Pr−l+1
注意点
- 任意字符不可以映射成 0 0 0,否则会出现不同的字符串都映射成0的情况,比如: A A A, A A AA AA, A A A AAA AAA 皆为 0 0 0。
- 冲突问题:通过巧妙(经验)设置 P = 131 或 13331 P = 131 或 13331 P=131或13331, Q = 2 64 Q = 2^{64} Q=264,一般可以理解为不产生冲突(99.99%概率不冲突)。
unsigned long long的数值范围正好为 0 0 0 ~ 2 64 − 1 2^{64}-1 264−1,所以可以直接采用unsigned来接收数字,由于二进制的溢出特性,当unsigned long long下的最高位的进位 1 1 1 溢出之后相当于除以 2 64 2^{64} 264。
代码实现
#define _CRT_SECURE_NO_WARNINGS
#include
