【博弈论笔记】第五章 完全但不完美信息动态博弈
文章目录
- 第五章 完全但不完美信息动态博弈
-
- 5.1 不完美信息动态博弈
-
- 5.1.1 相关概念
- 5.1.2 不完美信息动态博弈的表示
- 5.1.3 不完美信息动态博弈的子博弈
- 5.2 完美贝叶斯均衡
-
- 5.2.1 完美贝叶斯均衡的定义
- 5.2.2 关于判断形成的进一步理解
- 5.3 单一价格二手车博弈模型
-
- 5.3.1 单一价格二手车交易模型
- 5.3.2 均衡的类型
- 5.3.3 模型的**纯策略**完美贝叶斯均衡
- 5.3.4 模型的混合策略完美贝叶斯均衡
- 5.3.5 市场类型归纳总结
- 5.4 双价二手车交易博弈
- Summary
此部分博弈论笔记参考自经济博弈论(第四版)/谢识予和老师的PPT,是在平时学习中以及期末备考中整理的,主要注重对本章节知识点的梳理以及重点知识的理解,细节和逻辑部分还不是很完善,可能不太适合初学者阅读(看书应该会理解的更明白O(∩_∩)O哈哈~)。现更新到博客上供大家浏览,希望能够帮助到正在学习博弈论的大家。
第五章 完全但不完美信息动态博弈
5.1 不完美信息动态博弈
5.1.1 相关概念
-
博弈信息局限
- 不完全信息:博弈方在得益信息方面不对称。存在于静态博弈和动态博弈中
- 不完美信息:博弈方在博弈进程信息方面不对称。 只存在于动态博弈
-
完美信息
动态博弈中,如果后行动的博弈方在自己行动之前,可观察到先前博弈的进程,那么有关于前面阶段博弈进程的充分信息,就称为有“完美信息"( perfectinformation)。 -
完全但不完美信息动态博弈
各博弈方对得益情况有“完全信息”,但对博弈进程的没有充分信息的动态博弈, 称为“完全但不完美信息动态博弈”,简称“不完美信息动态博弈”。
5.1.2 不完美信息动态博弈的表示
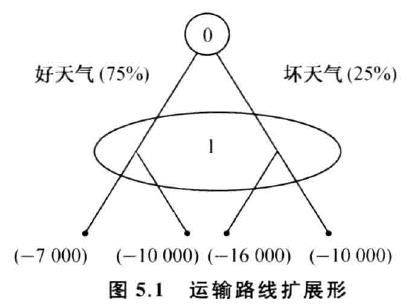
买方2无法知道前两阶段的路径:“好——卖”? “差——卖”?
对此例进行数值分析:
- 对于卖方而言,要价2千,车况好时正常卖,车况差时需花1千修理伪装再卖。卖不出去就白白损失1千。
- 对于买方而言,车况好对买方值3千,车况差值1千
这种情况下,博弈方的策略、信息和判断间存在复杂的交互决定关系,正是不完美信息动态博弈的研究对象。
5.1.3 不完美信息动态博弈的子博弈
对这种博弈类型的子博弈进行定义:
要求:
-
原博弈不是自己的一个子博弈
-
包含所有在初始节点之后的选择节点和终点,但不包含不跟在此初始节点之后的节点
-
不分割任何信息集:子博弈必须从一个单节点信息集开始
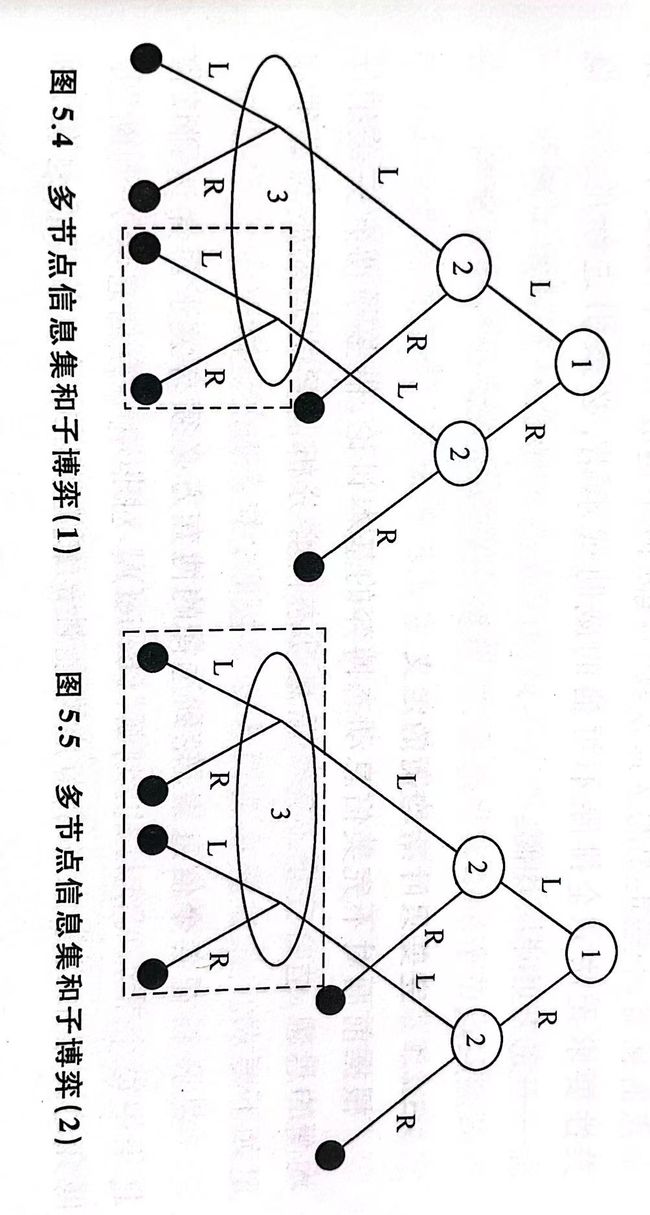
图5.4和图5.5都不是子博弈,因为5.4分割了信息集,5.5未从单节点开始
5.2 完美贝叶斯均衡
5.2.1 完美贝叶斯均衡的定义
均衡对任何种类的博弈分析都是关键,对不完美信息动态博弈也不例外。对于一个动态博弈来讲,可信性则始终是均衡的中心问题,理想的均衡必须排除任何不可信的威胁或承诺。
在完全且完美信息动态博弈中,通过要求均衡策略组合满足子博弈完美性,以保证均衡策略中没有不可信的威胁或承诺。
在完全但不完美信息的动态博恋中, 因为存在多节点信息集, 一些重要的选择及其后续阶段不构成子博弈,因此子博弈完美性要求无法完全排除不可信的威胁或承诺, 必须引进新的均衡概念——完美贝叶斯均衡。
结合此图来说明完美贝叶斯均衡的要求:

-
要求1:概率判断:在各信息集处,选择的博弈方须具有对博弈到达该信息集中每个节点可能性的“判断”
其中,多节点信息集处的“判断”是博弈到达该信息集中各个节点的概率分布;单节点信息集处的“判断”是博弈到达该节点的概率为1。
例如若判断博弈方1选L的概率大——》 博弈方2选U;若判断博弈方1选M的概率大——》 博弈方2选D。博弈方2的判断是决策的必要基础。
要求 1 实际上就是前面提到的解决不完美信息动态博弈的基本前提, 在多节点信息集处轮到选择的博弈方, 必须对其中每个节点达到的可能性大小有基本判断, 否则决策会失去根据,也不可能存在策略的稳定性,更谈不上均衡。
-
要求2:序列理性:给定各博弈方的“判断”,他们的策略必须是“序列理性” 的
要求 2 的序列理性在子博弈中就是子博弈完美性,在多节点信息集开始的不构成子博弈的部分中,通过要求各博弈方遵守最大利益原则排除策略中不可信的威胁或诺言。
要求 2 也是非常必要的。本例中如果没有这个要求, 只要求满足纳什均衡和子博弈完美性, 博弈方 2 有一个可为自己争取到最大利益 3 , 但 包含不可信威胁的均衡策略,那就是博弈方 2 威胁在轮到自己选择时将 唯一地只选 D。如果博弈方 2 采取这个策略, 博亦方 1 的最佳对策是第 一阶段直接选择 R \mathrm{R} R 结束博弈, 双方得益是 ( 1 , 3 ) (1,3) (1,3) 。
上述策略组合显然是 一个纳什均衡, 由于本博弈没有子博弈, 子博弈完美性要求自动满足, 它也是子博弈完美纳什均衡。
但是博弈方 2 在博弈方 1 不选 R \mathrm{R} R 的情况下 只选 D, 在博弈方 1 选 L \mathrm{L} L 的概率很大时明显是不可信的威胁, 因为博弈方 2 选 D 的期望得益比选 U 小得多, 不符合最大利益原则。
-
要求3:均衡路径上的判断符合均衡策略:在均衡路径上的信息集处, “判断”由贝叶斯法则和各博弈方的均衡策略决定。
-
要求4:非均衡路径上判断符合均衡策略:不在均衡路径上的信息集处,“判断”也必须符合各方均
衡策略。不完美信息博弈中存在多节点信息集,博弈过程中至少部分博弈方在部分信息集无法确定前面的博弈路径。“在均衡路径上”的信息集, 意味着如果博弈按照均衡策略进行,该信息集会以正概率达到; “不在均衡路径上”的信息集, 意味着博弈按均衡策略进行时, 达到的概率为0。
要注意“判断”和“策略”是否矛盾
5.2.2 关于判断形成的进一步理解
-
二手车交易模型
分析:
(1) 汽车本身好、差的概率: p ( g ) 、 p ( b ) , p ( g ) + p ( b ) = 1 p(g) 、 p(b), p(g)+p(b)=1 p(g)、p(b),p(g)+p(b)=1
(2) 博弈方1选卖后, 车况好、差的概率: p ( g ∣ s ) 、 p ( b ∣ s ) p(g \mid s) 、 p(b \mid s) p(g∣s)、p(b∣s), p ( g ∣ s ) + p ( b ∣ s ) = 1 p(g \mid s)+p(b \mid s)=1 p(g∣s)+p(b∣s)=1 。(3) 假设: 已知卖方在车况好、差时选择卖或不卖的概率:
车况好: p ( s ∣ g ) 、 1 − p ( s ∣ g ) p(s \mid g) 、 1-p(s \mid g) p(s∣g)、1−p(s∣g)
车况差: p ( s ∣ b ) 、 1 − p ( s ∣ b ) p(\mathbf{s} \mid \mathbf{b}) 、 1 - p(\mathbf{s} \mid \mathbf{b}) p(s∣b)、1−p(s∣b)买方要做出判断:
p ( g ∣ s ) = p ( g ) ⋅ p ( s ∣ g ) p ( s ) = p ( g ) ⋅ p ( s ∣ g ) p ( g ) ⋅ p ( s ∣ g ) + p ( b ) ⋅ p ( s ∣ b ) \begin{aligned} p(g \mid s) & =\frac{p(g) \cdot p(s \mid g)}{p(s)} \\ & =\frac{p(g) \cdot p(s \mid g)}{p(g) \cdot p(s \mid g)+p(b) \cdot p(s \mid b)} \end{aligned} p(g∣s)=p(s)p(g)⋅p(s∣g)=p(g)⋅p(s∣g)+p(b)⋅p(s∣b)p(g)⋅p(s∣g)
数值例子:(1) 车况好、差的概率: p ( g ) = p ( b ) = 0.5 p(g)=p(b)=0.5 p(g)=p(b)=0.5
(2) 卖方的策略选择:
A. 车况好 卖方一定卖 : p ( s ∣ g ) = 1 \mathrm{p}(\mathrm{s} \mid \mathrm{g})=1 p(s∣g)=1
B. 车况差需斟酌:买方买的概率(即买方的策略选择)
假设:买方买的概率 0.5
卖方卖的期望得益: 0.5 × 1 + 0.5 × ( − 1 ) = 0 = 0.5 \times 1+0.5 \times(-1)=0= 0.5×1+0.5×(−1)=0= 不卖的得益(3)卖方的判断:混合策略 p ( s ∣ b ) = 0.5 p(s|b)=0.5 p(s∣b)=0.5符合卖方的均衡策略,也符合买方自己的均衡策略
(4)买方的判断:
p ( g ∣ s ) = 0.5 × 1 0.5 × 1 + 0.5 × 0.5 = 0.5 0.75 = 2 3 , p ( b ∣ s ) = 1 − p ( g ∣ s ) = 1 − 2 / 3 = 1 / 3 p(g \mid s) =\frac{0.5 \times 1}{0.5 \times 1+0.5 \times 0.5}=\frac{0.5}{0.75}=\frac{2}{3},p(b \mid s)=1-p(g \mid s)=1-2 / 3=1 / 3 p(g∣s)=0.5×1+0.5×0.50.5×1=0.750.5=32,p(b∣s)=1−p(g∣s)=1−2/3=1/3
在卖方的策略[p(s|g)=1, p(s|b)=0.5]下,买方的信息集有较大概率会达到,因此是在“均衡路径上的信息集” 。买方的“判断”是 满足要求3的判断。 -
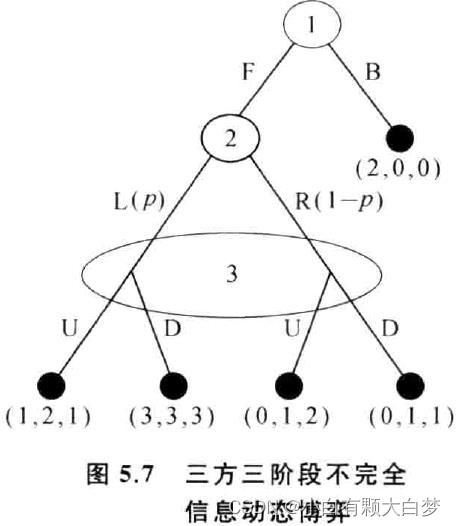
三方三阶段不完全信息动态博弈
逆推归纳法:
对于博弈方3:选U的期望为 1 ∗ p + ( 1 − p ) ∗ 2 = 2 − p 1*p+(1-p)*2=2-p 1∗p+(1−p)∗2=2−p,选D的期望为 3 ∗ p + ( 1 − p ) ∗ 1 = 1 + 2 p 3*p+(1-p)*1=1+2p 3∗p+(1−p)∗1=1+2p,所以 p = 1 / 3 p=1/3 p=1/3是临界条件
对于博弈方2:L策略是严格上策,一定选L
对于博弈方1:知道2选L,之后3会选D,所以它一定选F
此过程中,博弈方3“判断”为p=1 ,与博弈方2选L这个策略相符,所以满足要求3,又因为非均衡路径上无信息集,所以要求4自动满足,所以上述方案是完美贝叶斯均衡
另一个例子
如果是策略(B,L,U)及“判断” p=0
首先, 该策略组合是一个纳什均衡。事实上当博弈方 1 选择 B \mathrm{B} B 后, 其他两博弈方根本没有选择机会。而对博弈方 1 来说,如果其他两博弈方的策略是 ( L , U ) (\mathrm{L}, \mathrm{U}) (L,U), 当然选 B 最合算。其次, 当博弈方 3 对博弈方 2 选择的“判断” p = 0 p=0 p=0 时, (B, L, U) 是序列理性的。第三, 因为均衡路 径上没有需要判断的信息集, 要求 3 自动满足。也就是说, 策略组合 (B, L, U) 和博弈方 3 的 “判断” p = 0 p=0 p=0 满足完美贝叶斯均衡的要求 1 − 3 。 1-3 。 1−3。
但对于要求4而言,博弈方3 “判断” p=0与博弈方2的策略L不符——不满足要求4
所以(B,L,U)不是完美贝叶斯均衡
5.3 单一价格二手车博弈模型
二手车交易正是不完美信息动态博弈问题的典型代表,搞清二手车交易中的博弈关系及其各种均衡,可以对此类博弈问题有更深刻的理解为此类问题的建摸和分析提供更多思路。
本章后面部分主要以二手车交易作为例子进行分析。二手车交易有多种不同的情况,如价格是否有选择性、是否允许讨价还价、买方发觉受骗时是否可以向卖方追究责任索取赔偿等,不同情况的博弈模型肯定是有差异的。本节讨论已多次提到的单一价格模型,后面两节进一步讨论价格有高低的双价模型,以及有退款保证的模型。
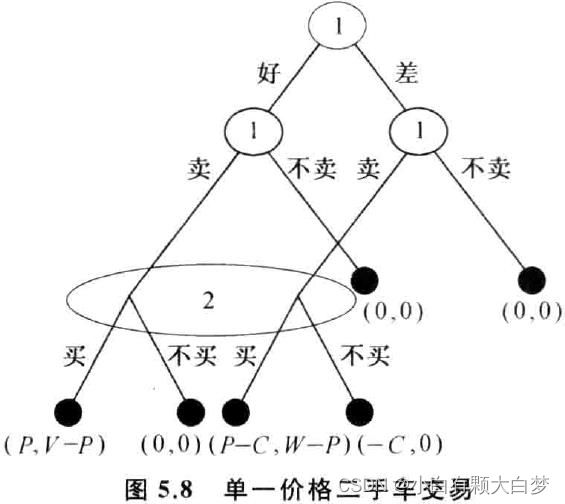
5.3.1 单一价格二手车交易模型
图上的字母代表了不同情况下的得益:车况好、差对买方的价值:V, W,卖方卖价:P,伪装成本:C
假设① 车价大于伪装成本: P>C ② 车况好价值大于价格: V>P ③ 车况差价值小于价格: W 简要分析 在分析二手车交易模型时先引入均衡的类型概念。 根据效率差异分类 合并均衡和分开均衡 合并均衡 ( pooling equilibrium):市场均衡中,所有有完美信息的卖方,不管商品是好是差,都采用相同策略 例如: 分开均衡 ( separating equilibrium):市场均衡中,拥有商品质量不同的卖方会采取完全不同的策略 例如: ① 合并均衡中卖方的行为不能反映任何有用信息,买方“判断”时,可忽略其行为。 ③ 混成均衡中卖方行为能给买方提供一定的信息,但不足以让买方得出肯定的“判断”,只能得到一个概率分布的“判断”。 市场部分成功的完美贝叶斯均衡 若差车出现的概率 p b p_b pb很小,且伪装成本 C C C相对于车价 P P P很小,则下列策略组合和判断组成为完美贝叶斯均衡: 分析: (1) 买方策略 (2) 卖方策略 此时买方的判断: p ( g ∣ s ) = p g , p ( b ∣ s ) = p b \mathbf{p}(\mathrm{g} \mid \mathbf{s})=\mathbf{p}_{\mathrm{g}}, \mathbf{p}(\mathbf{b} \mid \mathbf{s})=\mathbf{p}_{\mathbf{b}} p(g∣s)=pg,p(b∣s)=pb与卖方策略相符合。 (3)完美贝叶斯均衡判断 要求 1: 存在概率判断 [ p ( g ∣ s ) = p g , p ( b ∣ s ) = p b ] \left[p(g \mid s)=p_g, p(b \mid s)=p_b\right] [p(g∣s)=pg,p(b∣s)=pb] 要求4: 非均衡路径上判断也须符合均衡策略 无非均衡路径上的信息集 以上四个条件都满足,所以上述策略是市场部分成功时的完美贝叶斯均衡 市场完全成功(分开均衡)的完美贝叶斯均衡 若:差车出现的概率Pb很小,但伪装成本C >P,则下列策略组合和判断组成为完美贝叶斯均衡 分析: (1) 买方策略 (2) 卖方策略 (3)买方判断 p ( g ∣ s ) = 1 , p ( b ∣ s ) = 0 p(g \mid s)=1, \quad p(b \mid s)=0 p(g∣s)=1,p(b∣s)=0 (4)完美贝叶斯均衡判断 双方策略都满足序列理性的要求。也不难看出, 在均衡路径上 信息集的买方判断符合双方的均衡策略和贝叶斯法则, 同时不存在不在 均衡路径上需要判断的信息集。这就证明了上述策略组合和判断构成了 完美贝叶斯均衡。 市场完全失败(合并均衡) 的完美贝叶斯均衡 如果出现最悲观的情况,即买方根据以往经验,判断卖方选择卖时一定车况差,则下列策略组合和判断组成为完美贝叶斯均衡: 分析: (1)买方策略 买的期望得益: 0× (V-P)+1× (W-P)=W-P <0——》 不买 (2)卖方策略 车好——》 卖的得益 =0——》 不卖 满足完美贝叶斯均衡的要求1-4 前面三种类型的市场都可以用纯策略来解决,还剩下一种市场部分失败的类型 市场接近失败的基本特征: (1) P > C P>C P>C时差车的卖方才会卖车; 这种情况下,如果双方策略都限于纯策略,买方只能不买,卖方也只好不卖,市场完全失败,只有采用混合策略才能避免这样的结果。 数值例子: 假设$① V=3000 ② W=0③ P=2000④ C=1000⑤ p_g=p_b=0.5 $ 此时经验证满足市场接近失败的两个条件。 策略和判断 完美贝叶斯均衡判断 要求1:存在概率判断: p ( g ∣ s ) = 2 / 3 , p ( b ∣ s ) = 1 / 3 p(g \mid s)=2 / 3, p(b \mid s)=1 / 3 p(g∣s)=2/3,p(b∣s)=1/3 要求 3 : 买方的判断是否符合卖方策略和贝叶斯法则? 要求2:序列理性 综上所述,双方策略组合与买方判断构成完美贝叶斯均衡。 车况有好坏两种情况,在这两种情况下都可能以高价或低价卖出。 基本假设: 分析 仅针对市场完全成功下双方策略组合与判断进行讨论: 完美贝叶斯均衡证明 (1)买方的策略选择 (2)卖方的策略选择 (3)买方的判断 结论:上述策略组合和判断通过完美贝叶斯均衡的检验 对于其他情况,如果C趋近于0,那么 p g ( V − P h ) + p b ( W − P h ) < 0 \mathbf{p}_{\mathrm{g}}\left(\mathbf{V}-\mathbf{P}_{\mathrm{h}}\right)+\mathbf{p}_{\mathrm{b}}\left(\mathbf{W}-\mathbf{P}_{\mathrm{h}}\right)<0 pg(V−Ph)+pb(W−Ph)<0 即买方选买期望得益小于 0 , 则买方的必然选择是不买, 而卖方当然就卖 不出去。这样市场就完全痽痪了, 卖方只好全部退出市场, 质量好的商品也没有人相信购买。这种在信息不完美的情况下, 劣质品赶走优质品, 搞垮整个市场的机制, 最先由乔治 - 阿克罗夫 (George Akerlof) 在讨论柠檬市场交易问题时提出, 称为“柠檬原理”。 基本概念 完美贝叶斯均衡 单一价格二手车博弈模型 双价二手车交易:只讲了市场完全成功的一个例子
① 双方积极选择都有风险
② 保守选择会丧失潜在利益
③ 双方无绝对上策
④ 博弈结果有许多种可能5.3.2 均衡的类型
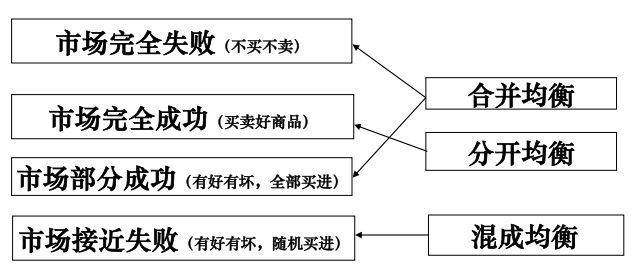
② 分开均衡中卖方的行为完全反映商品质量,能给买方“判断”提供依据。5.3.3 模型的纯策略完美贝叶斯均衡
买的期望得益: p g ( V − P ) + p b ( W − P ) p_g(V-P)+p_b(W-P) pg(V−P)+pb(W−P),而 V > P > W , p b \mathbf{V}>\mathbf{P}>\mathbf{W}, \mathbf{p}_{\mathbf{b}} V>P>W,pb 很小 ⟶ \longrightarrow ⟶ 期望得益 > 0 ⟶ >\mathbf{0}\longrightarrow >0⟶ 买方选买
卖方清楚买方的判断, 知道一定能卖出。
要求 2 : 序列理性,遵守最大利益原则同时无不可信的行为或威胁
要求3: 均衡路径上的信息集判断符合均衡策略:
买的期望得益: 1 × ( V − P ) + 0 × ( W − P ) = V − P > 0 1 \times(\mathrm{V}-\mathrm{P})+0 \times(\mathrm{W}-\mathrm{P})=\mathrm{V}-\mathrm{P}>0 1×(V−P)+0×(W−P)=V−P>0 ⟶ \longrightarrow ⟶ 一定买
车好 ⟶ \longrightarrow ⟶ 卖的得益 P > 0 ⟶ \mathrm{P}>\mathbf{0}\longrightarrow P>0⟶ 卖
车差 ⟶ \longrightarrow ⟶ 卖的得益 P − C < 0 \mathbf{P}-\mathbf{C}<\mathbf{0} P−C<0 ⟶ \longrightarrow ⟶ 不卖
车差——》 卖的得益 = - C< 0——》 不卖5.3.4 模型的混合策略完美贝叶斯均衡
(2) 买方买车的期望得益 < 0 <0 <0即 p ( g ) ( V − P ) + p ( b ) ( W − P ) < 0 p(g)(V-P)+p(b)(W-P)<0 p(g)(V−P)+p(b)(W−P)<0
这里的混合策略,即差车的卖方以一定概率随机选择卖还是不卖,如车的卖方选择卖,而买方也以一定的概率随机选择买还是不买。如果这是一个均衡,则正是市场接近失败类型的均衡。
A. 卖方:车况好, 卖; 车况差, 0.5 的概率随机卖或不卖
B. 买方: 0.5 的概率随机买或不买
C. 买方判断: p ( g ∣ s ) = 2 / 3 , p ( b ∣ s ) = 1 / 3 p(g \mid s)=2 / 3, p(b \mid s)=1 / 3 p(g∣s)=2/3,p(b∣s)=1/3
已知 : p g = p b = 0.5 , p ( s ∣ g ) = 1 , p ( s ∣ b ) = 0.5 \mathrm{p}_{\mathrm{g}}=\mathrm{p}_{\mathrm{b}}=0.5, \mathrm{p}(\mathrm{s} \mid \mathrm{g})=1, \mathrm{p}(\mathrm{s} \mid \mathrm{b})=0.5 pg=pb=0.5,p(s∣g)=1,p(s∣b)=0.5
卖方选卖情况下车况好的概率
p ( g ∣ s ) = p g ⋅ p ( s ∣ g ) p g ⋅ p ( s ∣ g ) + p b ⋅ p ( s ∣ b ) = 0.5 × 1 0.5 × 1 + 0.5 × 0.5 = 0.5 0.75 = 2 3 p(g \mid s) =\frac{p_g \cdot p(s \mid g)}{p_g \cdot p(s \mid g)+p_b \cdot p(s \mid b)} =\frac{0.5 \times 1}{0.5 \times 1+0.5 \times 0.5}=\frac{0.5}{0.75}=\frac{2}{3} p(g∣s)=pg⋅p(s∣g)+pb⋅p(s∣b)pg⋅p(s∣g)=0.5×1+0.5×0.50.5×1=0.750.5=32
与买方的判断一致
5.3.5 市场类型归纳总结
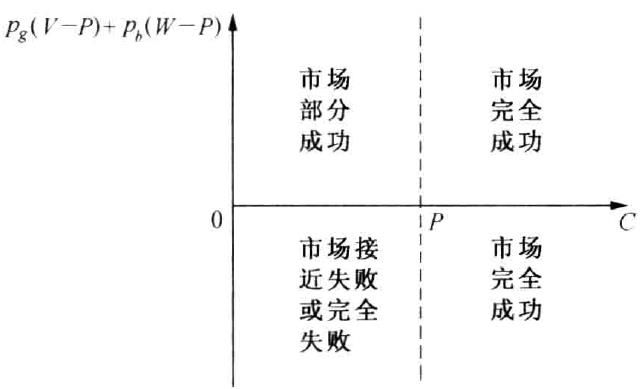
5.4 双价二手车交易博弈

买方判断与卖方策略一致。
同时这种情况也是该模型的唯一完美贝叶斯均衡——市场完全成功型分开均衡Summary