Nova: Recursive Zero-Knowledge Arguments from Folding Schemes学习笔记

1. 引言

前序博客有：

• Lurk——Recursive zk-SNARKs编程语言
• rank-1 constraint system R1CS
• Spartan中 Vitalik R1CS例子 SNARK证明基本思路

微软团队2021年论文 《Nova: Recursive Zero-Knowledge Arguments from Folding Schemes》。
开源代码见：

• https://github.com/Microsoft/Nova（Rust）

---

作者视频讲解见：

• 2022年2月 Nova: Recursive Zero-Knowledge Arguments from Folding Schemes - Srinath Setty

Nova为：

• a SNARK for iterative computations：用于证明$y=F(F(F(F(F(x)))))$，其中：
  • $F$为（potentially non-deterministic）computation
  • $x$为输入，$y$为输出

Nova这样的iterative computation SNARK的应用场景有：

• VDFs：此时$F$为某delay function，如MinRoot，计算某有限域内的cube root 或 fifth root。
• Rollups：$F$的输入为：state Merkle root，以及，某些交易（non-deterministically），执行交易，输出：updated Merkle root。
• Turing-complete SNARK语言（如Lurk）的后端：$F$为执行a “step” of the program。

Nova的关键特性为：

• 无需trusted setup
• 所采用的vector commitment方案必须具有加法同态属性
• 仅针对R1CS instance，Fold scheme会将2个R1CS instance合并为1个R1CS instance。这些R1CS instance 必须具有完全相同的电路，即具有完全相同的$(A,B,C)$矩阵。
• 无需（如，通过FFT运算）做多项式除法和多项式乘法运算，可使用DLOG为hard的任意cycles of elliptic curves：
  • 可基于任意cycles of curves，如secp/secq。【详情见Spartan-ECDSA：最快的浏览器内 ZK secp256k1 ECDSA中的“附录：Secp256k1/Secq256k1曲线cycle”。】
  • 也可基于任意FFT-friendly cycles of curves，如Pasta（Pallas/Vesta）。【详情见：Halo2学习笔记——背景资料之Elliptic curves（5） 和 Mina中的Pasta（Pallas和Vesta）曲线。】
• $F$运算指定为R1CS表示
• 为理论上最简单的证明系统，同时提供了state-of-the-art efficiency：
  • Prover time：由2个size为$O(C)$的multiexps主导，其中，$C=|F|$
    • Nova的证明速度要比Groth16/PLONK/Halo等快5~50倍。
  • 具有Constant-sized verifier circuit（主要由2个scalar multiplication运算主导）：Nova的verifier circuit具有约2万个R1CS约束，是当前文献上记录的最小verifier circuit，意味着具有lowest recursion threshold。Nova的recursion开销比Halo的低7倍+，比Bunz等人2020年论文《Proof-carrying data without succinct arguments》方案低2倍+。
    
  • 压缩proof size为：$O(\log C)$个group elements：实际上只有数KB。

现有IVC方案对比：

为证明$y=F^{(n)}(x)$：

• 1）直观方法为：

  • 将$F$的$n$个迭代展开为一个电路

  • 对该单一电路应用某state-of-the-art SNARK来生成证明

    直观方法的缺陷为：

    • Prover所需内存为：$\Omega (n\ast |F|)$
    • proof 不是 incrementally updatable
    • 取决于具体的SNARK方案，Verifier time可能会依赖具体的$n$值（即，迭代次数）
• 2）Incrementally verifiable computation（IVC）[Val08, BCTV14]
  

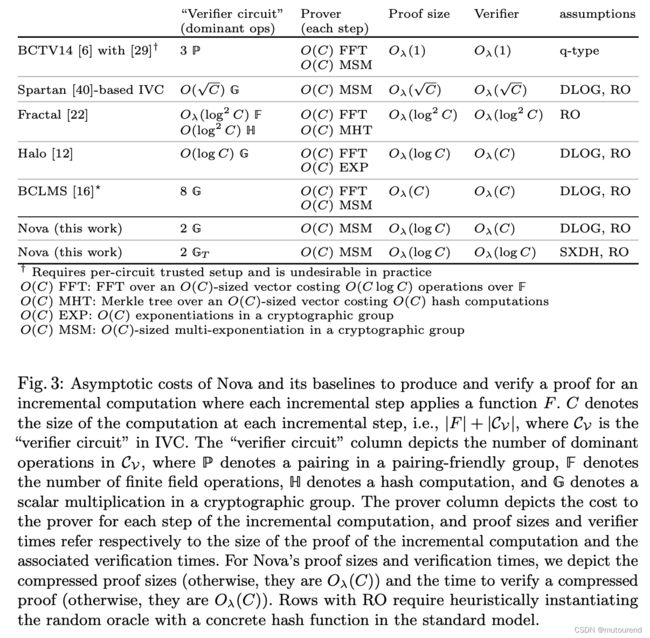
[Val08, BCTV14] IVC方案 与 Nova对比为：【其中[Set19]对应Spartan论文】

Nova 与 Bunz等人2021年论文BCLMS21 Proof-Carrying Data without Succinct Arguments中的“split accumulation”相关：

• Nova效率更高、更直接，且提供了a “native” scheme for proof compression。

Nova的秘密武器在于：Folding Schemes for NP：【下图的NP instance均为R1CS instance】

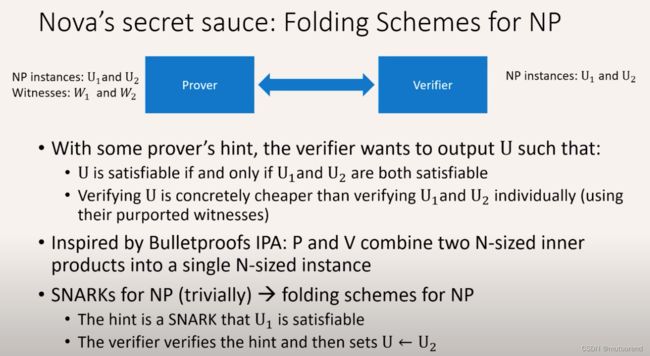
Nova的关键贡献在于：

• 不使用SNARKs 所实现的folding scheme for NP

R1CS回顾：

为实现R1CS的folding scheme，最直观但却错误的方式为：

即以上方案，对于$Z=(W,x,1)$，找不到相应的$r$，使得$AZ\circ BZ=CZ$，原因在于：

Nova的创新之一在于其所实现的Relaxed R1CS：【当$u=1,E=0$时，标准R1CS实例 为 Relaxed R1CS实例 的特例情况。】

针对Relaxed R1CS的folding scheme为：【即通过引入public input $u$和witness $E$来实现消减，以保证folding后仍能满足相同的relation关系】

根据relaxed R1CS的folding scheme所实现的IVC直观方案为：

不过，以上naive方案，IVC proof size为：$O(|F^{\prime }|)$个group elements。且存在以下2个问题：

• Proofs are large, both asymptotically and concretely
• Proofs are not zero-knowledge

原则上：借助zkSNARKs，$P$可证明the knowledge of a valid IVC proof，从而提供了succinctness和zero-knowledge。但是，借助zkSNARKs的方案是expensive的：

• $P$必须证明，如，其知道$W$对应承诺值$\hat{W}$，以及其他信息

为此，Nova创新之二是进行了proof压缩：

• 将对vectors的承诺值，解析为，对multilinear多项式的多项式承诺值
• 使用Spartan的变种，来直接证明承诺值$\hat{W}$满足相应的relaxed R1CS。
• 压缩后的proof size，由$O(|F^{\prime }|)$个group elements，降低为$O(\log |F^{\prime }|)$个group elements

也可以使用IPA（Inner Product Argument）来证明承诺值$\hat{W}$满足相应的relaxed R1CS:

• proof size可降低约5倍（可避免Spartan中的sum-check protocol，但在生成final proof时，会引入稍微高一点的开销）

Navo的缺陷有：

• zero-knowledge被限制在单个prover的context（zero-knowledge属性不是必须的）

当前的情况为：

• IVC proof size为：$O(|F^{\prime }|)$个group elements。
• 压缩的proof size为：$O(\log |F^{\prime }|)$个group elements，但是其不可incremental。

因此，一个open question为：

• 保持Nova其它特性的同时，能否构建具有succinct proof的IVC方案？
  Nova的一些优秀特性有：
  • smallest verifier circuit
  • efficient prover等等

当前的一些进展以及规划为：

---

最终的committed relaxed R1CS的folding scheme为：

借助Fiat-Shamir transform，将上述interactive folding scheme转换为non-interactive folding scheme：

所谓Nova，是指：

• 根据non-interactive folding scheme设计的IVC（Incrementally Verifiable Computation）方案。
• 借助具有简洁承诺值的任意加法同态承诺方案（如Pedersen commitment）来实例化。
• 额外使用某高效zkSNARK变种（如Spartan的变种）来证明knowledge of valid IVC proof，这样就具备了简洁性和零知识性，可提供简洁的、零知识的knowledge of valid IVC proof。
  • 注意Nova是不具备零知识属性的IVC方案。 因为对于零知识IVC方案，其要求IVC proof具备零知识属性。但是Nova中的IVC proof并不会隐藏与incremental computation steps相关的witnesses信息。
    对于单个Prover的情况下，这种差异问题不大，因为可借助Nova中的辅助zkSNARK来提供zero-knowledge proof of knowledge of a valid IVC proof。

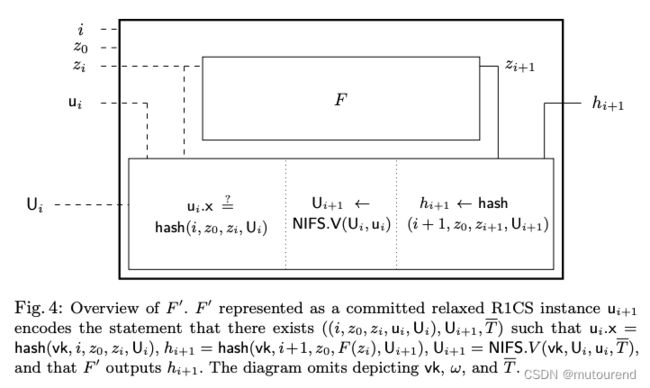
假设需构建一个基于folding scheme的IVC方案，其Prover需证明$z_n=F^n(z_0)$，基于初始输入$z_0$，重复执行某函数$F$ $n$次之后，输出结果为$z_n$。与SNARK-based IVC类似，基于folding scheme的IVC方案中，Prover使用扩展函数$F^{\prime }$，其包括：

• 调用函数$F$
• 记录之前对$F^{\prime }$函数调用的fold proofs

$F^{\prime }$的输入有：

• 2个committed relaxed R1CS instance $u_i$和$U_i$
  • $U_i$表示调用$F^{\prime }$ 第$1,\cdots ,i-1$次的正确执行
  • $u_i$表示调用$F^{\prime }$ 第$i$次的正确执行

$F^{\prime }$主要执行2个任务：

• 1）执行递归计算中的一步（一个step）：
  $F^{\prime }$可使用instance $u_i$中所包含的$z_i$来输出$z_{i+1}=F(z_i)$

• 2）$F^{\prime }$调用non-interactive folding scheme的Verifier，将：

  • checking $u_i$ task
  • 和 checking $U_i$ task

  fold为对单个instance $U_{i+1}$的checking task。

然后，IVC Prover会计算新的instance $u_{i+1}$，用于证明对$F^{\prime }$第$i+1$次调用执行的正确性，即IVC Prover会计算新的instance $u_{i+1}$来证明$z_{i+1}=F(z_i)$。
至此，有：

• $U_{i+1}$：表示调用$F^{\prime }$ 第$1,\cdots ,i-1,i$ 次的正确执行
• $u_{i+1}$：调用$F^{\prime }$ 第$i+1$次的正确执行

以上描述掩盖了一个细微的差异：

• 因为$F^{\prime }$必须输出running instance $U_{i+1}$供下次调用使用，$U_{i+1}$包含在$u_{i+1}.x$（即为$u_{i+1}$的public IO公共输入输出）中。
• 但是在下一次迭代时，$F^{\prime }$必须将$u_{i+1}.x$ fold into $U_{i+1}.x$，即意味着$F^{\prime }$将陷入squeeze $U_{i+1}$ into $U_{i+1}.x$的困境。

为解决这种不一致性，$F^{\prime }$不再直接输出$U_{i+1}$，而是修改$F^{\prime }$的输出为其public IO的抗碰撞哈希值，这样可确保$F^{\prime }$的public IO为常量个有限域元素。下一次调用$F^{\prime }$时，额外将该哈希值的preimage作为non-deterministic advice。可假设该哈希函数还会额外输入一个随机值以提供hiding属性，不过为便于表示这里不明确描述。

以不存在witness的标准R1CS特例情况为例：【即$E为0向量，W为0向量，x为0向量，u为0$】
令$(u_{\perp },w_{\perp })$为trivially satisfying instance-witness pair，其中$E,W,x$为appropriately-sized zero vectors，$r_E=0,r_W=0$，$\bar{E}和\bar{W}$分别为$E,W$的承诺值。
在第$i+1$次迭代时，IVC Prover运行$F^{\prime }$，计算$u_{i+1}和U_{i+1}$的同时，还会计算$w_{i+1}和W_{i+1}$.。由于$u_{i+1}和U_{i+1}$证明了对$F^{\prime }$的$i+1$次调用的正确性（进而间接证明了对$F$的$i+1$次调用的正确性），相应的IVC proof为$(U_{i+1},W_{i+1}),(u_{i+1},w_{i+1})$。其简洁性由底层的folding scheme提供。
具体的IVC构建为：

因为$F^{\prime }$可 以polynomial time计算，可将$F^{\prime }$表示为一个committed relaxed R1CS structure $s_{F^{\prime }}$。令：
$(u_{i+1},w_{i+1})\leftarrow \text{trace}(F^{\prime },(vk,U_i,u_i,(i,z_0,z_i),w_i,\bar{T}))$
表示基于non-deterministic advice $(vk,U_i,u_i,(i,z_0,z_i),w_i,\bar{T})$运行$F^{\prime }$的satisfying committed relaxed R1CS instance-witness pair $(u_{i+1},w_{i+1})$。

具体的IVC方案$(\mathcal{G},\mathcal{K},\mathcal{P},\mathcal{V})$定义如下：

以上IVC方案$(\mathcal{G},\mathcal{K},\mathcal{P},\mathcal{V})$的efficiency为：

不过，以上IVC proof：

• 不具有零知识性：因以上IVC proof没有隐藏Prover的non-deterministic inputs。
• 不具有简洁性：因以上IVC proof size与$F$ size呈线性关系。

接下来，是使用zkSNARKs来压缩IVC proof：

• 用于证明其知道${\Pi }_i$，使得IVC Verifier $\mathcal{V}$ accepts for statement $(i,z_0,z_i)$。
• 借助zkSNARKs生成的proof，具有与zkSNARKs对应的简洁性和零知识性。

使用zkSNARKs来证明the knowledge of a valid IVC proof的基本原理为：

2. 使用Spartan变种来压缩Nova IVC proof

不过在实例化时，需要针对committed relaxed R1CS的zkSNARK方案，来证明the knowledge of a valid IVC proof succinctly and in zero-knowledge。

Spartan具有无需FFT运算和trusted setup的特性，在Nova论文中，采用了Spartan的改写版zkSNARK方案来实现IVC proof压缩。

2.1 Spartan背景知识

• polynomial extension定义：每个函数$f:\{0,1{\}}^l\to \mathbb{F}$具有唯一的MLE，反之，每个基于$\mathbb{F}$的$l$-变量multilinear多项式 唯一 extends 某个唯一函数mapping $\{0,1{\}}^l\to \mathbb{F}$。本文以$\tilde{f}$来表示$f$的唯一MLE。
  
• sum-check protocol协议：
  

2.2 针对Idealized Relaxed R1CS的polynomial IOP

Nova论文中基于Spartan，将Spartan的 polynomial IOP for R1CS 逐字改编为 polynomial IOP for relaxed R1CS：





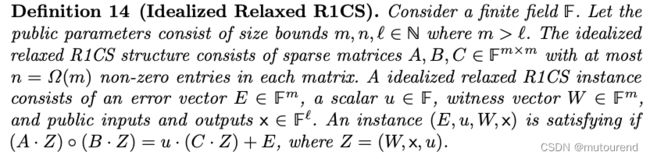
针对Idealized Relaxed R1CS的polynomial IOP具体为：

注意：

• 对上面的Equation（2）应用sum-check protocol的soundness error至多为$O(\log m)/|\mathbb{F}|$。
• 共使用了4次sum-check protocol，其中有3次可并行调用，且可合并为一个sum-check protocol。每次调用sum-check protocol时，相应的多项式在每个变量的degree最多为3，且变量数为$s=\log m$，因此该polynomial IOP的round复杂度为$O(\log m)$。由于每个多项式的每个变量degree至多为3，总的communication cost为$O(\log m)$个field elements。
• Verifier runtime与sum-check protocol Verifier runtime一致。$\widetilde{eq}$ evaluate at任意input $(\tau ,r_x)\in {\mathbb{F}}^{2s}$仅需$O(\log m)$次filed运算。
• 与Spartan的Prover在polynomial IOP的工作量一致，采用Libra等之前的技术，仅需要$O(n)$次基于$\mathbb{F}$的运算。

2.3 将Polynomial IOPs编译为zkSNARKs

与SuperSonic、Marlin、Spartan中类似，借助多项式承诺方案和Fiat-Shamir transform来将Polynomial IOPs编译为zkSNARKs。

关键点有：

• 1）将向量承诺解析为multilinear多项式承诺：
  可将$m$-sized 向量 看成是 $\log m$-变量multilinear多项式在$\{0,1{\}}^{\log m}$的evaluation值集合。现有的针对 $\log m$-变量multilinear多项式 承诺方案有：【二者主要差别在于Verifier time】

  • 1.1）$P{C}_{BP}$：采用Pedersen多项式承诺方案来对向量进行承诺，与Hyrax中类似，Bulletproofs可提供合适的inner product证明协议。基于的安全假设为DLOG。对于$\log m$-变量multilinear多项式，承诺用时$O_{\lambda }(m)$，生成的承诺值长度为$O_{\lambda }(1)$。Prover开销为$O_{\lambda }(m)$，proof size为$O_{\lambda }(\log m)$，Verifier验证用时为$O_{\lambda }(m)$。注意$P{C}_{BP}$为Hyrax多项式承诺的特例情况。
    
  • 1.2）$P{C}_{Dory}$：将向量承诺看成是对2层矩阵承诺值的承诺，详细见[19, 34]论文中的例子。基于SXDH安全假设。Dory [34]提供了所需的inner product argument。承诺用时$O_{\lambda }(m)$，生成的承诺值长度为$O_{\lambda }(1)$。Prover开销为$O_{\lambda }(m)$，proof size为$O_{\lambda }(\log m)$，Verifier验证用时为$O_{\lambda }(\log m)$。

• 2）针对sparse multilinear多项式的多项式承诺方案：不过，本文实际需要的是可高效处理sparse multilinear多项式的多项式承诺方案。Spartan论文中第7章和Quarks论文第6章中，提供了将现有 “multilinear多项式的多项式承诺方案” 编译为 “sparse multilinear多项式的多项式承诺方案” 的通用编译器。从而可将$P{C}_{BP}$和$P{C}_{Dory}$分别编译为“Sparse-$P{C}_{BP}$”和“Sparse-$P{C}_{Dory}$”。从而分别有：

  • 基于“Sparse-$P{C}_{BP}$”的zkSNARK：
    

  • 基于“Sparse-$P{C}_{Dory}$”的zkSNARK：