机器学习真的能预测股价吗?
刚接触各种统计模型和机器学习模型的时候,肯定很多人都抱着类似的幻想:将搜集来的各种数据丢到模型中构建一个预测股价的模型,希望每天打开电脑跑一遍模型,预测下一个交易日的价格,以此决定今天如何交易。
抱有类似幻想小伙伴也一定在网上搜过机器学习预测股价的一系列教程,我在youtube上就看到过一个7万粉丝的大V用LSTM预测股价。初入机器学习的小伙伴在看完教程之后,发现原来预测股价竟然这样容易,仿佛找到了投资的圣杯,财富自由指日可待。
下图就是用LSTM做的股价预测模型,无论训练集、验证集还有测试集都与实际行情“完美重合”。
然而,预测美如画,实盘亏成狗。本期就从时间序列分析模型ARIMA和深度学习模型LSTM两个例子讲讲,如此的比例建模逻辑错在哪,应该怎样做,股价到底能不能预测?
ps:之所以选择ARIMA和LSTM,是因为这两个模型是被各种“大V”用的最多的预测股价的模型。
一、ARIMA(Autoregressive Integrated Moving Average Model)
ARIMA常用于时间序列分析,是AR、MA和差分的结合,本质就是线性回归模型。ARIMA有三个参数,表示为ARIMA(p, d, q):
- p:自回归(AR)模型的阶数,即滞后项的数量,通过PACF图确定。
- d:差分的阶数。经过d阶差分后,原时间序列数据应当平稳,d最好不要超过2。
- q:移动平均(MA)模型的阶数,通过ACF图确定。
另外介绍几个重要特例:
- ARIMA(p, 0, 0)就是AR§ 或 ARMA(p, 0)
- ARIMA(p, 0, 0)就是MA(q) 或 ARMA(0, q)
- ARIMA(0, d, 0)就是I(d)
- ARIMA(0, 1, 0)就是I(1),即随机游走(random walk)
关于ARIMA的更多内容可以参见之前的文章《时间序列分析基础(二)》。
本期用pmdarima库自动化实现ARIMA的调参与建模,看一下ARIMA预测股价的效果如何。模型构建要素:
- 数据:BTC 和 EOS 的1小时收盘价格
- 回测区间:2019-01-01至2020-12-31
- 模型:ARIMA
- 训练集比例:80%
下面开始训练模型(这里不考虑季节性因素对价格的影响)
import pmdarima as pm # Pmdarima是一个统计学的库,用于时间序列分析,其中一个重要功能就是可以自动化构建最优的arima模型
model = pm.auto_arima(train,
error_action='ignore', trace=False,
suppress_warnings=True, maxiter=10,
seasonal=False)
上图展现了在训练集和测试集整体效果,训练集几乎完美拟合了价格走势,但测试集的预测值几乎是一条直线。红色阴影部分代表预测的置信区间,也就是说模型认为价格走势有更高的概率在阴影范围内波动。就预测精确度上,模型没表现出什么预测能力,但EOS价格走势整体还是在置信区间中。 再来看看BTC的预测效果: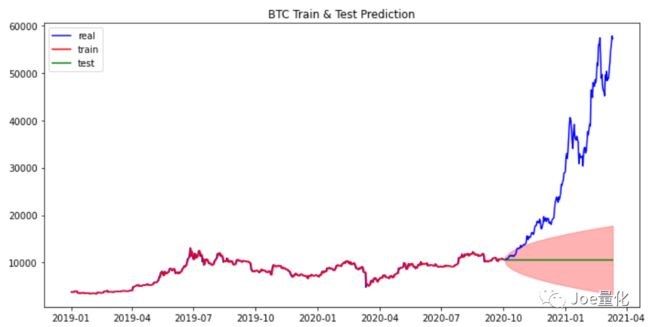
从BTC的预测结果来看可以用灾难来形容,完美错过了去年开始的行情。有人可能会说,ARIMA模型不行,应该用牛逼的深度学习。好,那我们来看看LSTM。
二、LSTM(Long short-term memory)
LSTM是特殊的循环神经网络(RNN),适合用在序列数据上,例如自然语言处理、股票数据等。RNN有短期记忆问题,无法处理很长的输入序列训练。因为随着长序列训练过程的推进,会出现梯度消失的问题。梯度是用来更新神经网络权重的。如果梯度过小,那么每次更新的权重对下一次训练的影响将非常的小,这时模型将停止学习或学习的十分缓慢。而LSTM 通过巧妙的设计可以记住长期的信息且无需付出很大代价。
上面看不懂没关系,这不是本期的重点,只要记住LSTM很牛逼,能够用来对时间序列数据建模就够了。 接下来,我们来复刻youtube上的代码,用LSTM预测BTC的价格。与之前一样,我们用2019-01-01至2020-12-31BTC 1小时收盘价格数据,将数据按照8:2 拆分成训练集和测试集。另外,取2021-01-01至2021-03-12之间的数据作为样本外验证(该部分数据在模型训练过程中是看不到的,用来检验模型的效果)。在正式训练模型之前,还要说明一下特征与标签如何分配。假设用过去4小时的收盘价预测下一个小时的收盘价。我们用滚动的方式训练,第一行相当于第一个样本,取过去4小时的收盘价数据作为特征(y1到y4),y5作为标签。第二行作为第二个样本,取y2到y5作为特征,y6作为标签,以此类推。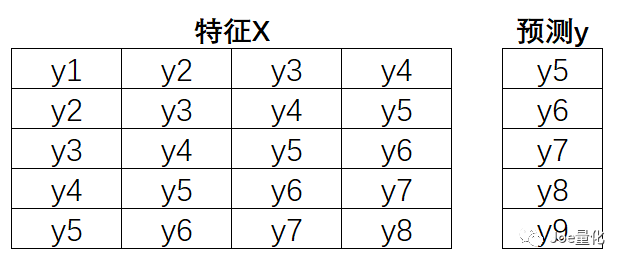
下面上代码。
from sklearn.preprocessing import MinMaxScaler
from keras.models import Sequential
from keras.layers import Dense, LSTM
# 去纲量
scaler = MinMaxScaler()
data_scaler = scaler.fit_transform(data[['close']])
# 拆分训练集和测试集
Ntrain = int(0.8* data_scaler.shape[0])
train = data_scaler[:Ntrain]
# 滚动构建特征和标签
x_train = []
y_train =[]
fori in range(60, len(train)):
x_train.append(train[i-60:i, 0])
y_train.append(train[i, 0])
# 转换成keras要求的shape
x_train, y_train= np.array(x_train), np.array(y_train)
x_train = np.reshape(x_train, (x_train.shape[0], x_train.shape[1], 1)) # 最后一个为特征数量,因为只有一个特征close
# 建立模型
model = Sequential()
model.add(LSTM(50, return_sequences=True, input_shape=(x_train.shape[1], 1))) # 50个神经元
model.add(LSTM(50, return_sequences=False))
model.add(Dense(25))
model.add(Dense(1))
# 均方误差作为评价指标
model.compile(optimizer='adam', loss='mean_squared_error')
model.fit(x_train, y_train, batch_size=1, epochs=1)
经过以上过程,我们就得到了类似文章开头的美如画的预测。无论是验证集还是测试集(样本外),LSTM几乎都实现了完美的预测。事实真的是这样吗?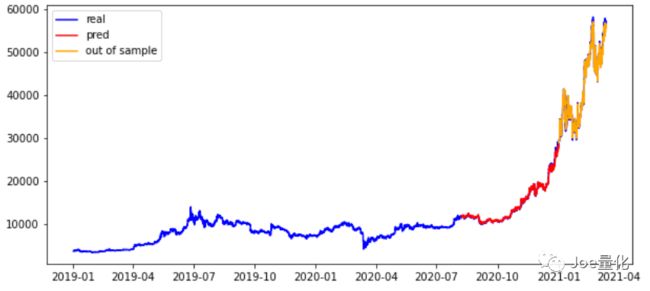
由于数据比较密集,肉眼不容易辨别,我们来看下不同数据集的均方误差表现。除了对比测试集与样本外数据以外,还加入了naive forecast预测结果的对比。在预测价格的背景下,naive forecast就是指价格符合随机游走,最好的预测就是本期价格就是下一周期的价格。(如果预测上涨还是下跌,naive forecast就是指50%的概率上涨,50%的概率下跌) 
由上图结果看出,**样本外数据的均方误差相比测试集翻了一倍,而且接近naive forecast。说明样本外预测的效果没比瞎猜好多少。**接下来,我们再截取一小段时间,看看模型的预测效果。下图能够看出,虽然预测值与真实值非常相似,但是预测值滞后了1个周期,也就是说该模型只不过是单纯的用当期收盘价作为下一期的收盘价,跟naive forecast没什么区别。
三、如何正确构建模型
看到这里,有人会问,难道机器学习没用?不是机器学习没用,是建模方式错了。首先,我们需要搞清楚机器学习的3个重要特点:
- 一个重要的假设:历史数据和未来数据都服从相同的分布。比如用环卫工人的历史工资数据训练出来的模型,无法预测程序员的工资,因为二者的分布是不同的。
- 机器学习是用来识别模式的(pattern recognition)。如果模式变了,模型当然失效。这也是为什么机器学习在高频交易领域更有效,因为模式在短期内更有可能保持不变;
- **机器学习不宜用做外推法,涨跌幅比价格更适合作为标签。**比如,茅台股价在之前长期处于500元以下,模型会自动将未来预测的股价限定在500以内,但是我们都知道茅台股价已经超过了2000。而涨跌幅会有一个波动的范围,使得模型更容易识别。
接下来,纠正2个错误观念:
- **天上没有掉馅饼的好事,不要尝试去预测股价,不要尝试去预测股价,不要尝试去预测股价。**很多人亏钱就是老想着预测市场怎么走,而不是用统计性思维去理解市场。其实搭配合理的资金管理策略,即使用抛硬币的方式决定交易信号也是可以大概率赚钱的。如果把把梭哈,即使你有90%的胜率也会早晚亏个精光。
- 不要迷信机器学习。机器学习更像是一个实验,而不是圣经。
最后,说一下正确的做法:
- 用涨跌幅或收益率作为预测的目标;
- 用ARIMA做时间序列分析而不是预测,加深对数据的理解更重要;
- 数据集分成三份,留一份用于样本外检验;(更多内容见《金融时间序列Cross-Validation你用对了吗?(附代码)》)
- 对比naive forecast,检验模型是否真的有效。




