Codeforces Round #792 (Div. 1 + Div. 2)
比赛链接：Dashboard - Codeforces Round #792 (Div. 1 + Div. 2) - Codeforces
A: 思维
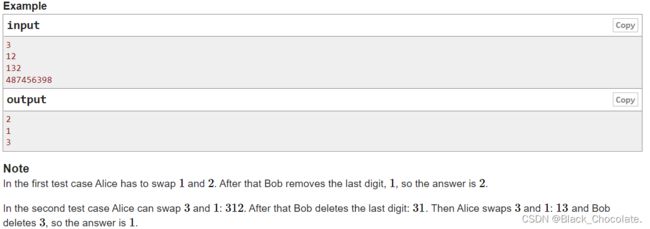题意：Alice和Bob在玩游戏，每次等Alice交换两个不同位置的数后，Bob就会删除最后一个位置上的数，当最终只剩下一个数后，游戏结束。保证使这个数最小，问最小是多少？
分析：
特判一下。如果数的长度为2，那么Alice必须交换一次，Bob才能删除。所以ans就是第二个数。
一般情况：无论怎么操作，Alice是一定可以把最小值放在最前面。
代码：
#include
#define all(v) v.begin(),v.end()
#define int long long
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define pi acos(-1)
using namespace std;
const int INF=0x3f3f3f3f;
const int N=2e7+10;
typedef pairPII;
inline void solve(){
string s;cin>>s;
if(s.size()==2){
cout<>T;
while(T--) solve();
} B:构造
题意：给定三个数a，b，c。使其满足题中的三个条件的x，y，z。任意输出x，y，z
分析：前置芝士：a
所以我们可以显然构造出：x=a+b+c，y=b+c，z=c。
代码：
#include
#define all(v) v.begin(),v.end()
#define int long long
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define pi acos(-1)
using namespace std;
const int INF=0x3f3f3f3f;
const int N=2e7+10;
typedef pairPII;
inline void solve(){
int a,b,c;cin>>a>>b>>c;
cout<>T;
while(T--) solve();
} C:模拟+排序
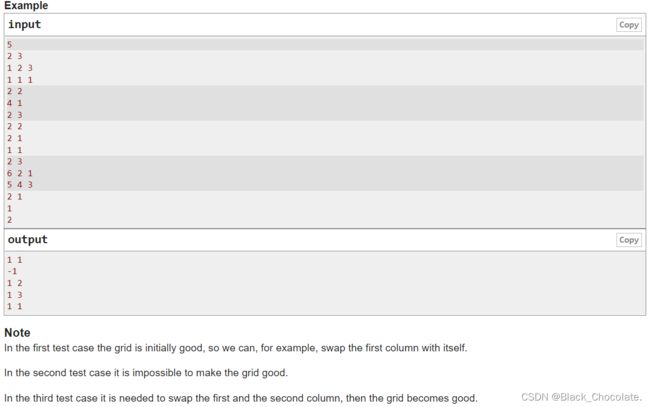题意：给定一个矩阵，问是否只交换矩阵中的两列（可以是相同的两列），使得矩阵中每行的元素都是非降的。
思路：我们先给每一行进行排序，然后我们将改变后的矩阵跟原矩阵进行对比。找出错位的位置，然后把这两列交换，如果交换后满足条件，就输出这两列，否则就输出-1.
ps:如果错位的个数多于两个，那么不管交换哪两列，都不会满足条件（具体看代码）
代码：
#include
#define all(v) v.begin(),v.end()
#define int long long
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define pi acos(-1)
using namespace std;
const int INF=0x3f3f3f3f;
const int N=2e7+10;
typedef pairPII;
int n,m;
//用于交换矩阵中的两列
inline void Swap(int x,int y,vector>&a){
for(int i=0;i>n>>m;
vector>a(n,vector(m));/*这里做解释一下：这里相当于重新定义了一下二维数组：表示：vector类型的a数组，数组每个值是vector类型，大小是：a(n,vector(m))是指有n行，每行有m个元素*/
for(int i=0;i>a[i][j];
}
}
vector>b=a;//用矩阵b复制矩阵a
setse;
bool ok=false;
for(int i=0;ipos;//用vector接受set容器中的值
for(auto i:se) pos.push_back(i);
Swap(pos[0],pos[1],a);//交换列
for(int i=0;i>T;
while(T--) solve();
} D：贪心
题意：有 n 个陷阱，每个陷阱造成 ai 点伤害，最多跳过 k 个陷阱，但如果选择跳过这个陷阱的话，后面的每个陷阱的伤害都会加 1，问最少伤害是多少
吐槽：这题相通了很简单，想不通就一愣一愣的。
这里参考的是ygg的题解：
Codeforces Round #792 (Div. 1 + Div. 2) D(贪心) E(贪心) - 知乎
分析：先考虑。最优的方案肯定是把给定的次数给跳完。问题就在于，每跳一个，跳过的位置后面的伤害就会+1。如何跳？
错误方法：直接从后往前面选择k个陷阱跳完——然后就g啦！
正确方法： 假设我们跳过的第一个陷阱为i，那么对答案的贡献就是a[i]（这里的贡献是指，总和减去a[i]）。但是后面的伤害都会+1，所以对于单个陷阱i而言，它对答案的贡献为 a[i]+(n-i)。
a[i]+(n-i)：跳过点i后会对答案贡献原始的a[i]伤害+（跳完后）后面的（n-i）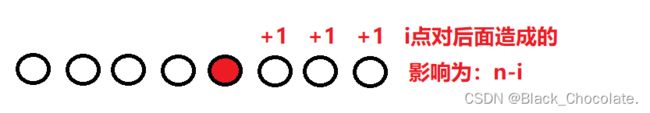
跳完第一个陷阱，后面还有k-1个跳过陷阱的机会，所以该点对答案的贡献同理：伤害减少k-1。
k-2：伤害减少k-2。然后我们就可以推出仅跟k相关的减少伤害量： 
根据前面的推理：每个位置对于伤害的贡献为 -a[i]+(n-i)=n-(a[i]+i)
令v[i]=n-(a[i]+i)，然后选择k最小的k个即可。具体看代码：
代码：
#include
#define all(v) v.begin(),v.end()
#define int long long
#define fast ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
#define pi acos(-1)
using namespace std;
const int INF=0x3f3f3f3f;
const int N=2e7+10;
typedef pairPII;
int a[N];
inline void solve(){
int n,k;cin>>n>>k;
for(int i=1;i<=n;i++) cin>>a[i];
vectorve;
for(int i=1;i<=n;i++) ve.push_back(n-(a[i]+i));//放入每个点对答案的贡献
int ans=accumulate(a+1,a+1+n,0LL);//原始累加和
sort(all(ve));//将贡献进行排序
for(int i=0;i>T;
while(T--) solve();
}