C语言督学营 高级笔记 (Day1~2)

一研为定

高级第一次 直播 归并排序

关于数组下标越界的解决办法：

if(j==-1){
    break ;   // 在边界进行判断
}

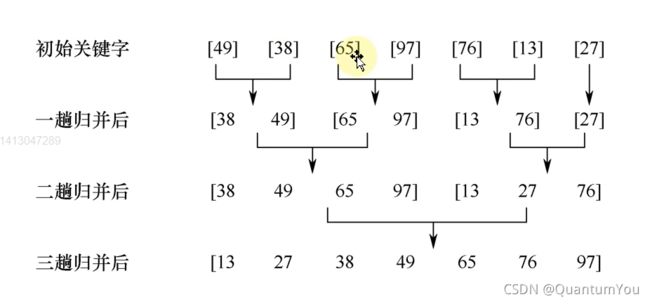
归并排序

归并排序代码

#include 
#include 

#define N 7
typedef int ElemType;
//49,38,65,97,76,13,27
void Merge(ElemType A[],int low,int mid,int high)
{
	ElemType B[N];//为了降低操作次数
	int i,j,k;
	for(k=low;k<=high;k++)//复制元素到B中
		B[k]=A[k];
	for(i=low,j=mid+1,k=i;i<=mid&&j<=high;k++)//合并两个有序数组
	{
		if(B[i]<=B[j])
			A[k]=B[i++];
		else
			A[k]=B[j++];
	}
	while(i<=mid)//如果有剩余元素，接着放入即可
		A[k++]=B[i++];
	while(j<=high)
		A[k++]=B[j++];
}
//归并排序不限制是两两归并，还是多个归并
// 1 3 5 7 9
// 2 4
// 1 2 3 4 5 7 9  主要的代码逻辑
void MergeSort(ElemType A[],int low,int high)//递归分割
{
	if(low<high)
	{
		int mid=(low+high)/2;
		MergeSort(A,low,mid);
		MergeSort(A,mid+1,high);
		Merge(A,low,mid,high);
	}
}
void print(int* a)
{
	for(int i=0;i<N;i++)
	{
		printf("%3d",a[i]);
	}
	printf("\n");
}

// 归并排序
int main()
{
	int A[7]={49,38,65,97,76,13,27};//数组，7个元素
	MergeSort(A,0,6);
	print(A);
	system("pause");
}

各大算法时间复杂度

• 快排算法：最坏情况，时间复杂度为 O（n^2）,即为数组本身有序的情况，解决办法使用随机数

基数排序

计数排序

高级第二次 直播 图

图

• 图G由顶点集 V 和边集 E 组成，记为G=(V,E)其中V( G )表示图G中顶点的有限非空集：E( G )表示图G中顶点之间的关系（边）集合

图的存储方法

• 邻接矩阵，邻接表

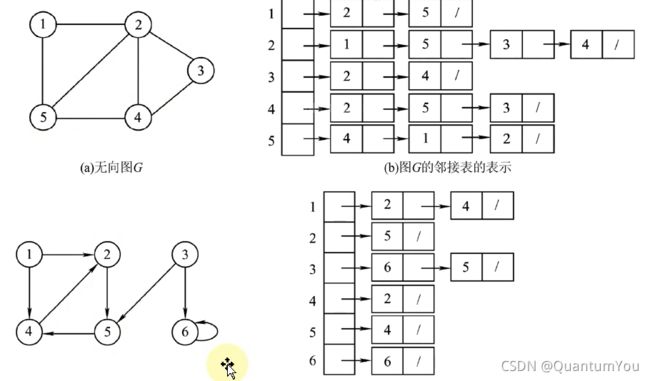
• 邻接表的定义

• 当一个图为稀疏图时，使用邻接矩阵法显然要浪费大量的存储空间，而图的邻接表法结合了顺序存储和链式存储方法，大大减少了这种不必要的浪费所谓邻接表，是指对图G中的每个顶点v建立一个单链表。

邻接表的定义

图的存储代码

#include 
#include 
#include 
#include 

#define MAX 100
#define isLetter(a)  ((((a)>='a')&&((a)<='z')) || (((a)>='A')&&((a)<='Z')))
#define LENGTH(a)  (sizeof(a)/sizeof(a[0]))

// 邻接表中表对应的链表的顶点
typedef struct _ENode
{
    int ivex;                   // 该边所指向的顶点的位置,是数组的下标
    struct _ENode *next_edge;   // 指向下一条弧的指针
}ENode, *PENode;

// 邻接表中表的顶点
typedef struct _VNode
{
    char data;              // 顶点信息
    ENode *first_edge;      // 指向第一条依附该顶点的弧
}VNode;

// 邻接表
typedef struct _LGraph
{
    int vexnum;             // 图的顶点的数目
    int edgnum;             // 图的边的数目
    VNode vexs[MAX];
}LGraph;

/*
 * 返回ch在matrix矩阵中的位置
 */
static int get_position(LGraph g, char ch)
{
    int i;
    for(i=0; i<g.vexnum; i++)//去顶点结构体数组中遍历每个顶点
        if(g.vexs[i].data==ch)
            return i;//返回的是对应顶点的下标
    return -1;
}

/*
 * 读取一个输入字符
 */
static char read_char()
{
    char ch;

    do {
        ch = getchar();
    } while(!isLetter(ch));

    return ch;
}

/*
 * 将node链接到list的末尾
 */
static void link_last(ENode *list, ENode *node)
{
    ENode *p = list;

    while(p->next_edge)
        p = p->next_edge;
    p->next_edge = node;
}

/*
 * 创建邻接表对应的图(自己输入)
 */
LGraph* create_lgraph()
{
    char c1, c2;
    int v, e;
    int i, p1, p2;
    ENode *node1, *node2;
    LGraph* pG;

    // 输入"顶点数"和"边数"
    printf("input vertex number: ");
    scanf("%d", &v);
    printf("input edge number: ");
    scanf("%d", &e);
    if ( v < 1 || e < 1 || (e > (v * (v-1))))
    {
        printf("input error: invalid parameters!\n");
        return NULL;
    }
 
    if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )
        return NULL;
    memset(pG, 0, sizeof(LGraph));

    // 初始化"顶点数"和"边数"
    pG->vexnum = v;
    pG->edgnum = e;
    // 初始化"邻接表"的顶点
    for(i=0; i<pG->vexnum; i++)
    {
        printf("vertex(%d): ", i);
        pG->vexs[i].data = read_char();
        pG->vexs[i].first_edge = NULL;
    }

    // 初始化"邻接表"的边
    for(i=0; i<pG->edgnum; i++)
    {
        // 读取边的起始顶点和结束顶点
        printf("edge(%d): ", i);
        c1 = read_char();
        c2 = read_char();

        p1 = get_position(*pG, c1);
        p2 = get_position(*pG, c2);

        // 初始化node1
        node1 = (ENode*)calloc(1,sizeof(ENode));
        node1->ivex = p2;
        // 将node1链接到"p1所在链表的末尾"
        if(pG->vexs[p1].first_edge == NULL)
          pG->vexs[p1].first_edge = node1;
        else
            link_last(pG->vexs[p1].first_edge, node1);
        // 初始化node2
        node2 = (ENode*)calloc(1,sizeof(ENode));
        node2->ivex = p1;
        // 将node2链接到"p2所在链表的末尾"
        if(pG->vexs[p2].first_edge == NULL)
          pG->vexs[p2].first_edge = node2;
        else
            link_last(pG->vexs[p2].first_edge, node2);
    }

    return pG;
}

/*
 * 创建邻接表对应的图(用已提供的数据)，无向图
 */
LGraph* create_example_lgraph()
{
    char c1, c2;
    char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
    char edges[][2] = {
        {'A', 'C'}, 
        {'A', 'D'}, 
        {'A', 'F'}, 
        {'B', 'C'}, 
        {'C', 'D'}, 
        {'E', 'G'}, 
        {'F', 'G'}}; 
    int vlen = LENGTH(vexs);
    int elen = LENGTH(edges);
    //上面类似一个邻接矩阵存储
    int i, p1, p2;
    ENode *node1, *node2;
    LGraph* pG;//pG表示图


    if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )
        return NULL;
    memset(pG, 0, sizeof(LGraph));//就是把申请的空间内初始化为零

    // 初始化"顶点数"和"边数"
    pG->vexnum = vlen;
    pG->edgnum = elen;
    // 初始化"邻接表"的顶点
    for(i=0; i<pG->vexnum; i++)
    {
        pG->vexs[i].data = vexs[i];
        pG->vexs[i].first_edge = NULL;
    }

    // 初始化"邻接表"的边
    for(i=0; i<pG->edgnum; i++)
    {
        // 读取边的起始顶点和结束顶点
        c1 = edges[i][0];
        c2 = edges[i][1];

        p1 = get_position(*pG, c1);//p1对应起始顶点下标位置
        p2 = get_position(*pG, c2);//p1对应结束顶点下标位置

        // 初始化node1
        node1 = (ENode*)calloc(1,sizeof(ENode));
        node1->ivex = p2;
        // 将node1链接到"p1所在链表的末尾"
        if(pG->vexs[p1].first_edge == NULL)
            pG->vexs[p1].first_edge = node1;
        else
            link_last(pG->vexs[p1].first_edge, node1);
        // 初始化node2
        node2 = (ENode*)calloc(1,sizeof(ENode));
        node2->ivex = p1;
        // 将node2链接到"p2所在链表的末尾"
        if(pG->vexs[p2].first_edge == NULL)
            pG->vexs[p2].first_edge = node2;
        else
            link_last(pG->vexs[p2].first_edge, node2);
    }

    return pG;
}

/*
 * 深度优先搜索遍历图的递归实现
 */
static void DFS(LGraph G, int i, int *visited)
{
    ENode *node;

    visited[i] = 1;//要访问当前结点了，所以打印
    printf("%c ", G.vexs[i].data);
    node = G.vexs[i].first_edge;//拿当前顶点的后面一个顶点
    while (node != NULL)
    {
        if (!visited[node->ivex])//只要对应顶点没有访问过，深入到下一个顶点访问
            DFS(G, node->ivex, visited);
        node = node->next_edge;//某个顶点的下一条边，例如B结点的下一条边
    }
}

/*
 * 深度优先搜索遍历图
 */
void DFSTraverse(LGraph G)
{
    int i;
    int visited[MAX];       // 顶点访问标记

    // 初始化所有顶点都没有被访问
    for (i = 0; i < G.vexnum; i++)
        visited[i] = 0;

    printf("DFS: ");
	//从A开始深度优先遍历
    for (i = 0; i < G.vexnum; i++)
    {
        if (!visited[i])
            DFS(G, i, visited);
    }
    printf("\n");
}

/*
 * 广度优先搜索（类似于树的层次遍历）
 */
void BFS(LGraph G)
{
    int head = 0;
    int rear = 0;
    int queue[MAX];     // 辅组队列
    int visited[MAX];   // 顶点访问标记
    int i, j, k;
    ENode *node;

	//每个顶点未被访问
    for (i = 0; i < G.vexnum; i++)
        visited[i] = 0;
	//从零号顶点开始遍历
    printf("BFS: ");
    for (i = 0; i < G.vexnum; i++)//对每个连同分量均调用一次BFS
    {
        if (!visited[i])//如果没访问过，就打印，同时入队,最初是A
        {
            visited[i] = 1;//标记已经访问过
            printf("%c ", G.vexs[i].data);
            queue[rear++] = i;  // 入队列
        }
        while (head != rear) //第一个进来的是A，遍历A的每一条边
        {
            j = queue[head++];  // 出队列
            node = G.vexs[j].first_edge;
            while (node != NULL)
            {
                k = node->ivex;
                if (!visited[k])
                {
                    visited[k] = 1;
                    printf("%c ", G.vexs[k].data);
                    queue[rear++] = k;//类似于树的层次遍历，遍历到的同时入队
                }
                node = node->next_edge;
            }
        }
    }
    printf("\n");
}

/*
 * 打印邻接表图
 */
void print_lgraph(LGraph G)
{
    int i;
    ENode *node;

    printf("List Graph:\n");
    for (i = 0; i < G.vexnum; i++)//遍历所有的顶点
    {
        printf("%d(%c): ", i, G.vexs[i].data);
        node = G.vexs[i].first_edge;
        while (node != NULL)//把每个顶点周围的结点都输出一下
        {
            printf("%d(%c) ", node->ivex, G.vexs[node->ivex].data);
            node = node->next_edge;
        }
        printf("\n");
    }
}
/*
 * 创建邻接表对应的图(有向图)
 */
LGraph* create_example_lgraph_directed()
{
    char c1, c2;
    char vexs[] = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
    char edges[][2] = {
        {'A', 'B'}, 
        {'B', 'C'}, 
        {'B', 'E'}, 
        {'B', 'F'}, 
        {'C', 'E'}, 
        {'D', 'C'}, 
        {'E', 'B'}, 
        {'E', 'D'}, 
        {'F', 'G'}}; 
    int vlen = LENGTH(vexs);
    int elen = LENGTH(edges);
    int i, p1, p2;
    ENode *node1;
    LGraph* pG;


    if ((pG=(LGraph*)malloc(sizeof(LGraph))) == NULL )
        return NULL;
    memset(pG, 0, sizeof(LGraph));

    // 初始化"顶点数"和"边数"
    pG->vexnum = vlen;
    pG->edgnum = elen;
    // 初始化"邻接表"的顶点
    for(i=0; i<pG->vexnum; i++)
    {
        pG->vexs[i].data = vexs[i];
        pG->vexs[i].first_edge = NULL;
    }

    // 初始化"邻接表"的边
    for(i=0; i<pG->edgnum; i++)
    {
        // 读取边的起始顶点和结束顶点
        c1 = edges[i][0];
        c2 = edges[i][1];

        p1 = get_position(*pG, c1);
        p2 = get_position(*pG, c2);
        // 初始化node1
        node1 = (ENode*)calloc(1,sizeof(ENode));
        node1->ivex = p2;
        // 将node1链接到"p1所在链表的末尾"
        if(pG->vexs[p1].first_edge == NULL)
            pG->vexs[p1].first_edge = node1;
        else
            link_last(pG->vexs[p1].first_edge, node1);
    }

    return pG;
}
//图的创建，打印，广度优先遍历，深度优先遍历
//有向图
void main()
{
    LGraph* pG;

    // 无向图自定义"图"(自己输入数据，输入的方法可以参考create_example_lgraph初始化好的数据)
    //pG = create_lgraph();
     无向图的创建，采用已有的"图"
    //pG = create_example_lgraph();
	//有向图的创建
	pG = create_example_lgraph_directed();
    // 打印图
    print_lgraph(*pG);
    DFSTraverse(*pG);//深度优先遍历
	BFS(*pG);//广度优先遍历
	system("pause");
}