力扣每日一题2023.7.13

题目:

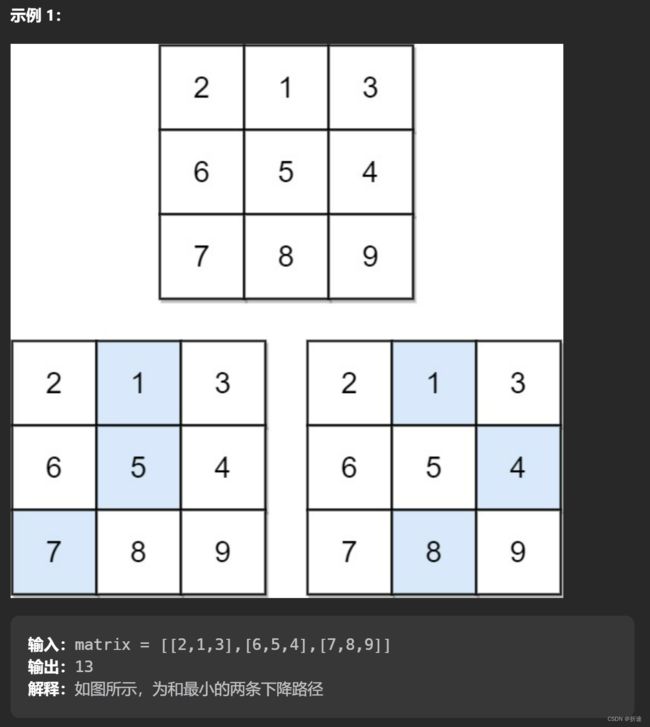
示例:

分析:

给我们一个矩阵,我们需要找出一条路径从矩阵第一层(索引为0)到达矩阵最后一层,并且使得路径上的数值之和最小.

如果是老手,那么应该一眼就能看出来可以使用动态规划,如果看不出来,那我们接下来一起分析分析.

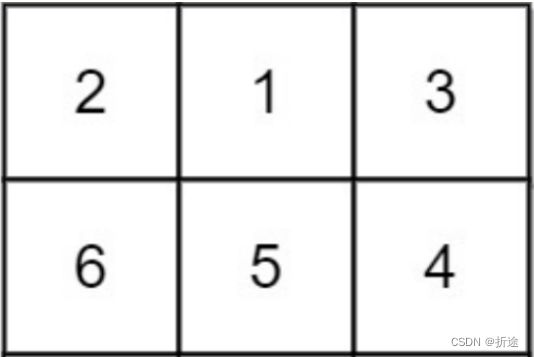
首先我们先不要搞这么复杂,以示例1为例,我们就假设矩阵只有两层,先忽略掉第三层(最后一层):

那么我们从第一层到达最后一层(第二层)的最短路径和是多少呢.

如果我到达的是第二层的6,那么我是可以从第一层的2和1两个地方到达,所以我们如果到达的地方是6,则最短路径和是1+6=7.

如果我到达的是第二层的5,那么可以从第一层的2和1和3一共三个地方到达,即到达第二层的5的最短路径和为1+5=6.同理,到达第二层的4的最短路径和为1+4=5.

所以如果是上述两层的矩阵,我们得到的最短路径和是5(从第一层到达最后一层的4).

我们现在再把第三层加入进来,是这样的:

 和我们刚才只有两层的矩阵相比,仅仅是多了一层,我们仍然可以套用刚才的计算公式,现在我们把刚刚推导出来的到达第二层的最短路径和覆盖掉原始的数值,是这样的:

 我们可以接着利用推导过的第二层来接着推导第三层,最后是这样的:

 

所以我们遍历最后推断完毕的最后一层可以得出示例1的最小路径和是13.

这类可以将大问题拆分成多个有关联性的小问题的题目,我们都可以使用动态规划.并且动态规划大多离不开贪心思想.

根据以上思路我们不难写出代码,但是有一点需要注意一下,就是在遍历矩阵每层的首位元素的时候要注意不能下标越界,具体可以参考下面的代码.

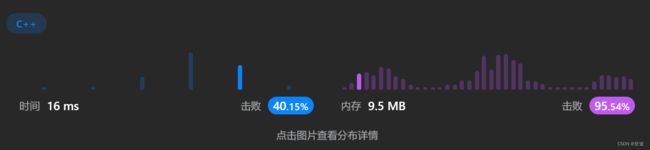
完整代码+结果如下:

class Solution {
public:
    int minFallingPathSum(vector>& matrix) {
        int n=matrix.size();
        if(n==1) return matrix[0][0];
        for(int i=1;i