机器学习(12)--K-Means
目录
一、聚类
二、机器学习中的距离
三、sklearn中的聚类算法
四、KMeans簇内平方和和时间复杂度
五、sklearn中的KMeans
1、建立一个数据集
2、使用K-Means进行聚类操作
3、根据上面的模型绘散点图观察分类效果。
4、评估指标
4.1对于真实标签已知情况
4.2当真实标签未知时:轮廓系数
4.3当真实标签未知时的其他指标
六、使用K-Means进行压缩图片
1、使用sklearn库自带的图片来压缩
2、将图片降维至二维
3、聚类
4、还原三维图片
5、采取随机选取64个数据来压缩进行对比
6、输出图片
一、聚类
聚类算法又叫做“无监督分类”,其目的是将数据划分成有意义或有用的组(或簇)。组内的对象之间是相关的,不同组之间是不相关的,组内的相关性越大,组间差异性越大,聚类特征越好。 聚类的中心称为簇心,表达簇内样本点的距离均值(欧式距离)
二、机器学习中的距离
1、欧氏距离:计算欧式空间中两点之间的距离,即直线距离.
欧氏距离计算公式:
![]()
2、曼哈顿距离:表明两个点在标准坐标系上的绝对轴距总和,就是离散的欧式空间。
曼哈顿距离计算公式:
![]()
3、闵可夫斯基距离:是对多个距离度量公式的概括性表述,是一组距离的定义,当公式中参数p=1时,为曼哈顿距离,当p=2时为欧几里得距离。
闵可夫斯基距离计算公式:
![]()
4、切比雪夫距离:L∞度量,是向量空间中的一种度量,表示两个点之间的距离定义是其各坐标数值差绝对值的最大值。可以参考国际象棋中王从一个位子移动至另一个位置可以有八个方向,距离均为1,而所有距离王的位置就是切比雪夫距离。
切比雪夫距离计算公式:
![]()
5、余弦距离:也称余弦相似度,机器学习中常用这一概念来衡量样本向量之间的差异,先比于上面的距离度量,余弦距离更注重两个向量在方向上的差异。
余弦距离计算公式:
三、sklearn中的聚类算法
聚类算法在sklearn中有类和函数两种表示方式,下面是类有关的部分聚类算法。
| 类 | 含义 |
| cluster.AffinityPropagation | 执行亲和传播数据聚类 |
| cluster.AgglomerativeClustering | 凝聚聚类 |
| cluster.Birch | Birch聚类 |
| cluster.DBSCAN | DBSCAN聚类 |
| cluster.FeatureAgglomeration | 凝聚特征 |
| cluster.KMeans | K均值聚类 |
| cluster.MiniBatchKMeans | 小批量K均值聚类 |
| cluster.MeanShift | 平坦核函数平均移位聚类 |
| cluster.SpectralClustering | 光谱聚类 |
KMeans:
聚类原则:以空间中k个点位中心进行聚类,对最靠近他们的对象进行归类,计算各簇中心的值为新的质心,并进行迭代更新,直至簇心位置不在改变,或达到最大迭代次数。
优点:速度快,且实现简单
缺点:对于混合度高的,非球状类簇聚类效果差。
容易陷入局部最优解,算法结果不稳定。
对于噪声或离群点较为敏感,难以区分噪声和离群点,导致聚类紧密程度降低。
DBSCAN:
聚类原则:基于密度可达关系,聚类距离簇边界最近的点。
优点:能够识别任意形状的样本,将具有足够密度的区域划分为簇。
缺点:需要指定最少点个数。
光谱聚类:
聚类原则:从图论中衍生出来的算法,吧所有数据看做空间中的点,将这些点用边连接起来,距离较远的两个点的边权重值较低,而距离较近的两个点之间的边权重值较高。并通过对所有数据点组成的图进行切图,对切图后不同的子图间边权重和尽可能的第,而子图内的边权重和尽可能的高,从而达到聚类。
四、KMeans簇内平方和和时间复杂度
KMeans使用的簇内平方和,是将一个数据集中所有簇的簇内平方和相加,又称total inertia。簇内平方和越小,聚类效果越好,但是由于这个评估指标没有边界,所以很难判断效果是否好。
KMeans有损失函数吗?
inertia更像是KMeans的模型评估指标,而非损失函数。由于KMeans不去求解参数,所以模型的本质也没有在拟合数据,更像是在探索数据本身。
KMeans的平均复杂度为O(k*n*T),其中k为输入的簇数,n为整个数据集的样本量,T为迭代次数。(相比于KNN的平均复杂度为O(n))。在最坏复杂度上可以达到![]() ,可以看到KMeans算法的计算速度非常之慢,所以在KMeans聚类的参数选择时会将训练策略默认为k-means++,而不会选取random。
,可以看到KMeans算法的计算速度非常之慢,所以在KMeans聚类的参数选择时会将训练策略默认为k-means++,而不会选取random。
五、sklearn中的KMeans
1、建立一个数据集
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import sklearn.metrics as mt
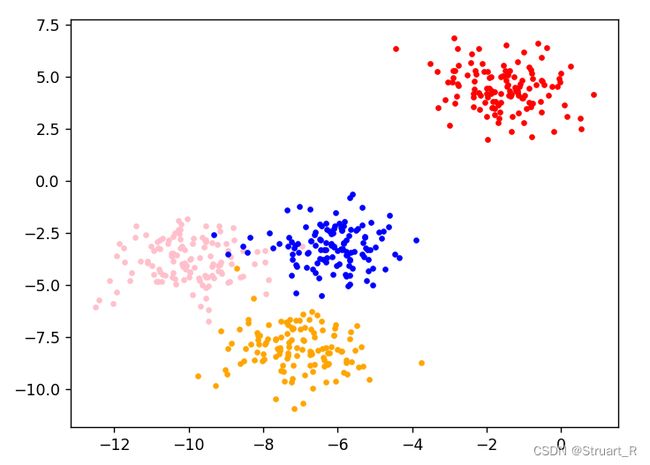
x,y=make_blobs(n_samples=500,n_features=2,centers=4,random_state=1) #建立一个500个样本的,特征数为2,4个簇的数据集
fig,ax1=plt.subplots(1)
color=["red",'pink',"orange","blue"]
for i in range(4):
ax1.scatter(x[y==i,0],x[y==i,1],marker='o',s=8,c=color[i]) #使用不同颜色标注4个种类绘制散点图
plt.show()2、使用K-Means进行聚类操作
首先假设有三个簇,由于聚类K-Means算法需要指定簇数,所以需要去找寻最优的簇数。
from sklearn.cluster import KMeans
n_clusters=3 #先假设有3簇,进行统计聚类
cluster=KMeans(n_clusters=n_clusters,init='random',random_state=0).fit(x)
print(cluster.n_iter_)
cluster=KMeans(n_clusters=n_clusters,random_state=0).fit(x) #init默认为kmeans++,迭代次数更少
print(cluster.n_iter_) #输出迭代次数
#print(cluster.labels_) #输出预测500个点聚类后的标签
pre=cluster.fit_predict(x) #由于预测也是输出标签所以与上面输出一致
#print(pre)输出KMeans模型的三个质心和簇内平方和 。
centroid=cluster.cluster_centers_
print(centroid) #质心
inertia=cluster.inertia_
print(inertia) #输出簇内平方和3、根据上面的模型绘散点图观察分类效果。
#画聚类训练后的图
y_pred=cluster.predict(x)
fig,ax1=plt.subplots(1)
color=["red",'pink',"orange","gray"]
for i in range(n_clusters):
ax1.scatter(x[y_pred==i,0],x[y_pred==i,1],marker='o',s=8,c=color[i])
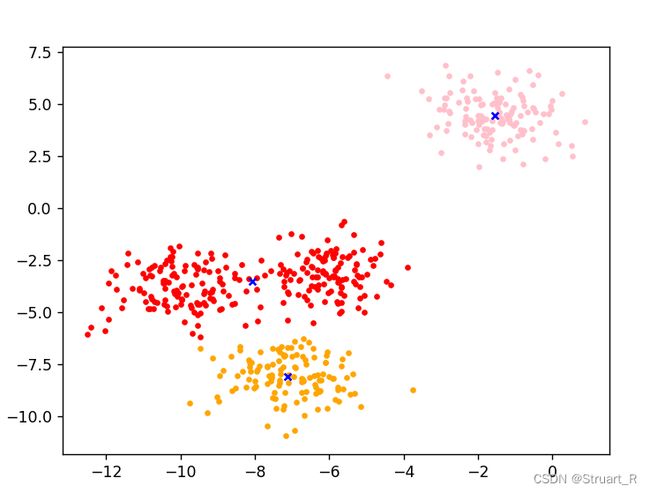
ax1.scatter(centroid[i,0],centroid[i,1],marker='x',s=20,c='b')
plt.show()
可以看到在分成3簇时,模型将中间两个靠的较近的分成了一个类,而距离较远的一组样本,可以很好地分成一个类。
4、评估指标
如何衡量聚类算法的效果?
对于KMeans的目标是簇内差异小,簇外差异大,可以通过衡量簇内差异来衡量聚类效果。
Inertia簇内平方和,为什么不能作为评估指标?
1、无界,不能进行比较
2、容易受到特征数目的影响,数据维度过大,容易陷入维度诅咒,计算量爆炸
3、容易收到超参数K的影响,即簇数影响,簇数越大Inertia会逐渐减小,趋于0
4、Inertia对于数据分布必须满足凸分布,且数据各向同性,但现实中的数据可能存在细长簇,环形簇,不规则形状流形,在这种分布下表现不佳。
4.1对于真实标签已知情况
y_pred就是指经过模型预测的标签,y_true就是真实标签,x是数据
| 模型评估指标 | 说明 | |
| 互信息分析 | 普通互信息分析 metrics.adjusted_mutual_info_score(y_pred,y_true) |
取值在(0,1)之间,越接近1,聚类效果越好 |
| 调整互信息分析 metrics.mutual_info_score(y_pred,y_true) |
||
| 标准化互信息分析 metrics.normalized_mutual_info_score(y_pred,y_true) |
||
| V-measure | 同质性:是否每个簇仅包含单个类的样本 metrics.homogeneity_score(y_true,y_pred) |
取值范围(0,1)之中,越接近1,聚类效果越好。 对样本分布没有假设,在任何分布都有不错表现 |
| 完整性:是否给定类的所有样本都分配给同一个簇中 metrics.completeness_score(y_true,y_pred) |
||
| 同质性和完整性的调和平均,叫做V-measure metrics.v_measure_score(labels_true,labels_pred) |
||
| 三者一次性计算出来 metrics.homogeneity_completeness_v_measure(labels _true,labels_pred) |
||
| 调整兰德系数 | 调整兰德系数 metrics_adjusted_rand_score(y_true,y_pred) |
取值在(-1,1)之间,负值象征着簇内的点差异巨大,甚至相互独立,正类的兰德系数比较优秀,越接近1越好。 对样本分布没有假设,在具有“折叠”形状的数据表现优秀。 |
4.2当真实标签未知时:轮廓系数
在现实中的数据来说,基本都是没有真实标签的数据进行探索,所以完全依赖于评价簇内的稠密程度和簇间的离散程度来评估聚类的效果好坏。轮廓系数作为最常用的评价指标,轮廓系数中有两个参数a和b。
a:样本与其自身所在的簇中其他样本的相似度为a,等于样本与同一簇中所有其他点之间的平均距离。
b:样本与其他簇中的样本的相似度为b,等于样本与下一个最近的簇中所有点之间的平均距离。
轮廓系数计算公式:
![]()
轮廓系数范围为(-1,1),s值趋近1,表示与自己所在的簇中样本很相似,并且与其他簇中的样本不相似。s值越趋近-1,则表示样本点与簇外的样本更加相似。若s值接近0,则表示两个簇中的样本基本相似,两个簇应为一个簇。
print(mt.silhouette_score(x,y_pred)) #注意是x和y_pred,轮廓系数(对每一个样本进行计算轮廓系数)输出为平均数,为一个数
print(mt.silhouette_samples(x,y_pred)) #输出对每一个样本计算轮廓系数的值轮廓系数也有缺陷,在凸型类上表现会呈现虚高,在基于密度进行的聚类和DBSCAN获得的聚类结果,也会产生虚高。
4.3当真实标签未知时的其他指标
| 卡林斯基-哈拉巴斯指数 metrics.calinski_harabaz_score(x,y_pred) |
| 戴维斯-布尔丁指数 metrics.davies_bouldin_score(x,y_pred) |
| 权变矩阵 metrics.cluster.contingency_matrix(x,y_pred) |
卡林斯基-哈拉巴斯指数没有范围,越高越好,计算公式如下:
![]()
其中N为数据集中的样本量,k为簇数,Bk为组间离散矩阵,即不同簇间的协方差矩阵,Wk是簇内离散矩阵,即一个簇内数据的协方差矩阵,Tr为矩阵的迹。
卡林斯基-哈拉巴斯指数,也会在凸型数据中产生虚高,但是时间要比轮廓系数快很多。
六、使用K-Means进行压缩图片
1、使用sklearn库自带的图片来压缩
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans #聚类
from sklearn.metrics import pairwise_distances_argmin #对两个序列中的点进行距离匹配的函数
from sklearn.datasets import load_sample_image #导入图片数据所用的类
from sklearn.utils import shuffle #打乱为什么要用sklearn啊
china=load_sample_image('china.jpg') #数据集中有china和flower两个图片
print(china.dtype) #uint8图片类型
print(china.shape) #(427,640,3)
newimage=china.reshape((427*640,3))
import pandas as pd
print(pd.DataFrame(newimage).drop_duplicates().shape) #减少重复,可以看到有9w多个像素构成图片2、将图片降维至二维
由于KMeans输入只有两个参数,所以将图片的长宽参数糅合为一维,保留颜色的维度
n_cluster=64
china = np.array(china,dtype=np.float64)/china.max() #归一化到0-1
w,h,d = original_shape = tuple(china.shape) #这种等号!!!
assert d==3 #防止d维度被改变,可以立即暂停
image_array = np.reshape(china,(w*h,d)) #reshape到二维
print(image_array.shape) #(273280,3)3、聚类
随机取出1000个数据来训练模型,用局部的结果来作为全部训练的结果,减少时间消耗,但一定是要花费一定的聚类效果的。
image_array_sample=shuffle(image_array,random_state=0)[:1000] #取出1000个来进行kmeans计算质心,生成64个质心
kmeans=KMeans(n_clusters=n_cluster,random_state=0).fit(image_array_sample) #kmeans
print(kmeans.cluster_centers_) #输出质心4、还原三维图片
labels=kmeans.predict(image_array) #用1000个点训练好的64簇的模型预测27w个点,输出labels为0-63的索引
print(labels.shape)
image_kmeans=image_array.copy()
for i in range(w*h):
image_kmeans[i]=kmeans.cluster_centers_[labels[i]] #将这27w个点中的上一行映射的索引,转换为这64个簇所对应的值
image_kmeans = image_kmeans.reshape(w,h,d) #reshape回到3个维度5、采取随机选取64个数据来压缩进行对比
#使用随机质心进行降维
centroid_random=shuffle(image_array,random_state=0)[:n_cluster] #随机找64个质心
labels_random=pairwise_distances_argmin(centroid_random,image_array,axis=0)
print(labels_random) #生成随机方式生成的不同数据与64个标签的映射关系
image_random=image_array.copy()
for i in range(w*h):
image_random[i]=centroid_random[labels_random[i]]
image_random=image_random.reshape(w,h,d)6、输出图片
#画出原图,随机质心,kmeans三个图
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('original image')
plt.imshow(china)
plt.savefig('origin.png')
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('k-means,64 colors')
plt.imshow(image_kmeans)
plt.savefig('k-means.png')
plt.figure(figsize=(10,10))
plt.axis('off')
plt.title('random,64 colors')
plt.imshow(image_random)
plt.savefig('random.png')
plt.show()通过聚类算法压缩图片后,相比于随机选取数据进行压缩,图片颜色上影响不会特别大。
参考视频:【sklearn机器学习】菜菜的sklearn机器学习完整版(中)_哔哩哔哩_bilibili
参考书籍:《机器学习》周志华