笔试强训 Day6
选择题
1.十进制变量i的值为100,那么八进制的变量i的值为()
A 146
B 148
C 144
D 142
本题很简单:100除8,取余数,直到商为零,最后反向的串起余数即可
2.执行下面语句后的输出为()
int I=1;
if(I<=0)
printf("****\n") ;
else
printf("%%%%\n");
A %%
B ****
C 有语法错,不能正确执行
D %%%%
3.对于下面的C语言声明描述正确的一项是()
char (*p)[16]
A p是长度为16的字符指针数组
B p是包含16个字符的字符串
C p是指向长度为16的字符数组的指针
D p是长度为16的字符数组
- p是一个指针,指向的是长度为16的字符数组 也叫作数组指针
4.数组a的定义语句为“float a[3][4];”,下列()是对数组元素不正确的引用方法
A a[i][ j]
B *(a[i]+j)
C *(*(a+i)+j)
D (a+i*4+j)
a[i]——> *(a+i) —— 访问数组的a的第i个元素
二维数组a中的每个元素都是一个一维数组,很明显ABC都正确
5.下面程序的输出结果是__________。
#include < iostream.h>
#define SQR(A) A*A
void main() {
int x=6,y=3,z=2;
x/=SQR(y+z)/SQR(y+z);
cout< < x< < endl;
}
A 5
B 6
C 1
D 0
- 考察宏,在预处理阶段将宏展开
- 注意注意先全部替换了再运算,不要自己口算
x/=SQR(y+z)/SQR(y+z) ==x/=3+2 * 3+2 /3+2*3+2=》x/=17=>x=6/17=0
6.当n=5时,下列函数的返回值是()
int foo(int n){
if(n<2){
return n;
}
else
return 2*foo(n-1)+foo(n-2);
}
A 5
B 11
C 29
D 10
- 考察递归算法,画递归图算出f1、f2、f3等的数值,最后相加即可
7.以下对C语言的”指针“描述不正确的是()
A 32位系统下任何类型指针的长度都是4个字节
B 指针的数据类型声明的是指针实际指向内容的数据类型
C 野指针是指向未分配或者已释放的内存地址
D 当使用free释放掉一个指针内容后,指针变量的值被置为NULL
B.int* p ----->p指向的是int类型的空间
C.int* p(int*)malloc(4); free(p)
free释放后,只是将p所在的内存空间释放了,并没有将p指针置为空,需要手动置空
8.数组定义为”int a[4][5];”, 引用”*(a+1)+2′′表示()(从第0行开始)
A a[1][0]+2
B a数组第1行第2列元素的地址
C a[0][1]+2
D a数组第1行第2列元素的值
(a+1)表示数组a中第一个元素的地址
*(a+1)表示数组a中第一个元素
*(a+1)+2是对一维数组后移两个单位;表示的是a数组第1行第2列元素的地址
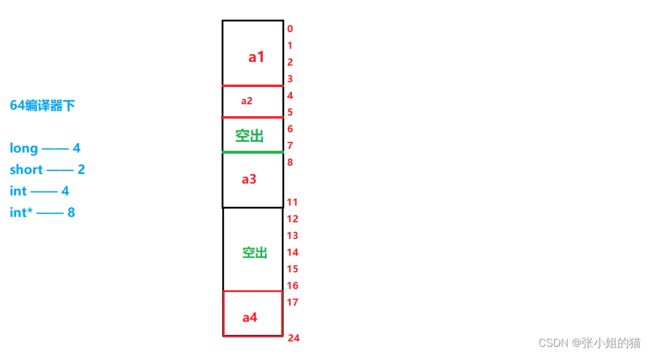
9.有一个如下的结构体:
struct A{
long a1;
short a2;
int a3;
int *a4;
};
A.24
B.28
C.16
D.18
10.运行结果是()
#include
using namespace std;
int f(int n){
if (n==1)
return 1;
else
return (f(n-1)+n*n*n);
}
int main(){
int s=f(3);
cout< A 8
B 9
C 27
D 36
本题考查的是递归,f(3)= f(2)+333;f(2)=f(1)+222;f(1)=1;因此f(3)=1+222+333=36
编程题:
不要二_牛客题霸_牛客网 (nowcoder.com)
思路:
在一个 W*H 的网格盒子中,最多可以放置多少块蛋糕的功能。下面是实现思路的解释:
- 首先,从输入中读取 W 和 H 的值,即网格盒子的宽度和高度。
- 创建一个二维向量
a,用于表示网格盒子,并将所有元素初始化为1。这里使用向量的向量来表示二维数组。- 对二维数组进行遍历,从左上角开始,依次处理每个网格的位置。
- 如果当前网格中放置了蛋糕(即元素值为1),则将计数器
count增加1,并且将当前网格右边和下面相邻的两个网格的元素值设置为0,表示这两个位置不能放置蛋糕。这样做的原因是,如果在当前位置放置了蛋糕,那么右边和下面相邻的两个位置就无法放置蛋糕,因为它们与当前位置的欧几里得距离为2。- 完成对网格盒子的遍历后,输出计数器
count的值,即最多可以放置的蛋糕数量。该实现思路通过遍历网格盒子的方式,按照一定规则放置蛋糕,以保证任意两块蛋糕之间的欧几里得距离不等于2。这样可以得到最多可以放置的蛋糕数量。代码中使用了向量的特性来表示二维数组,并且只遍历了一次网格盒子,所以时间复杂度为 O(W*H)。
代码实现:
#include
using namespace std;
#include
int main()
{
int W, H, count = 0;
cin >> W >> H;
//定义二维数组
vector> a;
//确定行
a.resize(W);
//确定列
for (auto& e : a)
{
//将每个元素初始化为1
e.resize(H, 1);
}
for (int i = 0; i < W; i++)
{
for (int j = 0; j < H; j++)
{
if (a[i][j] == 1)
{
count++;
if (i + 2 < W)
{
a[i + 2][j] = 0;
}
if (j + 2 < H)
{
a[i][j + 2] = 0;
}
}
}
}
cout << count << endl;
} 把字符串转换成整数__牛客网 (nowcoder.com)
代码实现1:
class Solution {
public:
int StrToInt(string str) {
if (str.empty()) {
return 0; // 如果字符串为空,返回0
}
int flag = 1; // 标志位,用于记录正负号,默认为正数
if (str[0] == '-') {
flag = -1; // 如果第一个字符是负号,将标志位设置为-1
str[0] = '0'; // 将负号替换为0,便于后续转换
}
else if (str[0] == '+') {
flag = 1; // 如果第一个字符是正号,将标志位设置为1
str[0] = '0'; // 将正号替换为0,便于后续转换
}
int sum = 0; // 用于累加转换后的结果
for (int i = 0; i < str.size(); i++) {
if (str[i] < '0' || str[i] > '9') {
sum = 0; // 如果遇到非数字字符,则将结果置为0
break;
}
else {
sum = sum * 10 + str[i] - '0'; // 将字符转换为数字,并累加到结果中
}
}
return flag * sum; // 返回带符号的结果
}
};
实现2:
#include
using namespace std;
class Solution {
public:
int StrToInt(string str) {
if (str.empty()) {
// 返回0或者抛出异常,表示输入为空字符串
return 0;
}
int flag = 1;
int sum = 0;
int i = 0;
if (str[0] == '+') {
flag = 1;
i++;
} else if (str[0] == '-') {
flag = -1;
i++;
}
for (; i < str.size(); i++) {
if (str[i] < '0' || str[i] > '9') {
// 非数字字符,返回0或者抛出异常,表示输入非法
return 0;
}
sum = sum * 10 + (str[i] - '0');
}
return sum * flag;
}
};