图像处理之高斯滤波

高斯函数

高斯函数广泛应用于统计学领域，用于表述正态分布，在信号处理领域，用于定义高斯滤波器，在图像处理领域，二维高斯核函数常用于高斯模糊Gaussian Blur，在数学领域，主要是用于解决热力方程和扩散方程，以及定义Weiertrass Transform。

1.一维高斯函数

高斯函数，Gaussian Function， 也简称为Gaussian，一维形式如下：
$$f(x)=a{e}^{-\frac{(x-b{)}^2}{2c^2}}$$
函数图像如下：

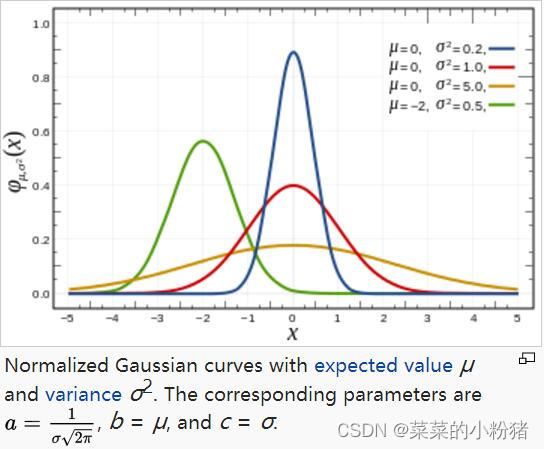
其中

• $a$表示曲线高度；
• $b(\mu )$表示曲线在$x$轴的中心；
• $c(\sigma )$表示半峰宽度有关；

2. 二维高斯函数

二维高斯函数在计算机视觉领域用处广泛，利用0均值的二维高斯函数,可以生成高斯卷积核，用于图像处理中的高斯滤波，实现高斯模糊，可以去除噪声。
公式如下：
$$G(x,y)=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{(x^2+y^2)}{2{\sigma }^2}}$$
三维立体图：

等高线图：

画图代码如下：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

# 定义二维高斯函数
def Gaussian(x, y, x0, y0, sigma):
    return np.exp(-((x - x0)**2 + (y - y0)**2) / (2.0 * sigma**2))

# 设置参数
sigma = 2
x, y = np.meshgrid(np.linspace(-5, 5), np.linspace(-5, 5))

# 计算高斯函数
z = Gaussian(x, y, 0, 0, sigma)

# 绘制3D图形
fig = plt.figure()
ax = Axes3D(fig)

#plt.get("可选参数如下")，可故意写错，报错可以提醒正确的配色
# 'Accent', 'Accent_r', 'Blues', 'Blues_r', 'BrBG', 'BrBG_r', 'BuGn', 'BuGn_r', 'BuPu', 'BuPu_r', 'CMRmap', 'CMRmap_r', 'Dark2', 'Dark2_r', 'GnBu', 'GnBu_r', 'Greens', 'Greens_r', 'Greys', 'Greys_r', 'OrRd', 'OrRd_r', 'Oranges', 'Oranges_r', 'PRGn', 'PRGn_r', 'Paired', 'Paired_r', 'Pastel1', 'Pastel1_r', 'Pastel2', 'Pastel2_r', 'PiYG', 'PiYG_r', 'PuBu', 'PuBuGn', 'PuBuGn_r', 'PuBu_r', 'PuOr', 'PuOr_r', 'PuRd', 'PuRd_r', 'Purples', 'Purples_r', 'RdBu', 'RdBu_r', 'RdGy', 'RdGy_r', 'RdPu', 'RdPu_r', 'RdYlBu', 'RdYlBu_r', 'RdYlGn', 'RdYlGn_r', 'Reds', 'Reds_r', 'Set1', 'Set1_r', 'Set2', 'Set2_r', 'Set3', 'Set3_r', 'Spectral', 'Spectral_r', 'Wistia', 'Wistia_r', 'YlGn', 'YlGnBu', 'YlGnBu_r', 'YlGn_r', 'YlOrBr', 'YlOrBr_r', 'YlOrRd', 'YlOrRd_r', 'afmhot', 'afmhot_r', 'autumn', 'autumn_r', 'binary', 'binary_r', 'bone', 'bone_r', 'brg', 'brg_r', 'bwr', 'bwr_r', 'cividis', 'cividis_r', 'cool', 'cool_r', 'coolwarm', 'coolwarm_r', 'copper', 'copper_r', 'cubehelix', 'cubehelix_r', 'flag', 'flag_r', 'gist_earth', 'gist_earth_r', 'gist_gray', 'gist_gray_r', 'gist_heat', 'gist_heat_r', 'gist_ncar', 'gist_ncar_r', 'gist_rainbow', 'gist_rainbow_r', 'gist_stern', 'gist_stern_r', 'gist_yarg', 'gist_yarg_r', 'gnuplot', 'gnuplot2', 'gnuplot2_r', 'gnuplot_r', 'gray', 'gray_r', 'hot', 'hot_r', 'hsv', 'hsv_r', 'inferno', 'inferno_r', 'jet', 'jet_r', 'magma', 'magma_r', 'nipy_spectral', 'nipy_spectral_r', 'ocean', 'ocean_r', 'pink', 'pink_r', 'plasma', 'plasma_r', 'prism', 'prism_r', 'rainbow', 'rainbow_r', 'seismic', 'seismic_r', 'spring', 'spring_r', 'summer', 'summer_r', 'tab10', 'tab10_r', 'tab20', 'tab20_r', 'tab20b', 'tab20b_r', 'tab20c', 'tab20c_r', 'terrain', 'terrain_r', 'turbo', 'turbo_r', 'twilight', 'twilight_r', 'twilight_shifted', 'twilight_shifted_r', 'viridis', 'viridis_r', 'winter', 'winter_r'
ax.plot_surface(x, y, z, rstride=2, cstride=2, cmap=plt.get_cmap('BuGn'))
plt.savefig('gaussianFunction.jpg')
plt.show()

# 绘制等高线图形
plt.contourf(x, y, z, 10, cmap=plt.get_cmap('PuOr'))
plt.savefig('gaussianContourf.jpg')
plt.show()

高斯滤波

1.高斯核生成

若要生成 $(2k+1)\ast (2k+1)$大小的高斯核，生成公式如下：
$$G[i,j]=\frac{1}{2\pi {\sigma }^2}{e}^{-\frac{((x-k-1{)}^2+(y-k-1{)}^2)}{2{\sigma }^2}}$$
其中 ${\sigma }_x={\sigma }_y=\sigma$
$$G_h[i,j]=\frac{G[i,j]}{sumG}(归一化)$$
其中 $sumG$为$G[i,j]$的和

2.滤波过程

图片来自于这里

下面是 5x5 ，σ=25高斯滤波器的实现代码：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import math
import cv2
import imgShow as iS
import random
# 去除噪音 - 使用 5x5 的高斯滤波器
def gaussianSmooth(img_gray):
    # 1.生成高斯滤波器/高斯核
    """
    要生成一个 (2k+1)x(2k+1)的高斯滤波器，滤波器的各个元素计算公式如下：2*k+1=5,k=2,
    H[i, j] = (1/(2\*pi\*sigma\*\*2))\*exp(-1/2\*sigma\*\*2((i-k-1)\*\*2 + (j-k-1)\*\*2))
    """
    sigma = 25
    gau_sum = 0
    gaussian = np.zeros([5, 5])
    for i in range(5):
        for j in range(5):
            gaussian[i, j] = math.exp((-1 / (2 * sigma * sigma)) * (np.square(i - 2) + np.square(j - 2)))
            gau_sum = gau_sum + gaussian[i, j]
    # 2.高斯滤波器归一化处理
    gaussian = gaussian / gau_sum
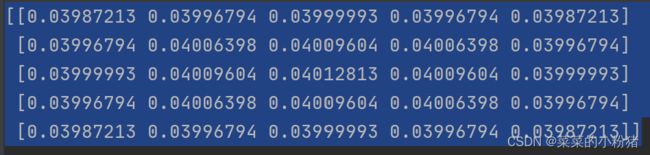
    print(gaussian)

    # 3.高斯滤波
    W, H = img_gray.shape
    new_gray = np.zeros([W , H])
    for i in range(W):
        for j in range(H):
            if(i<W-5 and j<H-5):
                new_gray[i,j] = np.sum(img_gray[i:i + 5, j:j + 5] * gaussian)
            else:
                new_gray[i,j] =img_gray[i,j]
    return new_gray


def gauss_noise(img, mean=0, sigma=25):
    image = np.array(img / 255, dtype=float)  # 将原始图像的像素值进行归一化
    # 创建一个均值为mean，方差为sigma，呈高斯分布的图像矩阵
    noise = np.random.normal(mean, sigma / 255.0, image.shape)
    out = image + noise  # 将噪声和原始图像进行相加得到加噪后的图像
    res_img = np.clip(out, 0.0, 1.0)
    res_img = np.uint8(res_img * 255.0)
    return res_img


img = cv2.imread('PeppersRGB.tif')
grayImg = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
noiseImg=gauss_noise(grayImg)
smoothImg = gaussianSmooth(grayImg)
iS.showImagegray(smoothImg, noiseImg, 25, 15, 'smoothImg', 'origin', './GaussianSmooth.jpg')
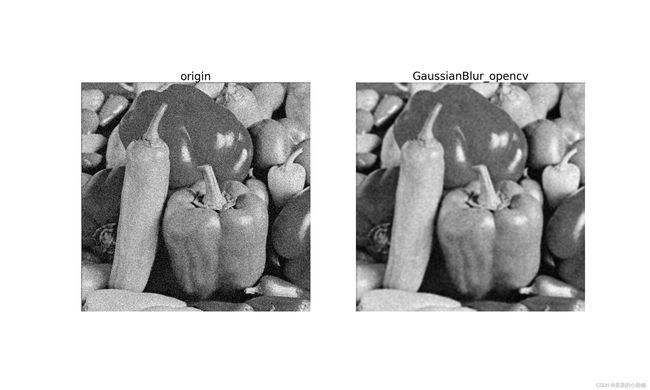
GaussianBlur_opencv=cv2.GaussianBlur(noiseImg,(5,5),25)
iS.showImagegray(GaussianBlur_opencv,noiseImg , 25, 15, 'GaussianBlur_opencv', 'origin', './GaussianSmooth_Opencv.jpg')

高斯核（归一化）显示结果

显示子图代码如下：

import matplotlib.pyplot as plt
#图像实际大小为 W*100 * H*100 像素  ,
def showImagegray(newImg,oldImg,W,H,newImgtitle,oldImgtitle,saveImgpath):

    plt.figure(figsize=(W,H))
    plt.subplot(121)
    plt.title(oldImgtitle,fontsize=30)
    plt.axis('off')
    plt.imshow(oldImg, cmap='gray')

    plt.subplot(122)
    plt.title(newImgtitle,fontsize=30)
    plt.axis('off')
    plt.imshow(newImg, cmap='gray')
    # plt.tight_layout()  # 调整整体空白
    plt.savefig(saveImgpath)
    plt.show()

代码效果如下：

点击这里整体代码可见github上代码
Opencv实现高斯滤波