【初识数据结构】手把手教会你时间复杂度的计算方法

前言 

大家好啊，这里是幸麟

一名普通的大学牲

希望可以不断的进步，因此也一直在学习

如果有写的不好或者写错的地方

欢迎在评论区指正

前言后的小前言

不知道在大家学习算法时有没有遇到这样一种情况，在看大佬题解或者讲解视频时

总能找到一个叫时间复杂度的词，比如O（n）的时间复杂度，O（nlogn）的时间复杂度

但这时间复杂度究竟是什么呢，他的好兄弟空间复杂度又是什么？（空间复杂度在写了在写了）

怀着这样的疑问，幸麟同学在学习了相关知识后写下了这篇博客

目录

时间复杂度

1.时间复杂度是什么？

2.时间复杂度怎么算？

大O的渐进表示法（时间复杂度的计算方法）

小结

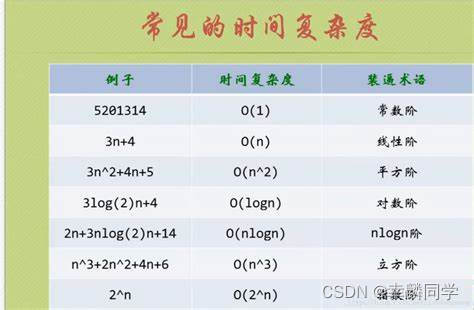
小结处附上了常见的时间复杂度表

---

---

时间复杂度

1.时间复杂度是什么？

我们可以先来看一下时间复杂度的定义：

时间复杂度是指在计算机科学与工程领域完成一个算法所需要的时间，是衡量一个算法优劣的重要参数。（来自百度百科）

我们可以姑且将其理解为，时间复杂度是一个可以计算算法运行时间的函数。可以让我们估计一个算法的大致运行时间

2.时间复杂度怎么算？

在学习时间复杂度的计算之前，我们要先知道时间复杂度是怎么样计算时间的

一般来说，一个程序的运行时间仅能通过上机运行来得到，而且不同的配置的计算机对同一程序进行运行，其运行时间也不会相同。

所以时间复杂度并不是直接对时间进行计算，而是通过计算算法中的基本操作的执行次数，来侧面对运行时间进行估算。

ps：算法中的基础操作有循环，判断这些，在时间复杂度计算时，我们一般拿循环次数作为评判标准

大O的渐进表示法（时间复杂度的计算方法）

1、如果一个算法的时间复杂度是一个常数（无论多大），我们都用1来进行表示，即O（1）

2、由于时间复杂度本身便是用来估算程序运行时间的，所以我们只保留最高阶项。

例如一个程序的基本操作的执行次数是n^2+n+10次，那么我们只保留最高项n^2，它的时间复杂度即是O（n^2）

3、如果最高阶项存在且不是1，则去除与这个项目相乘的常数。得到的结果就是大O阶。

例如：程序运行次数的最高阶项是10n，或者100000n，我们都认为其的时间复杂度是O（n）

同理，如果程序运行次数的最高阶项是n*(n-1)/2，我们都认为其的时间复杂度是O（n^2）

我们可以发现大O的渐进表示法去掉了那些对结果影响不大的项，简洁明了的表示出了执行次数。

另外有些算法的时间复杂度存在最好、平均和最坏情况：

最坏情况：任意输入规模的最大运行次数(上界)

平均情况：任意输入规模的期望运行次数

最好情况：任意输入规模的最小运行次数(下界)

例如：在一个长度为N数组中搜索一个数据x

最好情况：1次找到

最坏情况：N次找到

平均情况：N/2次找到

在实际中一般情况关注的是算法的最坏运行情况，

所以数组中搜索数据时间复杂度为O(N)

接下来我们实战运用一下：

请告诉我下面这一段代码的时间复杂度（答案后的黑条选中后可以查看）

void Func3(int N, int M)
{
 int count = 0;
 for (int k = 0; k < M; ++ k)
 {
 ++count;
 }
 for (int k = 0; k < N ; ++ k)
 {
 ++count;
 }
 printf("%d\n", count);
}

答案：O(N+M)，因为该代码循环了M+N次（M，N都是未知数）

对了，我好像忘了告诉你了，如果有两个未知数，要把两个未知数一起写上去的

至于为什么你通常看到的时间复杂度里的未知数都是N，这是因为N是大家约定好的默认未知数

如果同学你答对了，那么我们再来一个吧

请告诉我下面这一段代码的时间复杂度

int BinarySearch(int* a, int n, int x)
{
 assert(a);
 int begin = 0;
 int end = n-1;
 // [begin, end]：begin和end是左闭右闭区间，因此有=号
 while (begin <= end)
 {
 int mid = begin + ((end-begin)>>1);
 if (a[mid] < x)
 begin = mid+1;
 else if (a[mid] > x)
 end = mid-1;
 else
 return mid;
 }
 return -1;
}

答案：O(logN)

二分查找也存在最好、平均和最坏情况，这边我们用它最坏的情况来计算所以是O(logN)

（至于为什么最坏是logN可以去看一下其他博主的二分查找，当然以后我也会写的，但现在还没写好）

这边再介绍一下一个约定俗称的写法吧，如果一个算法的时间复杂度是一个以2为底的对数，我们一般不写底数，把原函数简写成logN，如果是以其他数为底的对数，那么那个底数是需要写出来的。

小结

时间复杂度计算的是一个算法中的基本操作的执行次数，它的计算遵循大O的渐进表示法

常见的时间复杂度：

好了，本文到这里就结束了，如果觉的这位幸麟同学写的还可以的话，不妨点个赞和关注，支持一下新人博主，谢谢了