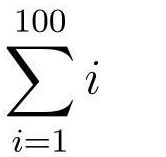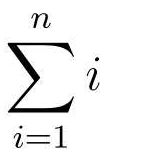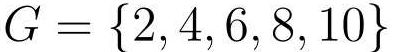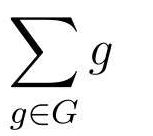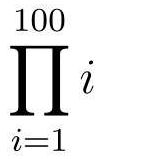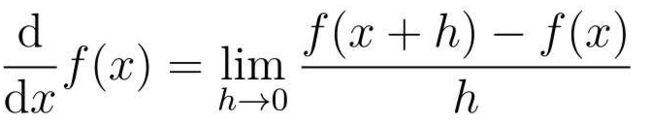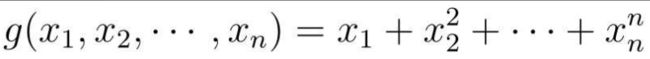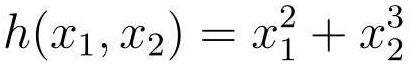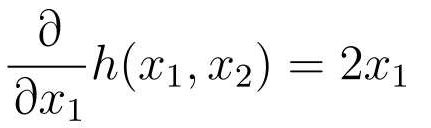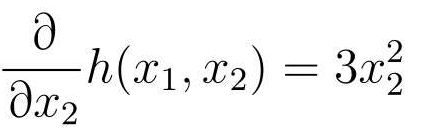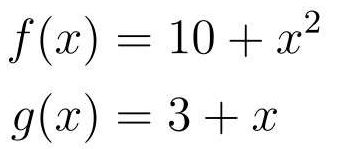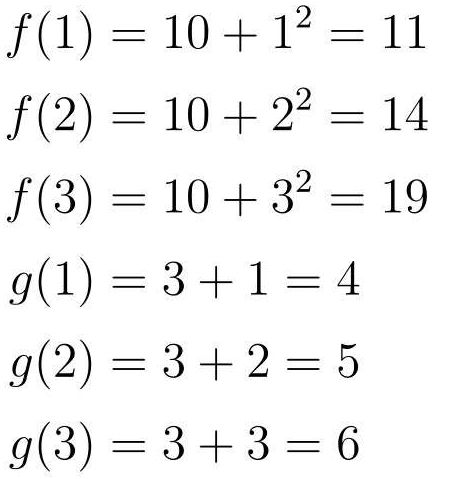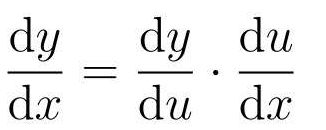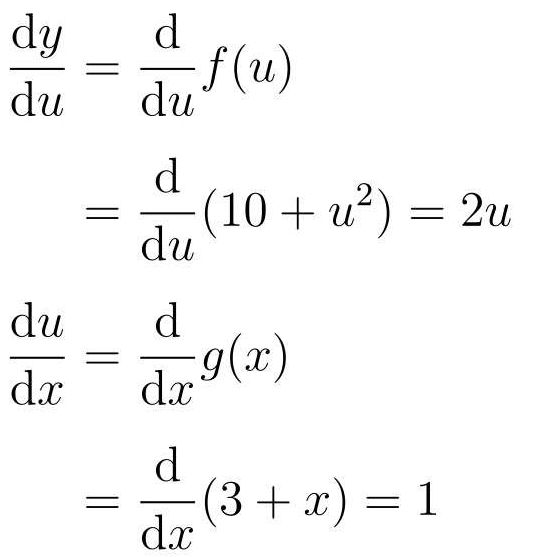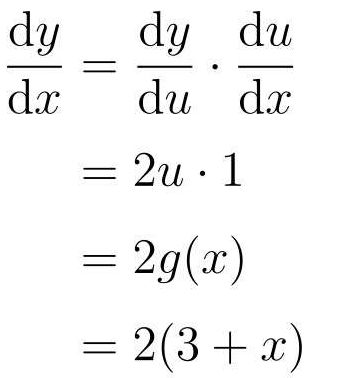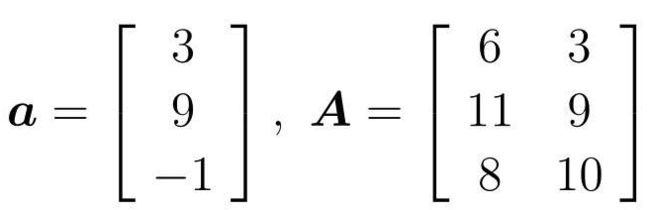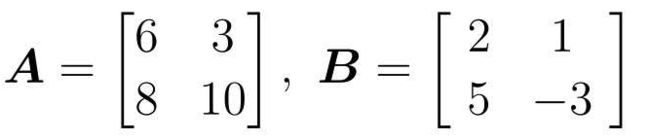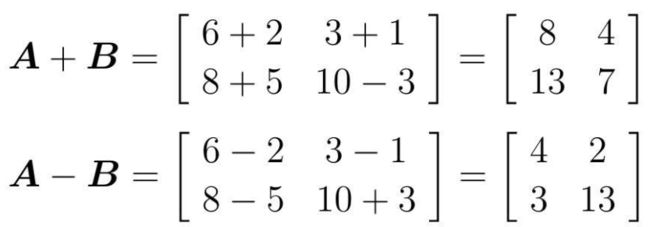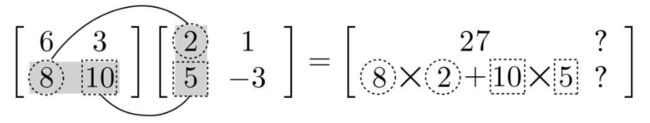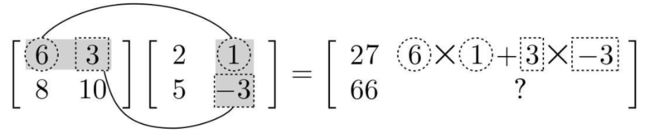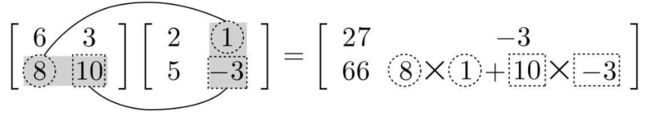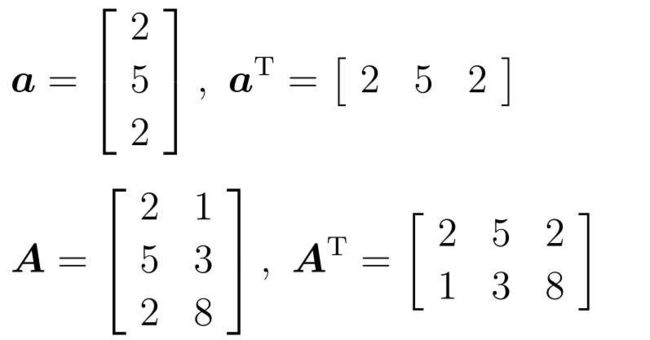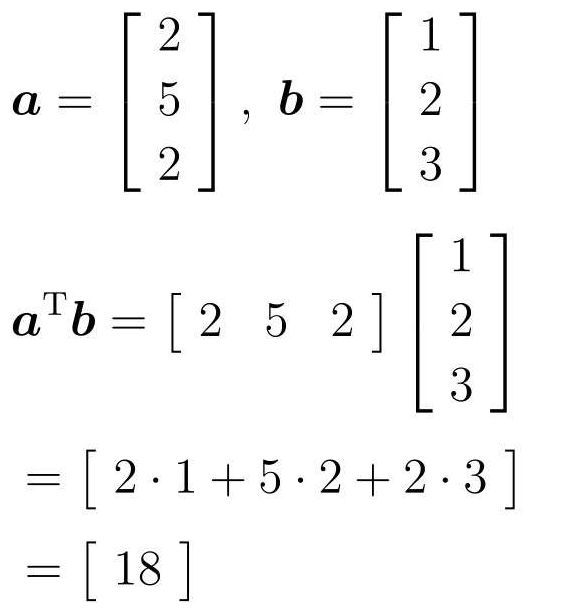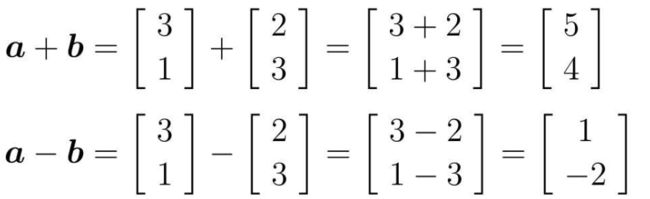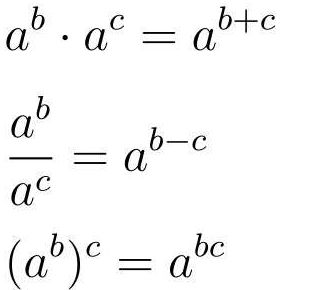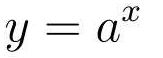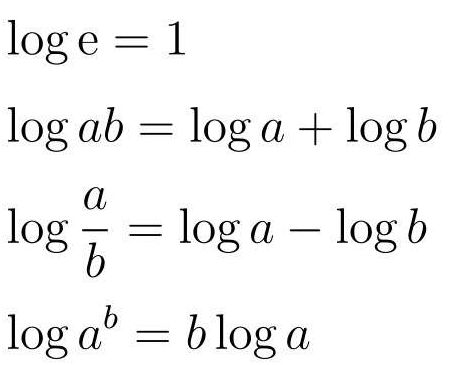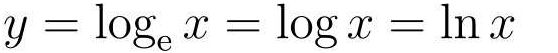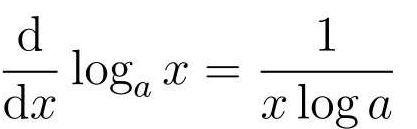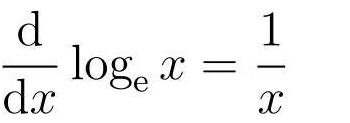一、机器学习前的数学基础知识
你说春天太短
还未来得及看见自己
就要粉碎成灯红酒绿的夏
那就开花呀
开他妈的
1. 求和、求积
1.1 求和
假设现在我们要在纸上写下1加到100的简单求和运算:
1 + 2 +3 + 4 + 5 + ........ + 99 + 100
使用求和符号简化(读作“西格玛”):
对于不明确要加到多少的情况:
对集合使用求和符号:
1.2 求积
假设现在我们要在纸上写下1乘到100的简单求积运算:
1 * 2 * 3 * 4 * 5 * ........ * 99 * 100
使用求积符号简化(读作“派”):
对于不明确要乘到多少的情况:
2. 微分
2.1 微分介绍
在机器学习领域,有很多用来解决最优化问题的方法,其中之一就是使用微分。
通过微分,可以知道函数在某个点的斜率,也可以了解函数在瞬间的变化。
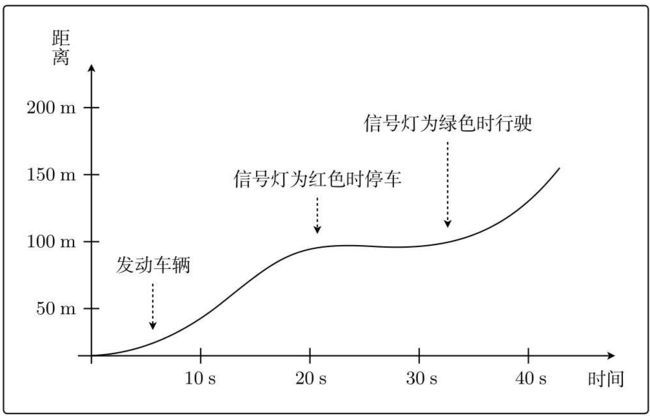
示例:开车行驶在大街上的场景(走走停停)
由整个图可以看出,车子在40s内大约行驶了120m,所以这一期间车辆的行驶速度:
120m / 40s = 3m/s
3m/s是车辆的平均速度,从图中可以看出,车子在刚启动时速度慢,且在红灯时速度变为0,即车辆在各个点的时间点的瞬时速度都取值不同。
为了求车辆的“瞬时速度”,我们来渐渐缩小时间间隔。
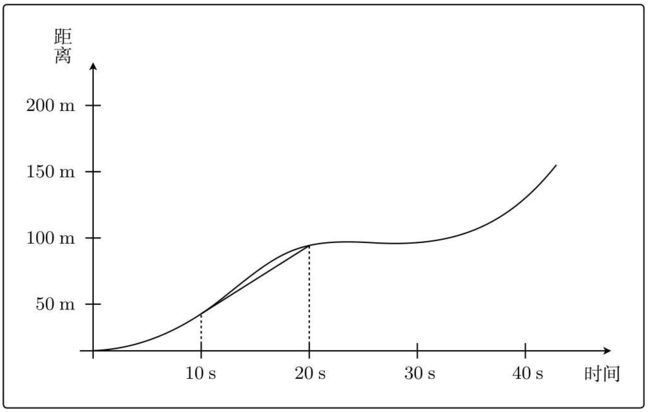
可以计算车辆在10s - 20s内的速度:
60m / 10s = 6m/s
同样,一次次缩小时间间隔,求10s - 11s之间的斜率,求10.0s - 10.1s之间的斜率。最后就可以得出10s那一瞬间的斜率,也就是速度。像这样缩小间隔求斜率的方法正是微分。
为了求这种“瞬时变化量”,假设函数为f(x),h为微小的数,那么函数f(x)在点x的斜率就可以表示为:
3. 偏微分
在前面的微分中,函数f(x)是只有一个变量x的单变量函数。但是,在实际工作中,是存在多个变量的多变量函数。
怎么来处理多变量函数?
核心:只需要关注微分的变量,把其他变量当作常数来处理,这种微分方法就称为偏微分。
示例:
函数h对x1的偏微分:
函数h对x2的偏微分:
像这样只关注要微分的变量,将其它变量全部作为常数来处理,就可以知道在这个变量下的斜率是多少。不管变量增加到多少,这个方法都是适用的。
4. 复合函数
有下面两个函数:
像x中代入任意值,可以得到函数的输出值:
不仅能像函数中代入常数,还可以代入函数进行计算:
像上面这种由多个函数组成的函数被称为复合函数。
示例:复合函数f(g(x))对x求微分
1. 把函数暂时替换为变量:
2. 分步骤进行微分:
也就是说,把y对u微分的结果与u对x微分的结果相乘即可。
3. 实际微分:
总结: 对复杂的函数进行微分,可以把函数当作多个简单函数组成而成的符合函数再进行微分,其中关键部分就是如何将函数分割为简单函数。
5. 向量和矩阵
向量就是把数字纵向排列的数据结构。
矩阵是把数字纵向和横向排列的数据结构。
常用小写字母表示向量,大写字母表示矩阵,并且都用黑体。
矩阵分别支持和、差、积的计算。假设有以下两个矩阵A和B,分别来计算一下它的和、差、积。
计算和、差:
计算积:需要将左侧矩阵的行与右侧矩阵的列的元素依次相乘,然后将结果加在一起。
最终结果:
最后,了解一下转置,交换行和列的操作就叫转置。
在计算向量的积时,经常会向下面一个向量转置之后再计算:
6. 几何向量
向量拥有大小和方向:
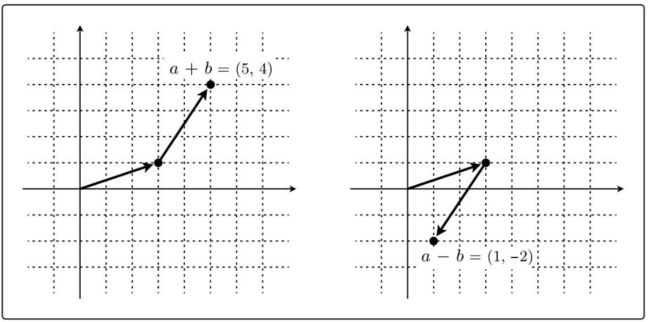
向量的加法和减法:
计算在代数上只是做了向量中各元素的相加和相减:
向量之间的积:
像这样,计算向量内积之后得到的已经不是向量,而是普通的数字(大小)了。这种普通数字有一个稍微生僻一点的叫法——标量。所以内积也可以被称为标量积。另外,由于内积的运算符号不是乘法符号“×”,而是点“·”,所以有时它也被称为点积。
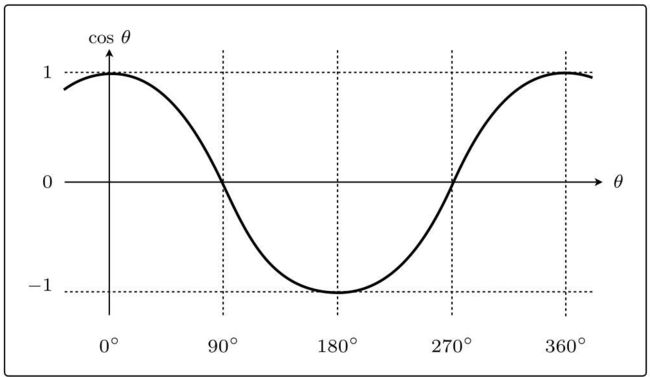
假设向量a和b之间的夹角为θ,那么内积也可以这样表示:
设θ为横轴、cosθ为纵轴,那么cos函数的图形如图:
法线向量指的是与某条直线相垂直的向量:
7. 指数与对数
指数法则
指数函数
对数法则
对数函数
自然对数
对数微分