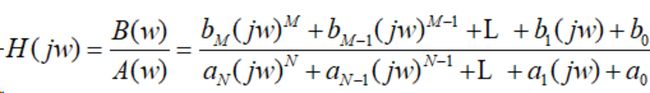信号与系统课程实验报告： 连续信号及其傅里叶变换的编程

一、实验目的

1. 认识并熟悉Matlab软件的使用，并能利用其进行编程
2. 利用Matlab实现连续信号的表示
3. 掌握数值法和符号法进行编程
4. 实现连续周期信号的傅里叶级数求解编程算法
5. 实现连续信号的傅里叶变换求解编程算法
6. 理解Matlab代码的具体意义并熟练使用
7. 利用Matlab对LTI系统的频率特性进行分析

 

二、实验内容

1. 正弦信号的Matlab编程及波形表示方法
2. 抽样信号的Matlab编程及波形表示方法
3. 复指数信号的Matlab的编程及波形方法
4. 连续周期信号的傅立叶变换的编程及波形表示方法
5. 连续信号的傅里叶变换的编程及波形表示方法
6. 利用Matlab分析LTI系统的频率特性

 

三、实验原理

1.连续信号的MATLAB表示

自变量在整个连续区间内都有定义的信号，称为连续时间信号，简称连续信号。从严格意义上来讲,MATLAB数值计算的方法并不能处理连续信号。然而，可以利用连续信号在等时间间隔点的取样值来近似表示连续信号，即当取样时间间隔足够小时，这些离散样值能被MATLAB所处理，并且能够较好地近似表示连续信号。

2.Matlab提供了大量生成基本信号的函数

如：

(1)指数信号：K*exp(a*t)

(2)正弦信号：K*sin(w*t+phi)和K*cos(w*t+phi)

(3)复指数信号：K*exp((a+i*b)*t)

(4)抽样信号：sin(t*pi)

(5)矩形脉冲信号：rectpuls(t,width)

(6)周期矩形脉冲信号：square(t,DUTY)，其中DUTY参数表示信号的占空比DUTY%，即在一个周期脉冲宽度(正值部分)与脉冲周期的比值。占空比默认为0.5。

(7)三角波脉冲信号：tripuls(t, width, skew)，其中skew取值范围在-1~+1之间。

(8)周期三角波信号：sawtooth(t, width)

3.Matlab中提供了常用的图形控制函数

1)利用clc, dir(ls), help, clear, format,

hold, clf控制命令的使用和M文件编辑/调试器使用操作；

2)主函数函数的创建和子程序的调用；

3)plot,subplot, grid on, figure, xlabel,ylabel,title,hold,title,Legend,绘图函数使用;

axis([xmin,xmax,ymin,ymax])：图型显示区域控制函数，其中xmin为横轴的显示起点，xmax为横轴的显示终点，ymin为纵轴的显示起点，ymax为纵轴的显示终点。

有时，为了使图形具有可读性，需要在所绘制的图形中，加上一些网格线来反映信号的幅度大小。MATLAB中的grid on/grid off可以实现在你的图形中加网格线。

grid on：在图形中加网格线。

grid off：取消图形中的网格线。

function y = delta(t)

dt = 0.01;

y = (u(t)-u(t-dt))/dt;

产生单位阶跃信号的扩展函数为：

% Unit step function

function y = u(t)

y = (t>=0); % y = 1 for t > 0, else y = 0

四、实验仪器

1. macOS（带有虚拟机）
2. Matlab软件

 

五、连续信号的编程实验代码及结果

1.正弦信号的Matlab编程及波形表示方法

（1）由于正弦信号在Matlab中用sin函数表示，于是调用格式：

ft=A*sin(w*t+phi)

（2）Matlab编程代码如下：

A=3; w=0.5*pi; phi=0;

t=0:0.01:8;

ft=A*sin(w*t+phi);

plot(t,ft);

grid on;

（3）正弦信号波形

 

2.抽样信号的Matlab编程

（1）抽样信号Sa(t)=sin(t)/t在Matlab中用sinc函数表示名，调用格式为：

Ft=sinc(t/pi)

（2）Matlab编程代码

t=-3*pi:pi/100:3*pi;

ft=sinc(t/pi);

plot(t,ft);

grid on;

axis([-10,10,-0.5,1.2]);    %定义画图范围，横轴，纵轴

title('抽样信号')         %定义图的标题名字

（3）抽样信号波形

3.复指数的Matlab编程及波形表示方法

（1）在Matlab中，复指数信号的调用格式为exp((a+j*w)*t)

（2）Matlab编程代码

t=0:0.01:5;

a=0.5;

w=8;

X= 2*exp((a+j*w)*t);

Xr=real(X);         %取实部   

Xi=imag(X);        %取虚部

Xa=abs(X);        %取模

Xn=angle(X);        %取相位

subplot(2,2,1),plot(t,Xr),axis([0,5,-(max(Xa)+0.5),max(Xa)+0.5]),title('real');

subplot(2,2,3),plot(t,Xi),axis([0,5,-(max(Xa)+0.5),max(Xa)+0.5]),title('imag');

subplot(2,2,2), plot(t,Xa),axis([0,5,0,max(Xa)+1]),title('abs');

subplot(2,2,4),plot(t,Xn),axis([0,5,-(max(Xn)+1),max(Xn)+1]),title('angle');

（3）复指数信号波形

 

4.连续周期信号的傅里叶级数的编程及表示方法

1. 连续周期信号的傅里叶级数

三角函数形式的傅里叶级数：

指数形式的傅里叶级数：

 

（2）Matlab编程代码

syms t n y

T=10;                                                   %设置周期

tao=1;     %设置脉宽

Nn=16; %输出数据位数为16

Nf=30; %谐波次数30

y=1; %主周期波形

a0=2*int(y,t,-tao/2,tao/2)/T; %直流分量

as=int(2*y*cos(2*pi*n*t/T)/T,t,-tao/2,tao/2); %余弦项系数

bs=int(2*y*sin(2*pi*n*t/T)/T,t,-tao/2,tao/2); %正弦项系数

an(1)=double(vpa(a0,Nn));

for k=1:Nf

    an(k+1)=double(vpa(subs(as,n,k),Nn));

    bn(k+1)=double(vpa(subs(bs,n,k),Nn));

end %符号量转数值量

cn=sqrt(an.*an+bn.*bn); %幅度谱

for i=0:Nf

    if an(i+1)>=0

        phase(i+1)=0;

    else

        phase(i+1)=pi;

    end

end %相位谱

subplot(211);

k=0:Nf;

stem(k,cn);

subplot(212)

stem(k,phase);

（3）波形表示：幅度谱与相位谱

六、连续信号傅里叶变换的编程实验

 

1.傅里叶变换及其逆变换表达式

 

2.傅里叶变换的Matlab求解

Matlab的symbolic Math Toolbox提供了直接求解傅立叶变换及其逆变换的函数fourier()及ifourier()，两者的调用格式如下：

（1）Fourier 变换的调用格式

F=fourier(f)：它是符号函数f的fourier变换默认返回是关于w的函数。

F=fourier(f，v):它返回函数F是关于符号对象v的函数，而不是默认的w，即

（2）Fourier逆变换的调用格式

f=ifourier(F):它是符号函数F的fourier逆变换，默认的独立变量为w，默认返回是关于x的函数。

f=ifourier(f,u):它的返回函数f是u的函数，而不是默认的x.

注意：在调用函数fourier()及ifourier()之前，要用syms命令对所用到的变量(如t,u,v,w)进行说明,即将这些变量说明成符号变量。

3.具体连续信号Matlab编程代码及波形

（1）求解f(t)=exp(-6|t|)的傅里叶变换

syms t

f=exp(-2*abs(t))

F=fourier(f)

F=4/(4+w^2)

运算结果如下：

0.0588

 

（2）求解单边指数信号f(t)=exp(-6t)*u(t)的傅里叶变换

具体代码：

syms t phase im re

%f=exp(-6*t)*sym(‘Heaviside(t)’);   % Heaviside(t)第一个字母要小写

f= exp(-6*t)* heaviside(t);   % Heaviside(t)第一个字母要小写

F=fourier(f);

% im=image(F); %计算F的实部

im=imag(F); %计算F的实部

re=real(F); %计算F的虚部

phase=atan(im/re); %计算相位

subplot(211);

ezplot(abs(F)); %绘制幅度谱

subplot(212);

ezplot(phase); %绘制相位谱

 

幅度谱与相位谱如下

 

4.利用Matlab分析LTI系统的频率特性

当系统的频率响应H(jw)是jw的有理多项式时，有

 

MATLAB信号处理工具箱提供的freqs函数可直接计算系统的频率响应的数值解。

其调用格式如下

H=freqs(b,a,w)

其中，a和b分别是H(jw)的分母和分子多项式的系数向量，w为形如w1:p:w2的向量，定义系统频率响应的频率范围，w1为频率起始值，w2为频率终止值,p为频率取样间隔。

H返回w所定义的频率点上，系统频率响应的样值。

（1）三阶归一化的butterworth 低通滤波器的频率响应为

 

画出系统的幅度响应和相位响应

I具体代码：

w=0:0.025:5;

b=[1];a=[1,2,2,1];

H=freqs(b,a,w)

subplot(2,1,1);

plot(w,abs(H));grid;

xlabel('\omega(rad/s)');

ylabel('|H(j\omega)|');

title('H(jw)的幅频特性');

subplot(2,1,2);

plot(w,angle (H));grid;

xlabel('\omega(rad/s)');

ylabel('\phi(\omega)');

title('H(jw)的相频特性');

幅频特性与相频特性

 

七、实验心得及体会

1. 本次实验是首次利用Matlab软件进行代码的编写及波形的绘制，为了能更高效更有目的性地完成本次实验，在进行实验前花了一段时间利用网上的Matlab教程完成了Matlab的入门学习。学习的主要内容有Matlab界面介绍、基础编程操作、路径管理、绘图操作等等。
2. 通过此次实验学会了使用Matlab代码表示连续信号的方法、掌握了数值法和符号法进行编程以及各种波形的表示方法。最后理解了Matlab代码的具体意义并能够熟练运用。
3. 从实验开始，到最后结束，出现的最多的问题就是对软件操作的不熟练，最开始是体现在文件的新建方面。
4. 在编写代码时，时常未注意到中文符号和英文符号，导致调试系统时出现报错，又或者是在代码中无意添加了中文，如下样式

（1）在编写时由于参数设置的不精确，使波形一直都未出现，在多次调试后，波形才如愿得到。

（2）经过反复对代码的摸索、编写、改动，在实验中熟练掌握了Matlab函数的用法，对其也有了更深的理解。

（3）编写代码的时候必须细心。实验中在编写傅立叶变换的代码时，由于搞混了每个函数的作用区间，导致迟迟没有波形图出现，后经过多次调试才发现问题的根源。

（4）学习信号与系统的过程中，对于幅频特性和相频特性的理解一直都比较模糊。通过此次实验，编写具体代码得到相关信号的幅频特性和相频特性图，并进行对比学习，我觉得对这部分的知识有了更深的认识！

八、实验总结

通过本次实验，我学习到并熟练掌握了利用Matlab进行编程的方法，并能够进行连续信号及其傅里叶变换的编程及绘制。在实验的过程中，通过对波形的观察，更加深入地理解正弦函数、抽样函数和复指数函数的实质。在第4、5个分实验中，进行了对连续周期函数傅立叶级数的计算和对连续函数傅立叶变换的求解，此过程让我对课本上关于幅度谱和相位谱的理解更为深刻，最后一个实验中，利用Matlab对LTI系统的频率特性进行分析，通过编写代码，函数傅立叶变换的幅频特性和相频特性直接呈现出来，清晰明了！

2023-02-11