13年12月CCF计算机软件能力认证(csp认证) 内有c++和Python代码

第一题：出现次数最多的数

给定 n 个正整数，找出它们中出现次数最多的数。

如果这样的数有多个，请输出其中最小的一个。

输入格式

输入的第一行只有一个正整数 n，表示数字的个数。

输入的第二行有 n 个整数 s1,s2,…,sn。

相邻的数用空格分隔。

输出格式

输出这 n 个次数中出现次数最多的数。

如果这样的数有多个，输出其中最小的一个。

数据范围

1≤n≤1000,
1≤si≤10000

输入样例：

6
10 1 10 20 30 20

输出样例：

10

 解题思路：使用哈希表统计每一个元素出现的次数，在统计的过程中即可求出最大值和最大值所对应的个数。

以下是代码：

c++

#include
#include

using namespace std;

const int N = 1e5 + 10;
int a[N];
int res = 0 , cnt = 0;
int n;

int main()
{
    memset(a , 0 , sizeof a);
    cin >> n;
    for(int i = 0;i < n;i ++)
    {
        int x;
        cin >> x;
        a[x] ++;
        if(a[x] > cnt) res = x , cnt = a[x];
        else if (a[x] == cnt)
        {
            if(x < res) res = x;
        }
    }
    cout << res << endl;
    return 0;
}

Python3

from collections import Counter
n = int(input())
d = Counter(list(map(int , input().split())))
res , cnt = 0x3f3f3f3f , -1
for i , j in d.items():
    if j > cnt:
        res , cnt = i , j
    elif j == cnt and res > i:
        res , cnt = i , j
print(res)

第二题： ISBN号码

每一本正式出版的图书都有一个 ISBN 号码与之对应。

ISBN 码包括 9 位数字、1 位识别码和 3 位分隔符，其规定格式如 x-xxx-xxxxx-x，其中符号 - 是分隔符（键盘上的减号），最后一位是识别码，例如 0-670-82162-4 就是一个标准的ISBN码。

ISBN 码的首位数字表示书籍的出版语言，例如 0 代表英语；第一个分隔符 - 之后的三位数字代表出版社，例如 670 代表维京出版社；第二个分隔之后的五位数字代表该书在出版社的编号；最后一位为识别码。

识别码的计算方法如下：

首位数字乘以 1 加上次位数字乘以 2……以此类推，用所得的结果 mod11，所得的余数即为识别码，如果余数为 10，则识别码为大写字母 X。

例如 ISBN 号码 0-670-82162-4 中的识别码 44 是这样得到的：对 067082162 这 9 个数字，从左至右，分别乘以 1,2,…,9，再求和，即 0×1+6×2+……+2×9=158，然后取 158mod11的结果 4 作为识别码。

编写程序判断输入的 ISBN 号码中识别码是否正确，如果正确，则仅输出 Right；如果错误，则输出是正确的 ISBN 号码。

输入格式

输入只有一行，是一个字符序列，表示一本书的 ISBN 号码（保证输入符合 ISBN 号码的格式要求）。

输出格式

输出一行，假如输入的 ISBN 号码的识别码正确，那么输出 Right，否则，按照规定的格式，输出正确的 ISBN 号码（包括分隔符 -）。

输入样例1：

0-670-82162-4

输出样例1：

Right

输入样例2：

0-670-82162-0

输出样例2：

0-670-82162-4

解题思路：进行模拟即可，将每一个数字截取出来，进行题目的运算，最后进行判断即可得到最终结果。

以下是代码：

c++

#include

using namespace std;

string s;
int check;
int now = 0 , cnt = 1;
long long res = 0;

int main()
{
    cin >> s;
    check = s[s.size() - 1] - '0';
    while(now < s.size() - 2)
    {
        if(s[now] == '-')
        {
            now ++;
            continue;
        }
        else
        {
            res += (s[now] - '0') * cnt;
            now ++ , cnt ++;
        }
    }
    if((res % 11 == 10 && check == 'X' - '0') || res % 11 == check) puts("Right");
    else 
    {
        if(res % 11 == 10) cout << s.substr(0 , s.size() - 1) + 'X';
        else cout << s.substr(0 , s.size() - 1) + to_string(res % 11);
    }
}

Python3

l = list(input().split('-'))
now , res = 1 , 0
for i in range(3):
    for j in l[i]:
        res += (ord(j) - ord('0')) * now
        now += 1
if l[-1] == 'X':
    if res % 11 == 10:
        print('Right')
    else:
        l[-1] = str(res % 11)
        print('-'.join(l))
else:
    if res % 11 == int(l[-1]):
        print("Right")
    else:
        l[-1] = str(res % 11) if res % 11 != 10 else 'X'
        print('-'.join(l)) 

第三题：最大的矩形

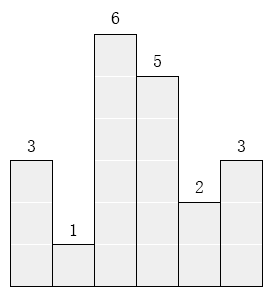
在横轴上放了 n 个相邻的矩形，每个矩形的宽度是 1，而第 i（1≤i≤n）个矩形的高度是 hi。

这 n 个矩形构成了一个直方图。

例如，下图中六个矩形的高度就分别是 3,1,6,5,2,3。

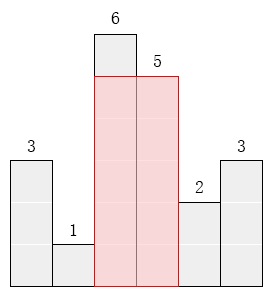
请找出能放在给定直方图里面积最大的矩形，它的边要与坐标轴平行。

对于上面给出的例子，最大矩形如下图所示的阴影部分，面积是 10。

输入格式

第一行包含一个整数 n，即矩形的数量。

第二行包含 n 个整数 h1,h2,…,hn，相邻的数之间由空格分隔。hi 是第 i 个矩形的高度。

输出格式

输出一行，包含一个整数，即给定直方图内的最大矩形的面积。

数据范围

1≤n≤1000,
1≤hi≤10000
经实测 hi 在官网的实际范围是 1≤hi≤40000

输入样例：

6
3 1 6 5 2 3

输出样例：

10

解题思路：进行模拟即可，对于每一个矩形，统计左右两边相邻的不超过该矩形高度的矩形个数即可，最终高度X个数取最大即可得到最终答案。

以下是代码：

c++

#include

using namespace std;

const int N = 1010;
int n;
long long h[N];
long long res = -1;

int main()
{
    cin >> n;
    for(int i = 0;i < n;i ++) cin >> h[i];
    
    for(int i = 0;i < n;i ++)
    {
        int l , r;
        
        for(int j = i;j >= 0;j --)
            if(h[j] >= h[i]) l = j;
            else break;
        
        for(int j = i;j <= n;j ++)
            if(h[j] >= h[i]) r = j;
            else break;
        
        // cout << h[i] << " " << l << " " << r << endl;
        res = max(res , h[i] * (r - l + 1));
    }
    cout << res << endl;
}

Python3

n = int(input())
h = list(map(int , input().split()))
res = 0
for i in range(n):
    l , r = i , i
    while l >= 0 and h[l] >= h[i]:l -= 1
    while r < n and h[r] >= h[i]:r += 1
    res = max(res , h[i] * (r - l - 1))
print(res)

第四题：有趣的数

 我们把一个数称为有趣的，当且仅当：

1. 它的数字只包含 0,1,2,3，且这四个数字都出现过至少一次。
2. 所有的 0 都出现在所有的 1 之前，而所有的 2 都出现在所有的 3 之前。
3. 最高位数字不为 0。

因此，符合我们定义的最小的有趣的数是 2013。

除此以外，4 位的有趣的数还有两个：2031 和 2301。

请计算恰好有 n 位的有趣的数的个数。

由于答案可能非常大，只需要输出答案除以 1e9+7 的余数。

输入格式

输入只有一行，包括恰好一个正整数 n。

输出格式

输出只有一行，包括恰好 n 位的整数中有趣的数的个数除以 1e9+7 的余数。

数据范围

4≤n≤1000

输入样例：

4

输出样例：

3

解题思路：我们假设先放01，再放23设01一共k位，23一共n-k位

（1）由于首位不能放0因此 01的放法一共只用 中情况

（2）由于01内部也有排法因此假设前面有 t 个 0因此01内部有（k - 1）中方法，23内部有（n-k-1）种方法

因此根据乘法原理对于每一个k都有 最终对于每一种情况求和即可

以下是代码：

c++

#include

using namespace std;

const int N = 1e3 + 10 , mod = 1e9 + 7;
int n;
int c[N][N];

int main()
{
    cin >> n;
    for(int i = 0;i <= n;i ++)
        for(int j = 0;j <= i;j ++)
            if(!j) c[i][j] = 1;
            else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
    
    int res = 0;
    for(int k = 2;k <= n - 2;k ++)
        res = (res + 1LL * c[n - 1][k] * (k - 1) % mod * (n - k - 1)) % mod;
    cout << res << endl;
    return 0;
}

Python3

import math
mod = 10 ** 9 + 7
n = int(input())
res = 0
for k in range(2 , n - 1):
    res += math.comb(n - 1 , k) * (k - 1) * (n - k - 1)
print(res % mod)

第五题：I’m stuck!

给定一个 R 行 C 列的地图，地图的每一个方格可能是 #, +, -, |, ., S, T 七个字符中的一个，分别表示如下意思：

• #: 任何时候玩家都不能移动到此方格；
• +: 当玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非 # 方格移动一格；
• -: 当玩家到达这一方格后，下一步可以向左右两个方向相邻的一个非 # 方格移动一格；
• |: 当玩家到达这一方格后，下一步可以向上下两个方向相邻的一个非 # 方格移动一格；
• .: 当玩家到达这一方格后，下一步只能向下移动一格。如果下面相邻的方格为 #，则玩家不能再移动；
• S: 玩家的初始位置，地图中只会有一个初始位置。玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非 # 方格移动一格；
• T: 玩家的目标位置，地图中只会有一个目标位置。玩家到达这一方格后，可以选择完成任务，也可以选择不完成任务继续移动。如果继续移动下一步可以向上下左右四个方向相邻的任意一个非 # 方格移动一格。

此外，玩家不能移动出地图。

请找出满足下面两个性质的方格个数：

1. 玩家可以从初始位置移动到此方格；
2. 玩家不可以从此方格移动到目标位置。

输入格式

输入的第一行包括两个整数 R 和 C，分别表示地图的行和列数。

接下来的 R 行每行都包含 C 个字符。它们表示地图的格子。地图上恰好有一个 S 和一个 T。

输出格式

如果玩家在初始位置就已经不能到达终点了，就输出 I'm stuck!。

否则的话，输出满足性质的方格的个数。

数据范围

1≤R,C≤50

输入样例：

5 5
--+-+
..|#.
..|##
S-+-T
####.

输出样例：

2

样例解释

如果把满足性质的方格在地图上用 X 标记出来的话，地图如下所示：

--+-+
..|#X
..|##
S-+-T
####X

解题思路：

（1）使用dfs进行图的遍历，进行第一个条件的判断，从S出发可以到达的点。

（2）针对每一个不是#的点，再进行一次dfs遍历，判断是否可以到达T点即可得到答案。

以下是代码：

c++

#include
#include

using namespace std;

const int N = 60;
typedef pair PII;
int dx[4] = {0 , 0 , 1 , -1} , dy[4] = {1 , -1 , 0 , 0};
bool st[N][N], st1[N][N];
string g[N];
int r , c;


void dfs(PII t)
{
    int x = t.first , y = t.second;
    
    if(x < 0 || x >= r || y < 0 || y >= c || g[x][y] == '#') return ;
    if(st[x][y]) return ;
    st[x][y] = 1;
    
    if(g[x][y] == '+' || g[x][y] == 'S' || g[x][y] == 'T') 
    {
        for(int i = 0;i < 4;i ++)
        {
            int tx = x + dx[i] , ty = y + dy[i];
            dfs({tx , ty});
        }
    }
    else if(g[x][y] == '-') dfs({x , y - 1}) , dfs({x , y + 1});
    else if(g[x][y] == '|') dfs({x + 1 , y}) , dfs({x - 1 , y});
    else if(g[x][y] == '.') dfs({x + 1 , y});
    return ;
}

int main()
{
    PII S , T;
    cin >> r >> c;
    memset(st , 0 , sizeof st);
    
    for(int i = 0;i < r;i ++)
    {
        cin >> g[i];
        for(int j = 0;j < c;j ++)
            if(g[i][j] == 'S') S = {i , j};
            else if (g[i][j] == 'T') T = {i , j};
    }
    
    dfs(S);
    
    if(!st[T.first][T.second]) 
    {
        puts("I'm stuck!");
        return 0;
    }
    
    int res = 0;
    memcpy(st1 , st , sizeof st);
    for(int i = 0;i < r;i ++)
        for(int j = 0;j < c;j ++)
        {
            memset(st , 0 , sizeof st);
            dfs({i , j});
            if(st1[i][j] && !st[T.first][T.second]) res ++;
        }
    
    cout << res << endl;
    return 0;
}