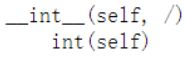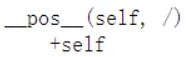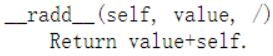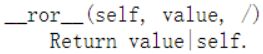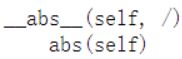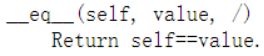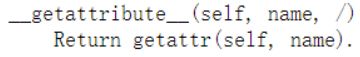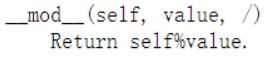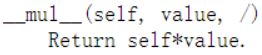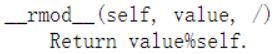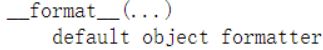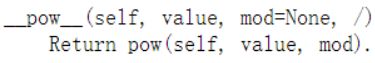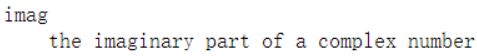Python int基本用法

• 有些功能在专栏文章python str基本用法中已经写过了，在这里就简略写个例子

目录

1  没什么用的

1.1  向上取整 __ceil__()

1.2  向下取整 __floor__()

1.3  如果变量适合作为列表的索引则返回自身，否则报错 __index__()

1.4  返回整形 __int__()

1.5  实例化后在__init__()前调用

1.6  在自身前面加一个正号 __pos__()

1.7  反向相加 __radd__()

1.8  反向相乘 __rmul__()

1.9  反向按位或运算 __ror__()

1.10  返回整数部分 __trunc__()

2  不常用的¶

2.1  相加 __add__()

​2.2  逻辑‘和’运算 __and__()

2.3  返回布尔量 __bool__()

2.4  返回一个元组，第一个元素为除数，第二个元素为余数 __divmod__()

2.5  返回绝对值 __abs__()

2.6  判断是否相等 __eq__()

2.7  将变量转换为浮点型 __float__()

2.8  返回商 __floordiv__()

2.9  大于等于 __ge__()

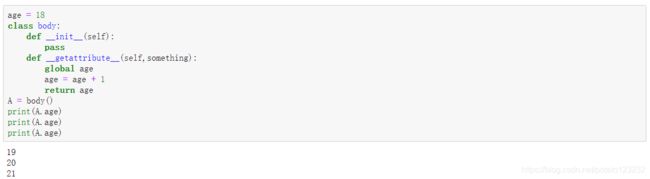
2.10  调用属性时自动执行 __getattribute__()

2.11  大于 __gt__()

2.12  返回哈希值 __hash__()

2.13  小于等于 __le__()

2.14  大于 __lt__()

2.15  返回余数 __mod__()

2.16  返回乘积 __mul__()

2.17  不等于 __ne__()

2.18  相反数 __neg__()

2.19  将变量转换为字符串 __repr__()

2.20  反向返回除法元组 __rdivmod__()

2.21  反向返回商 __rfloordiv__()

2.22  反向 转变为2进制，在末尾(右侧)补指定个零 __rlshift__()

2.23  反向取余 __rmod__()

2.24  五舍六入 __round__()

2.25  反向先幂运算再取余 __rpow__()

2.26  反向二进制后前方(左侧)补零,后面删除 __rrshift__()

2.27  二进制后前方(左侧)补零,后面删除 __rshift__()

2.28  反向相减 __rsub__()

2.29  将变量转换为字符串 __str__()

2.30  变量相减 __sub__()

2.31  变量相除 __truediv__()

3  常用的

3.1  创建整形 int

3.2  格式转换 __format__()

3.3  将变量转变为元组，第一个元素为指定的变量 __getnewargs__()

3.4  以0为中点，取该变量的对应点 __invert__()

3.5  在二进制状态下，在末尾（右侧）补指定个0 __lshift__()

3.6  按位或运算 __or__()

3.7  先幂运算，再取余 __pow__()

3.8  反向相除 __rtruediv__()

3.9  反向异或运算 __xor__()

3.10  返回变量字节大小 __sizeof__()

3.11  异或运算 __xor__()

3.12  二进制下能表达该变量的最小位数 bit_length()

3.13  返回共轭复数 conjuate()

3.14  字节数组转换为十进制数组 from_btyes()

3.15  将十进制数转换为字节类型 to_bytes()

4  help(int)最后还有4个定义分别为

4.1  分母

4.2  虚部

4.3  分子

4.4  实部

---

1  没什么用的

1.1  向上取整 __ceil__()

1.2  向下取整 __floor__()

 由于本身是整形，所以返回自身

1.3  如果变量适合作为列表的索引则返回自身，否则报错 __index__()

1.4  返回整形 __int__()

1.5  实例化后在__init__()前调用

1.6  在自身前面加一个正号 __pos__()

如果是负值的时候是不会在前面加一个+字符的

1.7  反向相加 __radd__()

1.8  反向相乘 __rmul__()

1.9  反向按位或运算 __ror__()

他的运算方式是这样的，1为0001，4为0100。每一位相同取0，不相同取1，最后结果为0101，0101为5

1.10  返回整数部分 __trunc__()

2  不常用的¶

2.1  相加 __add__()

2.2  逻辑‘和’运算 __and__()

可用and替代

2.3  返回布尔量 __bool__()

可用bool替代

2.4  返回一个元组，第一个元素为除数，第二个元素为余数 __divmod__()

可用divmod替代

2.5  返回绝对值 __abs__()

可用abs替代

2.6  判断是否相等 __eq__()

可以用 == 替代

2.7  将变量转换为浮点型 __float__()

可以用float替代

2.8  返回商 __floordiv__()

可以用 // 替代

2.9  大于等于 __ge__()

可以用 >= 替代

2.10  调用属性时自动执行 __getattribute__()

2.11  大于 __gt__()

2.12  返回哈希值 __hash__()

可以用hash替代

2.13  小于等于 __le__()

2.14  大于 __lt__()

2.15  返回余数 __mod__()

可以用%号替代

2.16  返回乘积 __mul__()

2.17  不等于 __ne__()

2.18  相反数 __neg__()

2.19  将变量转换为字符串 __repr__()

2.20  反向返回除法元组 __rdivmod__()

13 / 5 商2余3

2.21  反向返回商 __rfloordiv__()

2.22  反向 转变为2进制，在末尾(右侧)补指定个零 __rlshift__()

4为0100，位数向左移动一位

0100 -> 1000

2.23  反向取余 __rmod__()

2.24  五舍六入 __round__()

如果是整形会返回自身

2.25  反向先幂运算再取余 __rpow__()

直接幂运算

先幂运算再取余

2.26  反向二进制后前方(左侧)补零,后面删除 __rrshift__()

由于help文档顺序的原因，我们先介绍__rrshift__(),后介绍__rshift__()

现在介绍的这个是反向，一会儿介绍的是正向

0101 -> 0010

2.27  二进制后前方(左侧)补零,后面删除 __rshift__()

0100 -> 0001

2.28  反向相减 __rsub__()

2.29  将变量转换为字符串 __str__()

2.30  变量相减 __sub__()

2.31  变量相除 __truediv__()

3  常用的

3.1  创建整形 int

int中有一个参数base，默认是10(十进制)，可以改成2-36进制

或者当base为0时可转换二进制字符

3.2  格式转换 __format__()

我们看一下以ascii中所有值为参数的结果

__format__()的返回值类型都为str

0-9 < > ^ 之前在字符串内介绍过

空格我们可以明显看出来是在变量前面加一个空格

% 是变成浮点百分号形式，+是在前面加个+，E,e是科学计数法，F,f是浮点数，X,x是16进制，b是二进制，o是八进制

剩下的我们就不太能一眼看出来了

我们现在更改变量

这次我们可以看出

，_ 为分隔符

G和g当数字小时普通表示，数字大时科学计数法表示

我们还有 n,#,-,=是我们不知道的

我上网查了一下

- 号是如果值为负值，显示负号

n 是如果为整数和d相同，如果为浮点和g相同，简单来讲是返回本身

#和=测试了一下可以凑齐位数

现在我们就把参数都理清了，我们总结一下

我们可以把格式转换分以下类

• 字符位数转换
  • 空格 在指定变量前加空格
  • 0-9 将变量搞成指定的位数，如果如果字符比位数多
  • < 左对齐
  • > 右对齐
  • ^ 中间对齐
  • = 凑齐位数
  • # 凑齐位数
• 字符格式转换
  • % 将变量转变为浮点%形式
  • + 在变量前面加一个+号
  • - 如果值是赋值在前方加一个-号
  • E 科学计数法形式
  • F 浮点数形式
  • G 普通形式，数量过大时会用科学计数法表示
  • c 转换为Unicode字符
  • e 同E，科学计数法
  • f 同f，浮点数形式
  • g 同G，普通形式
  • n 数字。当值为整数时和'd'相同，值为浮点数时和'g'相同。不同的是它会根据区域设置插入数字分隔符。
  • _ 分隔符
  • ，分隔符
• 进制转换
  • X 十六进制
  • b 二进制
  • d 十进制
  • o 八进制
  • x 同X，十六进制

3.3  将变量转变为元组，第一个元素为指定的变量 __getnewargs__()

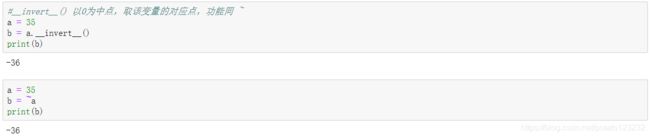
3.4  以0为中点，取该变量的对应点 __invert__()

• 注：与相反数还是有区别的

3.5  在二进制状态下，在末尾（右侧）补指定个0 __lshift__()

0001 - > 0100

3.6  按位或运算 __or__()

• 注：和or不一样，or是通过True或False运算的，两个正数返回第一个结果

3.7  先幂运算，再取余 __pow__()

当然我们可以直接平方

__pow__()也是可以替代的

3.8  反向相除 __rtruediv__()

3.9  反向异或运算 __xor__()

• 异或：相同为False，不同为True

两个值都为数值时按位异或，咱们以4和2举例

3.10  返回变量字节大小 __sizeof__()

3.11  异或运算 __xor__()

• 异或：相同为False，不同为True

两个值都为数值时按位异或，咱们以4和2举例

3.12  二进制下能表达该变量的最小位数 bit_length()

8对应1000

3.13  返回共轭复数 conjuate()

如果没有虚部则返回自身

有虚部则返回共轭复数

3.14  字节数组转换为十进制数组 from_btyes()

#from_bytes功能为将字节数组转换为十进制int
#必选参数为bytes(字节数组内容)，byteorder(字节顺序)
#byteorder参数分为little与big
#little 逆字符数组顺序，例中为 f1 f0 即为 1111 0001 1111 0000
b = int.from_bytes(b'\xf0\xf1', byteorder = 'little')
print(b)
#big 字符数组正常顺序 ，例中为 f0 f1 即为1111 0000 1111 0001
b = int.from_bytes(b'\xf0\xf1', byteorder = 'big')
print(b)

#可选参数为signed，若signed 为 True，则对结果依次进行原码，反码，补码的操作
#signed函数为关键字参数
b = int.from_bytes(b'\xf0\xf1', byteorder = 'big',signed = True)
print(b)
#以下为例中signed为True的运算方法,最高位在转换中既当做单位，也当做数值，照常参与运算，0为正号，1为负号
#原码（不变）
#1 111 0000 1111 0001
#反码（相反）
#0 000 1111 0000 1110
#补码 （在字节数组的最后+1）
#0 000 1111 0000 1111

我们现在再举一个逆序的例子

原码

1 111 0001 1111 0000

反码

0 000 1110 0000 1111

补码

0 000 1110 0001 0000

所以此次signed = True的结果应为 -3600

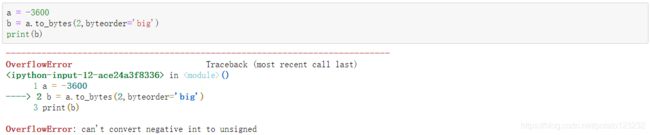
3.15  将十进制数转换为字节类型 to_bytes()

二进制数为 1111 0001 1111 0000 转换后为61936

二进制数为 0000 1110 0001 0000 转换后为3600

但是我们不能转变负值

4  help(int)最后还有4个定义分别为

4.1  分母

有理数的最小分母

4.2  虚部

虚数的虚部

4.3  分子

有理数的最小分子

4.4  实部

虚数的实部