【深度学习 | 计算机视觉】Focal Loss原理及其实践（含源代码）

参考文献：

https://www.jianshu.com/p/437ce8ed0413

一、导读

Focal Loss 是一个在交叉熵（CE）基础上改进的损失函数，来自ICCV2017的Best student paper—Focal Loss for Dense Object Detection。

Focal Loss的提出源自图像领域中目标检测任务中样本数量不平衡的问题，并且这里所谓的不平衡性跟平常理解的是有所区别的，它还强调样本的难易性。尽管Focal Loss始于目标检测场景，其实它可以应用到很多其他任务场景，只要符合它的问题背景，就可以试试，就有意想不到的效果。

二、Focal Loss 原理

在引入Focal Loss公式前，我们以源paper中目标检测的任务来说：目标检测器通常会产生高达100k的候选目标，只有极少数是正样本，正负样本数量非常不平衡。

在计算分类的时候常用的损失—交叉熵（CE）的公式如下：
$$CE(p,y)=\{\begin{array}{rcl}-\log (p)& & ify=1\\ -\log (1-p)& & otherwise\end{array}$$

其中$y$取值{1，-1}，代表正负样本，$p$为模型预测的label概率，通常$p>0.5$就判断为正样本，否则为负样本。论文中为了方便展示，重新定义了$p_t$：
$$p_t=\{\begin{array}{rcl}p& & ify=1\\ 1-p& & otherwise\end{array}$$
这样CE函数就可以表示为：$CE(p,y)=CE(p_t)=-\log (p_t)$

在CE的基础上，为了解决正负样本不平衡性，有人提出一种带权重的CE函数：
$$CE(p_t)=-{\alpha }_t\log (p_t)$$
其中当：$y=1,{\alpha }_t=\alpha ;y=-1,{\alpha }_t=1-\alpha$，参数$\alpha$为控制正负样本的权重，取值范围为[0, 1]。

尽管这是一种很简单的解决正负样本不平衡的方案，但它还没有真正达到paper中作者想解决的问题：因为正负样本中也有难易之分，认为模型应该更聚焦在难样本的学习上。如下图，按正负，难易，可将样本分为四个维度，其实上面带权重的CE函数，只是解决了正负问题，并没有解决难易问题。

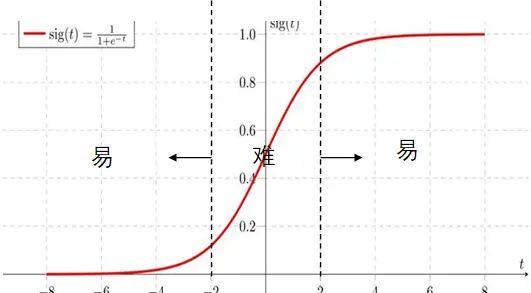
那么怎么来衡量一个样本的难易程度，更何况真实数据也没有这个标记。其实，这里的样本难易是用模型来判断的，就正样本集合来说，如果一个样本预测的$p=0.9$，一个样本预测的$p=0.6$，明显前一个样本更容易学习，或者说特征更明显，是易样本。这样也就是说，预测的概率越接近于1或者0的样本，就越是容易学习的样本，相反，越是集中于0.5左右的样本，就是难样本。在sigmoid函数上，可以按下图的方式展示样本的难易之分。

怎么让模型对难易样本也有区分性的学习，也是说聚焦程度不同。模型应该花更多精力在难样本的学习上，而减少精力在易样本的学习，之前的CE函数，以及带权重的CE函数，都是将难样本、易样本等同看待的。这样就引出Focal Loss的表达形式：
$$FL(p_t)=-(1-p_t{)}^{\gamma }\log (p_t)$$
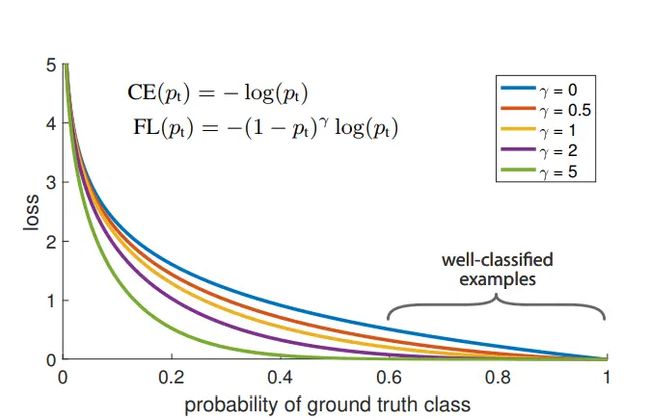
其中$\gamma$为调节因子，取值为[0, 5]，当$\gamma =0$，就等同于CE函数；$\gamma$值越大，表示模型在难易样本上聚焦的更厉害。下图是不同参数下表现形式：

结合上图与公式，可以看出，当$p_t$趋近于1时，权重$(1-p_t{)}^{\gamma }$趋近于0，对总损失贡献几乎没有影响，意味着模型较少对这类样本的学习；比如，在正样本集合中，$\gamma =2$，当一样本$p_t=0.6$，当一样本$p_t=0.7$，二者相对来说，前者是难样本，后者是易样本，反映在Focal Loss上，前者的对总损失贡献权重为0.16，后者0.09，明显难样本贡献权重更大，模型也就会更将聚焦对其学习。同理，负样本中一样。

但是上面的Focal Loss公式只是体现了难易样本的区分，没有区分正负。这样就引出了完整版的Focal Loss表达形式：
$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$
这样Focal Loss既能调整正负样本的权重，又能控制难易分类样本的权重。paper中通过实验验证，默认$\gamma =2$，${\alpha }_t=0.25(y=1)$。在这里${\alpha }_t$取值上可能会有疑问，理论上正样本权重更大些，取0.75，而paper实验结果给的是0.25。

自己的理解：主要原因是$\gamma =2$，而大部分负样本的$p<0.1$，导致负样本的贡献权重还小于正样本贡献的权重，本意是想调高正样本的贡献权重，但这样就有点调的过大了，所以${\alpha }_t=0.25(y=1)$就有点反过来提高下负样本的权重。所以在最终版中，不能理解${\alpha }_t$就是完全来调节正负样本的权重的，而是要结合${\alpha }_t(1-p_t{)}^{\gamma }$一起来看。

三、实验对比

使用标准的二进制交叉熵损失函数和Focal Loss函数分别训练同一个模型的过程,主要分为以下几步：

1. 加载MNIST数据集,仅保留数字2的样本作为正样本,其他作为负样本。
2. 定义Focal Loss损失函数。其中alpha和gamma是超参数。
3. 构建简单的全连接网络模型。
4. 首先用二进制交叉熵损失函数编译模型,并训练。
5. 然后用定义的Focal Loss函数编译模型,其他保持不变,并训练。
6. 这样可以在同一个模型上分别观察不同损失函数的训练效果。

Focal Loss的目的是降低易分类样本的loss值,让模型更集中优化硬分类样本。

所以这段代码通过直接比较,演示了不同损失函数对模型训练效果的影响,是一个很好的实验示例。

通过输出的训练过程和结果,可以直观分析Focal Loss相比于标准交叉熵在这一任务上的效果。

3.1 使用交叉熵损失函数

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import numpy as np
import tensorflow.keras.backend as K

# load dataset
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.reshape(60000, 784).astype('float32') / 255
X_test = X_test.reshape(10000, 784).astype('float32') / 255

y_train = np.array([1 if d == 2 else 0 for d in y_train])
y_test = np.array([1 if d == 2 else 0 for d in y_test])
#定义focal loss
def focal_loss(gamma = 2., alpha = .25):
    def focal_loss_fixed(y_true, y_pred):
        pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
        pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
        return -K.sum(alpha * K.pow(1. - pt_1, gamma) * K.log(K.epsilon() + pt_1))\
            - K.sum((1 - alpha) * K.pow( pt_0, gamma) * K.log(1. - pt_0 + K.epsilon()))
    return focal_loss_fixed

#build model
inputs = keras.Input(shape = (784,), name = 'mnist_input')
h1 = layers.Dense(64, activation = 'relu')(inputs)
outputs = layers.Dense(1, activation = 'sigmoid')(h1)
model = tf.keras.Model(inputs, outputs)

#以平方差损失函数来编译模型进行训练
model.compile(optimizer = keras.optimizers.RMSprop(),
             loss = keras.losses.BinaryCrossentropy(),
             metrics = ['accuracy'])

#training
history = model.fit(X_train, y_train, batch_size = 64, epochs = 10,
         validation_data = (X_test, y_test))

我们的训练过程为：

Epoch 1/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0604 - accuracy: 0.9821 - val_loss: 0.0331 - val_accuracy: 0.9907
Epoch 2/10
938/938 [==============================] - 1s 997us/step - loss: 0.0274 - accuracy: 0.9916 - val_loss: 0.0241 - val_accuracy: 0.9935
Epoch 3/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0203 - accuracy: 0.9940 - val_loss: 0.0225 - val_accuracy: 0.9937
Epoch 4/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0163 - accuracy: 0.9948 - val_loss: 0.0208 - val_accuracy: 0.9942
Epoch 5/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0137 - accuracy: 0.9958 - val_loss: 0.0181 - val_accuracy: 0.9949
Epoch 6/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0114 - accuracy: 0.9967 - val_loss: 0.0168 - val_accuracy: 0.9949
Epoch 7/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0099 - accuracy: 0.9973 - val_loss: 0.0192 - val_accuracy: 0.9942
Epoch 8/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0085 - accuracy: 0.9974 - val_loss: 0.0180 - val_accuracy: 0.9945
Epoch 9/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0074 - accuracy: 0.9981 - val_loss: 0.0180 - val_accuracy: 0.9942
Epoch 10/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0061 - accuracy: 0.9982 - val_loss: 0.0150 - val_accuracy: 0.9954

3.2 使用Focal Loss 损失函数

import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
import numpy as np
import tensorflow.keras.backend as K

# load dataset
(X_train, y_train), (X_test, y_test) = tf.keras.datasets.mnist.load_data()
X_train = X_train.reshape(60000, 784).astype('float32') / 255
X_test = X_test.reshape(10000, 784).astype('float32') / 255

y_train = np.array([1 if d == 2 else 0 for d in y_train])
y_test = np.array([1 if d == 2 else 0 for d in y_test])
#定义focal loss
def focal_loss(gamma = 2., alpha = .25):
    def focal_loss_fixed(y_true, y_pred):
        pt_1 = tf.where(tf.equal(y_true, 1), y_pred, tf.ones_like(y_pred))
        pt_0 = tf.where(tf.equal(y_true, 0), y_pred, tf.zeros_like(y_pred))
        return -K.sum(alpha * K.pow(1. - pt_1, gamma) * K.log(K.epsilon() + pt_1))\
            - K.sum((1 - alpha) * K.pow( pt_0, gamma) * K.log(1. - pt_0 + K.epsilon()))
    return focal_loss_fixed

#build model
inputs = keras.Input(shape = (784,), name = 'mnist_input')
h1 = layers.Dense(64, activation = 'relu')(inputs)
outputs = layers.Dense(1, activation = 'sigmoid')(h1)
model = tf.keras.Model(inputs, outputs)

#以Focal Loss损失函数来编译模型进行训练
model.compile(optimizer = keras.optimizers.RMSprop(),
             loss = [focal_loss(alpha = .25, gamma = 2)],
             metrics = ['accuracy'])

#training
history = model.fit(X_train, y_train, batch_size = 64, epochs = 10,
         validation_data = (X_test, y_test))

我们的训练过程为：

Epoch 1/10
938/938 [==============================] - 1s 1ms/step - loss: 0.3401 - accuracy: 0.9829 - val_loss: 0.2087 - val_accuracy: 0.9884
Epoch 2/10
938/938 [==============================] - 1s 1ms/step - loss: 0.1733 - accuracy: 0.9920 - val_loss: 0.1711 - val_accuracy: 0.9925
Epoch 3/10
938/938 [==============================] - 1s 1ms/step - loss: 0.1355 - accuracy: 0.9942 - val_loss: 0.1642 - val_accuracy: 0.9941
Epoch 4/10
938/938 [==============================] - 1s 1ms/step - loss: 0.1128 - accuracy: 0.9952 - val_loss: 0.1766 - val_accuracy: 0.9904
Epoch 5/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0967 - accuracy: 0.9959 - val_loss: 0.1334 - val_accuracy: 0.9948
Epoch 6/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0827 - accuracy: 0.9968 - val_loss: 0.1906 - val_accuracy: 0.9952
Epoch 7/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0738 - accuracy: 0.9970 - val_loss: 0.1455 - val_accuracy: 0.9949
Epoch 8/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0652 - accuracy: 0.9975 - val_loss: 0.1504 - val_accuracy: 0.9946
Epoch 9/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0562 - accuracy: 0.9979 - val_loss: 0.1327 - val_accuracy: 0.9943
Epoch 10/10
938/938 [==============================] - 1s 1ms/step - loss: 0.0514 - accuracy: 0.9980 - val_loss: 0.1649 - val_accuracy: 0.9943

3.3 总结

从结果可以看出，虽然在该数据集上二者提升效果并不大，但Focal Loss在每轮上都优于CE的训练效果，所以还是能体现Focal Loss的优势，如果在其他更不平衡的数据集上，应该效果更好。

不管在CV，还是NLP领域，该损失函数值得大家去尝试。