【布局优化】基于人工蜂群算法的无线传感器网(WSN)覆盖优化matlab源码
一、WSN模型
1.1 动机
近年来,随着对等网络、云计算和网格计算等分布式环境的发展,无线传感器网络(WSN)得到了广泛的应用。无线传感器网络(WSN)是一种新兴的计算和网络模式,它可以被定义为一个由称为传感器节点的微小、小型、昂贵和高度智能化的设备组成的网络。传感器节点位于被观测空间内的不同位置,通过无线通信信道交换从监测领域收集的数据。收集的数据被发送到sink节点,sink节点要么本地处理数据,要么将数据发送到处理能力更强的其他网络。
无线传感器网络最基本的挑战之一是节点定位。节点定位问题的实例很多,属于NP难优化问题。传统的确定性技术和算法不能在合理的计算时间内解决NP-hard问题。在这种情况下,最好采用非确定性(随机)算法,如元启发式算法。
群体智能元启发式算法模拟自然界中的生物群体,如鸟和鱼的群体、蜜蜂和蚂蚁的群体、蝙蝠和杜鹃鸟的群体等。这些算法是基于种群的、随机的和迭代的搜索方法,基于四个自组织原则:正反馈、负反馈,多重相互作用和波动。
1.2 无线传感器网络中的定位问题
定位问题是无线传感器网络中研究最多的问题之一,因为如果传感器节点的位置未知,则覆盖、功率和路由都将无法确定最佳。定位是无线传感器网络的关键。一些传感器节点的位置可以由全球定位系统(GPS)来定义,这些节点被称为锚节点或信标节点,而其他传感器节点则随机分布在搜索空间中。这些节点称为未知节点或传感器节点。由于每个节点的电池寿命、成本、气候条件等因素,只有少数节点的位置是由GPS坐标确定的,而其他节点的位置则需要采用定位算法进行估计。
针对无线传感器网络中传感器节点的定位问题,提出了锚节点和未知节点两种定位算法。第一阶段称为测距阶段,算法确定未知节点和相邻锚节点之间的距离。针对无线传感器网络中传感器节点的定位问题,提出了锚节点和未知节点两种定位算法。第一阶段称为测距阶段,算法确定未知节点和相邻锚节点之间的距离。第二阶段通过在第一阶段使用各种方法收集测距信息来估计节点的位置,如到达角(AOA)、到达时间(TOA)、到达时差(TDOA)、往返时间(RTT)、无线信号强度(RSS)等。
1.3 问题陈述
在由M个传感器节点组成的无线传感器网络中,定位问题的目标是利用M-N个锚节点的位置信息,在传输范围为R的情况下,估计N个未知节点的位置,如果一个传感器节点在三个或更多锚节点的传输范围内,则认为它是定位的。这是一个总坐标数为2n的二维定位问题。
本文采用RSS方法估计节点间距离。无论采用何种测距方法,都可能出现不精确的测量。N个未知节点坐标的位置估计可以表示为一个优化问题,涉及表示节点定位误差的目标函数的最小化[19]。该问题的目标函数由N个未知节点和M N个相邻锚节点之间的误差平方和表示[19]。
随着RSS的出现,三边测量将被用来解决WSN中的定位问题。该方法的原理是基于三个锚节点的已知位置。未知节点的位置可以在三个锚节点的传输范围内估计。
每个节点估计到第i个锚点的距离为d̂=di+ni,其中ni是高斯噪声,di是使用以下等式计算的实际距离:
应最小化的目标函数表示为计算节点坐标的实际和估计距离与实际节点坐标之间的均方误差(MSE):
其中di是实际距离,d̂i是估计距离(从噪声范围测量获得的值di),M≥3(传感器节点的位置在传输范围R内至少需要三个锚)。
由于节点定位中的距离测量是有噪声的,为了估计节点之间的足够距离,采用了群体智能元启发式等优化方法。
二、人工蜂群算法
受到蜜蜂群体的有组织的觅食过程的启发,Karaboga提出了模拟蜜蜂群体觅食过程的人工蜂群(Artificial Bee Colony) 算法用于解决多维度多峰谷的优化问题。该算法创始之初被用来寻找Sphere、Rosenbrock和Rastrigin函数的最小值。 首先对蜜蜂基于摇摆舞进行觅食的过程特征进行介绍。在图1中,存在两个已发现的食物源A和B。初始时,潜在工蜂以非雇佣蜂的身份进行搜索。它并不知道蜂房附近的任何蜜源的信息。因此,它有以下两个可能的选择: (1)成为一个侦察蜂,秉着自身潜在动力或外在因素自发的搜索蜂房附近的区域(见图1中的S); (2)在观看摆尾舞后,成为一个被招募者,并开始搜索蜜源(见图1中的R)。 在定位蜜源之后,该蜜蜂能够利用自身的能力来记住食物源的位置,并立刻对它进行探索。该蜜蜂现在成为了一个雇佣蜂。雇佣蜂采到蜂蜜后,从蜜源处返回蜂房并将蜂蜜卸载到蜜室中。在卸载完蜂蜜后,雇佣蜂有下列三个选择: (1)放弃已经采集过的蜜源,成为一个受其他摇尾舞招募的跟随者(UF)。 (2)施展摇尾舞技,招募蜂房内的同伴,再次回到原先采集过的食物源(EF1)。 (3)不招募其它的蜜蜂,继续探索采集过的食物源(EF2)。 
图1 蜜蜂觅食行为图
算法流程
人工蜂群算法由连续的四个阶段组成,分别是初始化阶段、引领(雇佣)蜂阶段、跟随蜂阶端和侦察蜂阶段。 人工蜂群算法中将人工蜂群分为引领蜂、跟随蜂和侦察蜂三类,每一次搜索过程中,引领蜂和跟随蜂是先后开采食物源,即寻找最优解,而侦察蜂是观察是否陷入局部最优,若陷入局部最优则随机地搜索其它可能的食物源。每个食物源代表问题一个可能解,食物源的花蜜量对应相应解的质量(适应度值f i t fitfit)。 ABC算法流程图如图2所示。 
图2 ABC算法流程图
1、初始化阶段
2、引领蜂阶段
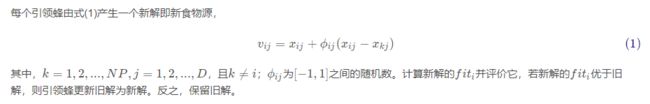
 3、跟随蜂阶段
3、跟随蜂阶段
4、侦察蜂阶段
5、食物源
三、代码
CostFunction=@(x) Sphere(x); % Cost Function
nVar=5; % Number of Decision Variables
VarSize=[1 nVar]; % Decision Variables Matrix Size
VarMin=-10; % Decision Variables Lower Bound
VarMax= 10; % Decision Variables Upper Bound
%% ABC Settings
MaxIt=200; % Maximum Number of Iterations
nPop=100; % Population Size (Colony Size)
nOnlooker=nPop; % Number of Onlooker Bees
L=round(0.6*nVar*nPop); % Abandonment Limit Parameter (Trial Limit)
a=1; % Acceleration Coefficient Upper Bound
%% Initialization
% Empty Bee Structure
empty_bee.Position=[];
empty_bee.Cost=[];
% Initialize Population Array
pop=repmat(empty_bee,nPop,1);
% Initialize Best Solution Ever Found
BestSol.Cost=inf;
% Create Initial Population
for i=1:nPop
pop(i).Position=unifrnd(VarMin,VarMax,VarSize);
pop(i).Cost=CostFunction(pop(i).Position);
if pop(i).Cost<=BestSol.Cost
BestSol=pop(i);
end
end
% Abandonment Counter
C=zeros(nPop,1);
% Array to Hold Best Cost Values
BestCost=zeros(MaxIt,1);
%% ABC Main Loop
for it=1:MaxIt
% Recruited Bees
for i=1:nPop
% Choose k randomly, not equal to i
K=[1:i-1 i+1:nPop];
k=K(randi([1 numel(K)]));
% Define Acceleration Coeff.
phi=a*unifrnd(-1,+1,VarSize);
% New Bee Position
newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
% Evaluation
newbee.Cost=CostFunction(newbee.Position);
% Comparision
if newbee.Cost<=pop(i).Cost
pop(i)=newbee;
else
C(i)=C(i)+1;
end
end
% Calculate Fitness Values and Selection Probabilities
F=zeros(nPop,1);
MeanCost = mean([pop.Cost]);
for i=1:nPop
F(i) = exp(-pop(i).Cost/MeanCost); % Convert Cost to Fitness
end
P=F/sum(F);
% Onlooker Bees
for m=1:nOnlooker
% Select Source Site
i=RouletteWheelSelection(P);
% Choose k randomly, not equal to i
K=[1:i-1 i+1:nPop];
k=K(randi([1 numel(K)]));
% Define Acceleration Coeff.
phi=a*unifrnd(-1,+1,VarSize);
% New Bee Position
newbee.Position=pop(i).Position+phi.*(pop(i).Position-pop(k).Position);
% Evaluation
newbee.Cost=CostFunction(newbee.Position);
% Comparision
if newbee.Cost<=pop(i).Cost
pop(i)=newbee;
else
C(i)=C(i)+1;
end
end
% Scout Bees
for i=1:nPop
if C(i)>=L
pop(i).Position=unifrnd(VarMin,VarMax,VarSize);
pop(i).Cost=CostFunction(pop(i).Position);
C(i)=0;
end
end
% Update Best Solution Ever Found
for i=1:nPop
if pop(i).Cost<=BestSol.Cost
BestSol=pop(i);
end
end
% Store Best Cost Ever Found
BestCost(it)=BestSol.Cost;
% Display Iteration Information
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it))]);
end
%% Results
figure;
%plot(BestCost,'LineWidth',2);
semilogy(BestCost,'LineWidth',2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;
四、参考文献





