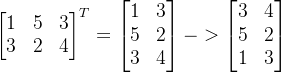第四次CCF计算机软件能力认证
第一题:图像旋转
旋转是图像处理的基本操作,在这个问题中,你需要将一个图像逆时针旋转 90 度。
计算机中的图像表示可以用一个矩阵来表示,为了旋转一个图像,只需要将对应的矩阵旋转即可。
输入格式
输入的第一行包含两个整数 n,m,分别表示图像矩阵的行数和列数。
接下来 n 行每行包含 m 个整数,表示输入的图像。
输出格式
输出 m 行,每行包含 n 个整数,表示原始矩阵逆时针旋转 90 度后的矩阵。
数据范围
1≤n,m≤1,000,
矩阵中的数都是不超过 1000 的非负整数。输入样例:
2 3 1 5 3 3 2 4输出样例:
3 4 5 2 1 3
解题思路:就是矩阵转置之后倒序输出就行
以下是代码:
c++
#include
using namespace std;
const int N = 1010;
int g[N][N] , n , m;
void solve()
{
for(int i = m - 1;i >= 0;i --)
{
for(int j = 0;j < n;j ++)
cout << g[j][i] << " ";
cout << endl;
}
}
int main()
{
cin >> n >> m;
for(int i = 0;i < n;i ++)
for(int j = 0;j < m;j ++)
cin >> g[i][j];
solve();
return 0;
} Python
n , m = map(int , input().split())
matrix = []
for i in range(n):
matrix.append(list(map(int , input().split())))
for i in range(m - 1 , -1 , -1):
for j in range(n):
print(matrix[j][i] , end = ' ')
print()第二题:数字排序
给定 n 个整数,请统计出每个整数出现的次数,按出现次数从多到少的顺序输出。
输入格式
输入的第一行包含一个整数 n,表示给定数字的个数。
第二行包含 n 个整数,相邻的整数之间用一个空格分隔,表示所给定的整数。
输出格式
输出多行,每行包含两个整数,分别表示一个给定的整数和它出现的次数。
按出现次数递减的顺序输出。如果两个整数出现的次数一样多,则先输出值较小的,然后输出值较大的。
数据范围
1≤n≤1000,
给出的数都是不超过 1000 的非负整数。输入样例:
12 5 2 3 3 1 3 4 2 5 2 3 5输出样例:
3 4 2 3 5 3 1 1 4 1
解题思路:遍历一遍统计每一个数的出现次数,根据这个规则按出现次数递减的顺序输出,如果两个整数出现的次数一样多,则先输出值较小的,然后输出值较大的。
以下是代码:
c++
#include
#include
#include
using namespace std;
const int N = 1010;
typedef pair PII;
int a[N];
int n, idx = 0;
PII b[N];
bool cmp(PII a , PII b)
{
if(a.first != b.first) return a.first > b.first;
return a.second < b.second;
}
int main()
{
memset(a , 0 , sizeof a);
cin >> n;
for(int i = 0;i < n;i ++)
{
int x;
cin >> x;
a[x] ++;
}
for(int i = 0;i <= 1000;i ++)
if(a[i]) b[idx ++] = {a[i] , i};
sort(b , b + idx , cmp);
for(int i = 0;i < idx;i ++)
cout << b[i].second << " " << b[i].first << endl;
return 0;
} Python
# Python真的好慢
from collections import Counter
n = int(input())
d = Counter(list(map(int , input().split())))
l = [[i , j] for i , j in d.items()]
res = sorted(l , key = lambda x : (x[1] * -1 , x[0]))
for i in res:
print(i[0] , i[1])第三题:节日
有一类节日的日期并不是固定的,而是以“a 月的第 b 个星期 c”的形式定下来的,比如说母亲节就定为每年的五月的第二个星期日。
现在,给你 a,b,c 和 y1,y2,希望你输出从公元 y1 年到公元 y2 年间的每年的 a 月的第 b 个星期 c 的日期。
提示:关于闰年的规则:年份是 400 的整数倍时是闰年,否则年份是 4 的倍数并且不是 100 的倍数时是闰年,其他年份都不是闰年。
例如 1900 年就不是闰年,而 2000 年是闰年。
为了方便你推算,已知 1850 年 1 月 1 日是星期二。
输入格式
输入包含恰好一行,有五个整数 a,b,c,y1,y2。
其中 c=1,2,……,6,7 分别表示星期一、二、……、六、日。
输出格式
对于 y1 和 y2 之间的每一个年份,包括 y1 和 y2,按照年份从小到大的顺序输出一行。
如果该年的 a 月第 b 个星期 c 确实存在,则以
yyyy/mm/dd的格式输出,即输出四位数的年份,两位数的月份,两位数的日期,中间用斜杠/分隔,位数不足时前补零。如果该年的 a 月第 b 个星期 c 并不存在,则输出
none。数据范围
1≤a≤12,
1≤b≤5,
1≤c≤7,
1850≤y1,y2≤2050输入样例:
5 2 7 2014 2015输出样例:
2014/05/11 2015/05/10
解题思路:枚举从1850年一直枚举到y2年,对于每一天求出每一天的对应的信息,至于是否输出即要判断年份是否合法,月日星期是否符合要求。
几个特别的函数,判断是否是闰年,求每一个月有多少天。
以下是代码:
c++
#include
#include
#include
using namespace std;
//日期题套路,12个月,开13个位置,第0个为占位符
int months[13] = {
0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31
};
//判断某一年是否是闰年的函数
int is_leap(int year)
{
if(year % 400 == 0 || (year % 4 == 0 && year % 100)) return 1;
return 0;
}
//求某月有多少天的函数
int get_days(int year, int month)
{
if(month == 2) return months[month] + is_leap(year); //如果是2月的话返回天数和是否是闰年,如果是闰年2月份+1天
return months[month]; //不是2月份则直接返回天数即可
}
//星期一到星期日用0~6表示
int main()
{
int a, b, c, y1, y2;
cin >> a >> b >> c >> y1 >> y2;
int days = 0; //表示过了多少天
for(int year = 1850; year <= y2; year ++ )
for(int month = 1; month <= 12; month ++ )
{
if(year >= y1 && month == a)
{
int w = (1 + days) % 7; //先算一下这个月的1月1号是星期几,1850年1月1日是星期二,下标为1
int cnt = 0; //统计一下当前是枚举到的第几个星期c
for(int d = 1; d <= get_days(year, month); d ++ ) //枚举一下这个月的所有天
{
if(w == c - 1) //星期的下标从0开始,所以要-1,如星期七的下标是6
cnt ++ ;//星期c的个数++
if(cnt == b) //如果星期c的个数等于b的话,满足条件,输出
{
printf("%04d/%02d/%02d\n", year, month, d);
break;
}
w = (w + 1) % 7; //每过一天,星期需要往后错一位
}
if(cnt < b) //枚举完这个月后,如果星期c出现的次数小于b,说明没有第b个星期c,输出none
{
puts("none");
}
}
days += get_days(year, month); //这个月过完之后加上这个月过的天数
}
return 0;
} 第四题:网络延时
给定一个公司的网络,由 n 台交换机和 m 台终端电脑组成,交换机与交换机、交换机与电脑之间使用网络连接。
交换机按层级设置,编号为 1 的交换机为根交换机,层级为 1。
其他的交换机都连接到一台比自己上一层的交换机上,其层级为对应交换机的层级加 1。
所有的终端电脑都直接连接到交换机上。
当信息在电脑、交换机之间传递时,每一步只能通过自己传递到自己所连接的另一台电脑或交换机。
请问,电脑与电脑之间传递消息、或者电脑与交换机之间传递消息、或者交换机与交换机之间传递消息最多需要多少步。
输入格式
输入的第一行包含两个整数 n,m,分别表示交换机的台数和终端电脑的台数。
第二行包含 n−1 个整数,分别表示第 2、3、……、n 台交换机所连接的比自己上一层的交换机的编号。第 i 台交换机所连接的上一层的交换机编号一定比自己的编号小。
第三行包含 m 个整数,分别表示第 1、2、……、m 台终端电脑所连接的交换机的编号。
输出格式
输出一个整数,表示消息传递最多需要的步数。
数据范围
前 30% 的评测用例满足:n≤5,m≤5。
前 50% 的评测用例满足:n≤20,m≤20。
前 70% 的评测用例满足:n≤100,m≤100。
所有评测用例都满足:1≤n≤10000,1≤m≤10000。输入样例1:
4 2 1 1 3 2 1输出样例1:
4样例1解释
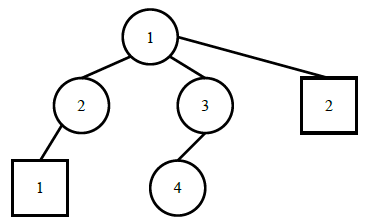
样例的网络连接模式如下,其中圆圈表示交换机,方框表示电脑:
其中电脑 1 与交换机 4 之间的消息传递花费的时间最长,为 4 个单位时间。
输入样例2:
4 4 1 2 2 3 4 4 4输出样例2:
4样例2解释
样例的网络连接模式如下:
其中电脑 1 与电脑 4 之间的消息传递花费的时间最长,为 4 个单位时间。
解题思路:经典的树的直径的题目(还是看了模板才写出来)不多解释了直接上代码
以下是代码:
c++
#include
#include
#include
using namespace std;
const int N = 1e5 + 10 , INF = 0x3f3f3f3f3f;
int n , m;
int h[N] , ne[N] , e[N] , idx;
int res;
void add(int a , int b)
{
e[idx] = b , ne[idx] = h[a] , h[a] = idx ++;
}
void floyd(int dist[][10])
{
// 显然超时的方法
for(int k = 1;k <= n + m;k ++)
for(int i = 1;i <= n + m;i ++)
for(int j = 1;j <= n + m;j ++)
dist[i][j] = min(dist[i][j] , dist[i][k] + dist[k][j]);
}
int dfs(int u)
{
int d1 = 0 , d2 = 0; // d1记录u到最远叶节点的距离,d2记录u到次远叶节点的距离
for(int i = h[u];i != -1;i = ne[i])
{
int j = e[i];
int d = dfs(j); // 求子节点j到最远叶节点的距离
if(d >= d1) d2 = d1 , d1 = d;
else if(d > d2) d2 = d;
}
res = max(res , d1 + d2);
return d1 + 1;
}
int main()
{
memset(h , -1 , sizeof h);
cin >> n >> m;
for(int i = 2;i <= n;i ++)
{
int x;
cin >> x;
// x和i建立边
add(x , i);
}
for(int j = n + 1;j <= n + m;j ++)
{
int x;
cin >> x;
// x和i建立边
add(x , j);
}
dfs(1);
cout << res << endl;
return 0;
} 第五题:最小花费
C 国共有 n 个城市,编号 1∼n。
有 n−1 条双向道路,每条道路连接两个城市,任意两个城市之间能互相到达。
小 R 来到 C 国旅行,他共规划了 m 条旅行的路线,第 i 条旅行路线的起点是 si,终点是 ti。
在旅行过程中,小 R 每行走一单位长度的路需要吃一单位的食物。
C 国的食物只能在各个城市中买到,而且不同城市的食物价格可能不同。
然而,小 R 不希望在旅行中为了购买较低价的粮食而绕远路,因此他总会选择最近的路走。
现在,请你计算小 R 规划的每条旅行路线的最小花费是多少。
输入格式
第一行包含 2 个整数 n 和 m。
第二行包含 n 个整数。第 i 个整数 wi 表示城市 i 的食物价格。
接下来 n−1 行,每行包括 3 个整数 u,v,e,表示城市 u 和城市 v 之间有一条长为 e 的双向道路。
接下来 m 行,每行包含 2 个整数 si 和 ti,分别表示一条旅行路线的起点和终点。
输出格式
输出 m 行,分别代表每一条旅行方案的最小花费。
数据范围
前 10% 的评测用例满足:n,m≤20,wi≤20;
前 30% 的评测用例满足:n,m≤200;
另有 40% 的评测用例满足:一个城市至多与其它两个城市相连。
所有评测用例都满足:1≤n,m≤1e5,1≤wi≤1e6,1≤e≤10000。输入样例:
6 4 1 7 3 2 5 6 1 2 4 1 3 5 2 4 1 3 5 2 3 6 1 2 5 4 6 6 4 5 6输出样例:
35 16 26 13样例解释
对于第一条路线,小 R 会经过 2→1→3→5。
其中在城市 2 处以 7 的价格购买 4 单位粮食,到城市 1 时全部吃完,并用 1 的价格购买 7 单位粮食,然后到达终点。
解题思路:不会(学习代码)
以下是代码:
c++
#include
#include
#include
#include
#define x first
#define y second
using namespace std;
typedef long long LL;
typedef pair PII;
const int N = 100010, M = N * 2, INF = 0x3f3f3f3f;
int n, m;
int pr[N];
int h[N], e[M], w[M], ne[M], idx;
bool st[N];
struct Query
{
int a, b;
LL c;
}query[N];
vector Q[N];
int bel[N];
int fp[N][17], fu[N][17], dist[N], cm[N];
LL cs[N];
vector qt[N];
LL cs2[N];
int minp[N], minu[N], top;
void add(int a, int b, int c)
{
e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}
int get_size(int u, int fa) // 求子树大小
{
if (st[u]) return 0;
int res = 1;
for (int i = h[u]; ~i; i = ne[i])
if (e[i] != fa)
res += get_size(e[i], u);
return res;
}
int get_wc(int u, int fa, int tot, int& wc) // 求重心
{
if (st[u]) return 0;
int sum = 1, ms = 0;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j == fa) continue;
int t = get_wc(j, u, tot, wc);
ms = max(ms, t);
sum += t;
}
ms = max(ms, tot - sum);
if (ms <= tot / 2) wc = u;
return sum;
}
void dfs1(int u, int fa, int id)
{
if (st[u]) return;
bel[u] = id, qt[u].clear();
fp[u][0] = fa, fu[u][0] = u;
for (int i = 1; i < 17; i ++ )
{
int p = fp[u][i - 1];
fp[u][i] = fp[p][i - 1];
if (pr[fu[u][i - 1]] <= pr[fu[p][i - 1]]) fu[u][i] = fu[u][i - 1];
else fu[u][i] = fu[p][i - 1];
}
if (pr[fu[u][16]] == pr[u]) // 最小的是自己
{
cs[u] = (LL)dist[u] * pr[u];
cm[u] = pr[u];
}
else
{
int x = u;
for (int i = 16; i; i -- )
if (pr[fu[x][i - 1]] >= pr[u])
x = fp[x][i - 1];
cs[u] = (LL)(dist[u] - dist[x]) * pr[u] + cs[x];
cm[u] = cm[x];
}
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j != fa && !st[j])
{
dist[j] = dist[u] + w[i];
dfs1(j, u, id);
}
}
}
void dfs2(int u, int fa)
{
if (st[u]) return;
if (minp[top - 1] < pr[u]) minp[top] = minp[top - 1], minu[top] = minu[top - 1];
else minp[top] = pr[u], minu[top] = u;
top ++ ;
for (int i = 0; i < qt[u].size(); i ++ )
{
int a = qt[u][i].x, k = qt[u][i].y;
if (cm[a] <= minp[top - 1]) query[k].c = cs[a] + (LL)dist[u] * cm[a];
else
{
int l = 0, r = top - 1;
while (l < r)
{
int mid = l + r >> 1;
if (minp[mid] < cm[a]) r = mid;
else l = mid + 1;
}
int ver = minu[r];
query[k].c = cs[a] + cs2[u] - cs2[ver] + (LL)dist[ver] * cm[a];
}
}
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (j != fa && !st[j])
{
cs2[j] = cs2[u] + (LL)minp[top - 1] * w[i];
dfs2(j, u);
}
}
top -- ;
}
void calc(int u)
{
if (st[u]) return;
vector q;
q.swap(Q[u]);
get_wc(u, -1, get_size(u, -1), u);
st[u] = true; // 删除重心
for (int i = 0; i < 17; i ++ ) fp[u][i] = 0, fu[u][i] = u;
dist[u] = cs[u] = 0, cm[u] = pr[u], bel[u] = 0, qt[u].clear();
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
dist[j] = dist[u] + w[i];
dfs1(j, u, j);
}
for (int i = 0; i < q.size(); i ++ )
{
int k = q[i];
int a = query[k].a, b = query[k].b;
if (b == u) query[k].c = cs[a];
else if (bel[a] == bel[b]) Q[bel[a]].push_back(k);
else qt[b].push_back({a, k});
}
cs2[u] = 0, minp[0] = pr[u], minu[0] = u, top = 1;
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
cs2[j] = cs2[u] + (LL)minp[top - 1] * w[i];
dfs2(j, u);
}
for (int i = h[u]; ~i; i = ne[i])
{
int j = e[i];
if (Q[j].size()) calc(j);
}
}
int main()
{
scanf("%d%d", &n, &m);
pr[0] = INF;
for (int i = 1; i <= n; i ++ ) scanf("%d", &pr[i]);
memset(h, -1, sizeof h);
for (int i = 0; i < n - 1; i ++ )
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c), add(b, a, c);
}
for (int i = 0; i < m; i ++ )
{
int a, b;
scanf("%d%d", &a, &b);
query[i] = {a, b};
if (a != b) Q[1].push_back(i);
}
calc(1);
for (int i = 0; i < m; i ++ )
printf("%lld\n", query[i].c);
return 0;
}