【C++刷题集】-- day4
目录
选择题
单选
编程题
计算糖果⭐
【题目解析】
【解题思路】
进制转换⭐
【题目解析】
【解题思路】
选择题
单选
#include
#include
using namespace std;
int main() {
int m = 0123, n = 123;
printf("%o %o\n", m, n);
return 0;
}
解析:
转换说明符 转换说明符 描述 %d有符号十进制整数 %i有符号十进制整数 %u无符号十进制整数 %o八进制整数 %x十六进制整数(小写字母) %X十六进制整数(大写字母) %f浮点数 %e用科学计数法表示的浮点数(小写字母e) %E用科学计数法表示的浮点数(大写字母E) %g根据数值的大小自动选择 %f或%e格式%G根据数值的大小自动选择 %f或%E格式%c单个字符 %s字符串 %p指针地址 %n将已打印字符数保存在整型指针中 %%打印一个百分号 本题中:
- m为前缀0 -> 八进制。
- n为无前后缀 -> 十进制。
所以根据八进制输出,就是123与173(8^2 * 1 + 8^1 * 7 + 8^0 * 3 = 123)。
----------------------------------------------
解析:
位操作符 名称 功能 & 按位与 将两个操作数的每一位进行比较,如果两个操作数的对应位都为1,则该位结果为1,否则为0。 | 按位或 将两个操作数的每一位进行比较,如果两个操作数的对应位都为0,则该位结果为0,否则为1。 ^ 按位异或 将两个操作数的每一位进行比较,如果两个操作数的对应位相同,则该位结果为0,否则为1。 ~ 按位取反 将一个二进制数的每一位取反(0变成1,1变成0)。 左移 << 将一个二进制数向左移动指定的位置。左侧空出来的位置用0填充。 右移 >> 将一个二进制数向右移动指定的位置。右侧空出来的位置用0填充(如果原始数字是正数),或者用1填充(如果原始数字是负数)。 #includeusing namespace std; int main() { unsigned int a = 60; // 0011 1100 unsigned int b = 13; // 0000 1101 int result = 0; result = a & b; // 0000 1100 cout << "a & b = " << result << endl; result = a | b; // 0011 1101 cout << "a | b = " << result << endl; result = a ^ b; // 0011 0001 cout << "a ^ b = " << result << endl; result = ~a; // 1100 0011 cout << "~a = " << result << endl; result = a << 2; // 1111 0000 cout << "a << 2 = " << result << endl; result = a >> 2; // 0000 1111 cout << "a >> 2 = " << result << endl; return 0; } // 输出: a & b = 12 a | b = 61 a ^ b = 49 ~a = -61 a << 2 = 240 a >> 2 = 15对于比特位设为0 / 1对应的位运算是:
#includeusing namespace std; int main() { int flag = 5; // 5:二进制表示为101b cout << "flag: " << flag << endl; // 将第二个bit置0 flag &= ~2; // 2:二进制表示为10b cout << "flag after clearing bit 2: " << flag << endl; // 将第二个bit置1 flag |= 2; // 2:二进制表示为10b cout << "flag after setting bit 2: " << flag << endl; return 0; }
----------------------------------------------
解析:
const修饰指针的关键:
- const在*前:const修饰的是解引用的结果不能修改,即指向的执行空间中的内容不能修改。
- const在*后:const修饰指针变量本身,即指针的值不能修改,指针的指向不能修改。
题目选项:
- const int * const x = &y; 这个声明表示 x 是一个指向常量整数的指针,同时也是一个常量指针,即该指针所指向的内存地址和内存中的值都不能被修改。
- int * const x = &y; 这个声明表示 x 是一个指向整数的常量指针,即该指针所指向的内存地址不能被修改,但内存中的值可以被修改。
- const int * x = &y; 这个声明表示 x 是一个指向常量整数的指针,即该指针所指向的内存地址不能被修改,但内存中的值可以被修改。
- int const * x = &y; 这个声明和第三种声明等价,即x也是一个指向常量整数的指针。
- const int * const x = &y; 这个声明表示 x 是一个既是常量又是常量指针的变量,即该变量所指向的内存地址和内存中的值都不能被修改。
----------------------------------------------
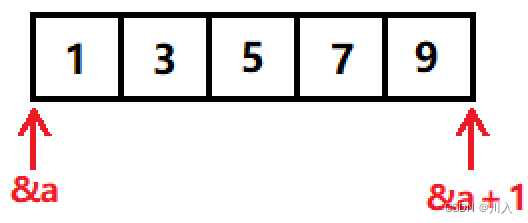
int a[5] = { 1,3,5,7,9 };
int* p = (int*)(&a + 1);
printf("% d, % d", *(a + 1),* (p - 1));运行结果是什么?
解析:
考察核心:数组名只有在 & 和 sizeof 之后,才表明数组本身,其余都表示首元素的地址。
- int a[5] = {1,3,5,7,9}; 定义了一个长度为5的整型数组a,并初始化。
- int* p = (int*)(&a +1); 定义了一个指向整型数据类型的指针 p(int(*)[5]),将 p 的地址 + 1,即指向了 a[4] 后面的地址。
- printf("%d,%d", *(a+1),*(p-1)); 输出 a[1] 和 p[-1] 所指向的值,即3和9。其中*(a+1)等价于a[1],*(p-1)等价于p[-1]。
----------------------------------------------
解析:
不知道有多少行,每行有多少列。假设:数组X的起始地址为start,总共有M行和N列。
- &X[4][4] = start + 4*N + 4 = 0xf8b82140
- &X[9][9] = start + 9*N + 9 = 0xf8b8221c
- &X[7][7] = start + 7*N + 7
在这个时候我们就可以发现,就是简单的二元一次方程了,但是还是很难进行计算,所起其实这里我们还需要进行题目关键点的提取,用以进行进一步的简化运算。
- &X[4][4] = 0xf8b82140 -> &X[4][9] = 0xf8b82145
- 而 X[4][9] 和 X[9][9] 之间刚相隔了 5 行:0xf8b8221c - 0xf8b82145 = 5*N
于是:0x21c - 0x145 = 0xD7 -> N = 43。
- &X[7][7] = &X[7][9] - 2
- &X[7][9] = X[4][9] + 3*43
最后:&X[7][7] = Oxf8b821c4
----------------------------------------------
#include
using namespace std;
void func(char** m) {
++m;
cout << *m << endl;
}
int main() {
static char* a[] = { "morning", "afternoon", "evening" };
char** p;
p = a;
func(p);
return 0;
}
解析:
考察核心:数组名只有在 & 和 sizeof 之后,才表明数组本身,其余都表示首元素的地址。
此处是 p = a,就是a的首元素的地址,而该数组的首元素 "moring" 类型为char*,所以 p 就需要给成二级指针。
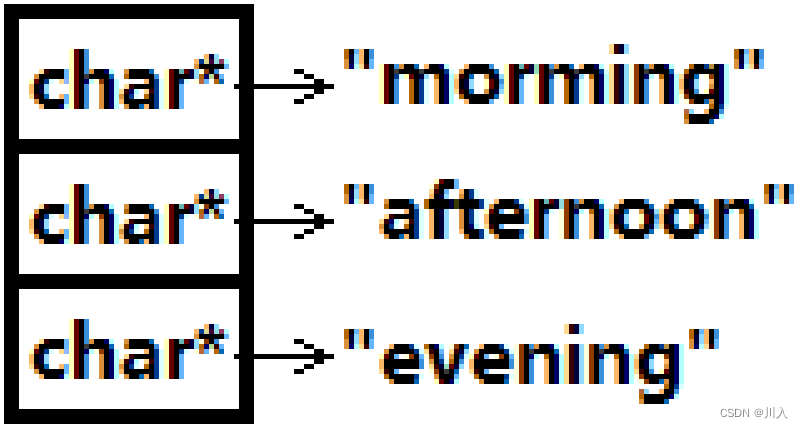
于是将p传给m,所以m指向首元素 "moring",随后前置++。也就是让这个指针向后偏移一个元素的大小,便是下一个元素 "afternoon" 。
数组 a 的格式可以想象为如下:
----------------------------------------------
int func(int x) {
int count = 0;
while (x)
{
count++;
x = x & (x - 1);//与运算
}
return count;
}
解析:
假设 x = 7 -> 111
- 第一次循环:count++ -> count = 1,x = 7&6 = 111&110 = 110,x = 6。
- 第二次循环:count++ -> count = 2,x = 6&5 = 110&101 = 100,x = 4。
- 第三次循环:count++ -> count = 3,x = 4&3 = 100&011 = 0,x = 0。
最终放回的就是3。
#注:这个算法的功能就是,返回x中总共有多少个1。
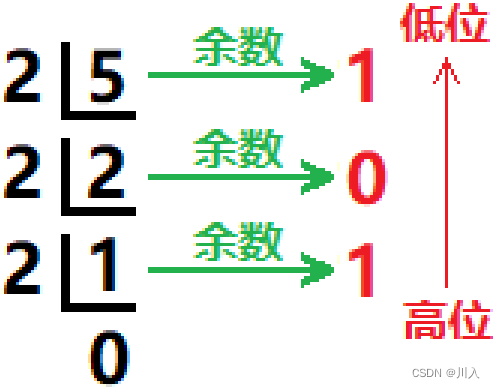
于是接下就是将9999转换为二进制就可以了,10011100001111b,有8个零。
计算方式此处以5举例:
----------------------------------------------
#include
int cnt = 0;
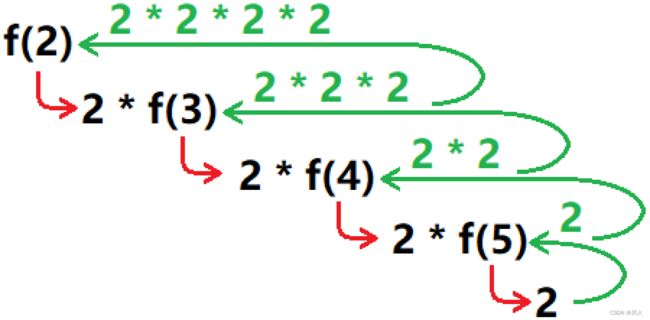
int fib(int n) {
cnt++;
if (n == 0)
return 1;
else if (n == 1)
return 2;
else
return fib(n - 1) + fib(n - 2);
}
void main() {
fib(8);
printf("%d", cnt);
} struct A
{
int a;
short b;
int c;
char d;
};
struct B
{
int a;
short b;
char c;
int d;
};
解析:
结构体的大小计算遵循结构体的对齐规则:
结构体的第一个成员放在结构体变量在内存中存储位置的0偏移处开始
从第2个成员往后的所有成员,都要放在一个对齐数(成员的大小和默认对齐数的较小值)的整数的整数倍的地址处,VS中默认对齐数为8
结构体的总大小是结构体的所有成员的对齐数中最大对齐数的整数倍。
如果嵌套了结构体的情况,嵌套的结构体对齐到自己的最大对齐数的整数倍处,结构体的整体大小就是所有最大对齐数(含嵌套结构体的对齐数)的整数倍
#注:VS中的默认对齐数为8,不是所有编译器都有默认对齐数,当编译器没有默认对齐数的时候,成员变量的大小就是该成员的对齐数。(Linux中就没有默认对齐数概念)
补充:
#结构体为什么要内存对齐?
- 平台原因(移植原因):
- 不是所有的硬件平台都能访问任意地址上的任意数据的;某些硬件平台只能在某些地址处取某些特定类型的数据,否则抛出硬件异常。
- 性能原因:
- 数据结构(尤其是栈)应该尽可能地在自然边界上对齐。原因在于,为了访问未对齐的内存,处理器需要作两次内存访问;而对齐的内存访问仅需要一次访问。
总体来说:结构体的内存对齐是拿空间来换取时间的做法。
----------------------------------------------
编程题
计算糖果⭐
计算糖果_牛客题霸_牛客网 (nowcoder.com)
【题目解析】
【解题思路】
- A - B、B - C、A + B、B + C 这道题目的实质是:判断三元一次方程组是否有解及求解。
- 最后需要判断一下逆推是否成立。
#include
#include
using namespace std;
// 判断糖果数是否合理
inline bool judge_no(float num)
{
if(num < 0 || (int)num < num)
return true;
return false;
}
int main() {
vector val(5, 0);
for(int i = 1; i < 5; i++)
{
int number = 0;
cin >> number;
val[i] = number;
}
float A = (val[1] + val[3]) / 2.0;
if(judge_no(A))
{
cout << "No" << endl;
return 0;
}
float B = val[3] - A;
if(judge_no(B))
{
cout << "No" << endl;
return 0;
}
float C = val[4] - B;
if(judge_no(C))
{
cout << "No" << endl;
return 0;
}
// 反推合理性
if(A - B != val[1] ||
B - C != val[2] ||
A + B != val[3] ||
B + C != val[4])
{
cout << "No" << endl;
return 0;
}
printf("%d %d %d", (int)A, (int)B ,(int)C);
return 0;
} 进制转换⭐
进制转换_牛客题霸_牛客网 (nowcoder.com)
【题目解析】
#include
#include
#include
using namespace std;
int main() {
const char* table = "0123456789ABCDEF";
int m, n;
cin >> m >> n;
bool flag = false;
// 如果是负数,则转成正数,并标记一下
if (m < 0)
{
m = 0 - m;
flag = true;
}
// 按进制换算成对应的字符添加到ret
string ret;
while (m)
{
ret += table[m % n];
m /= n;
}
if (flag)
ret += '-';
if(ret.empty())
ret += table[0];
auto rit = ret.rbegin();
while(rit != ret.rend())
cout << *rit++;;
cout << endl;
return 0;
}